
3)运动方程和轨道方程 、质点在运动过程中,空间位置随时间变化的函数式称为运 动方程。 表示为:x=x() y=y(1),(1). 或 r=(t) 运动方程是时间的显函数。 b、质点在空间所经过的路径称为轨道(轨迹)。 从上式中消去即可得到轨道方程。 轨道方程不是时间显函数。 首页上页下页退出
首 页 上 页 下 页 退 出 11 3)运动方程和轨道方程 表示为: x = x(t) , y = y(t) , z = z(t). 或 r r(t) = 运动方程是时间t的显函数。 a、质点在运动过程中,空间位置随时间变化的函数式称为运 动方程。 b、质点在空间所经过的路径称为轨道(轨迹)。 从上式中消去t即可得到轨道方程。 轨道方程不是时间t显函数

2、位移和路程 1)位移△广 a、定义:由起始位置指向终了位置的有向线段; △t时间内位置矢量的增量 △r=店-方 w==-l 位移的模△与矢量模的增量△”不是同一个量 |△W月5-F=V6x2-x}+0y2-y}+(2-} w店|-|所卡√x号+号+2号-√x2++z 首页上页下页退出
首 页 上 页 下 页 退 出 12 2、位移和路程 1)位移 r a、定义 :由起始位置指向终了位置的有向线段; 2 1 r r r △t 时间内位置矢量的增量 = − r 位移的模 与矢量模的增量 r 不是同一个量 | | | | 2 1 r r r = − | | | | 2 1 r r r = − X Y Z 1 r 2 r r A B S 1 r 2 r r A B 1 r 2 2 1 r r r r = = − ( ) ( ) ( ) 2 2 1 2 2 1 2 2 1 = x − x + y − y + z − z 2 1 2 1 2 1 2 2 2 2 2 2 = x + y + z − x + y + z
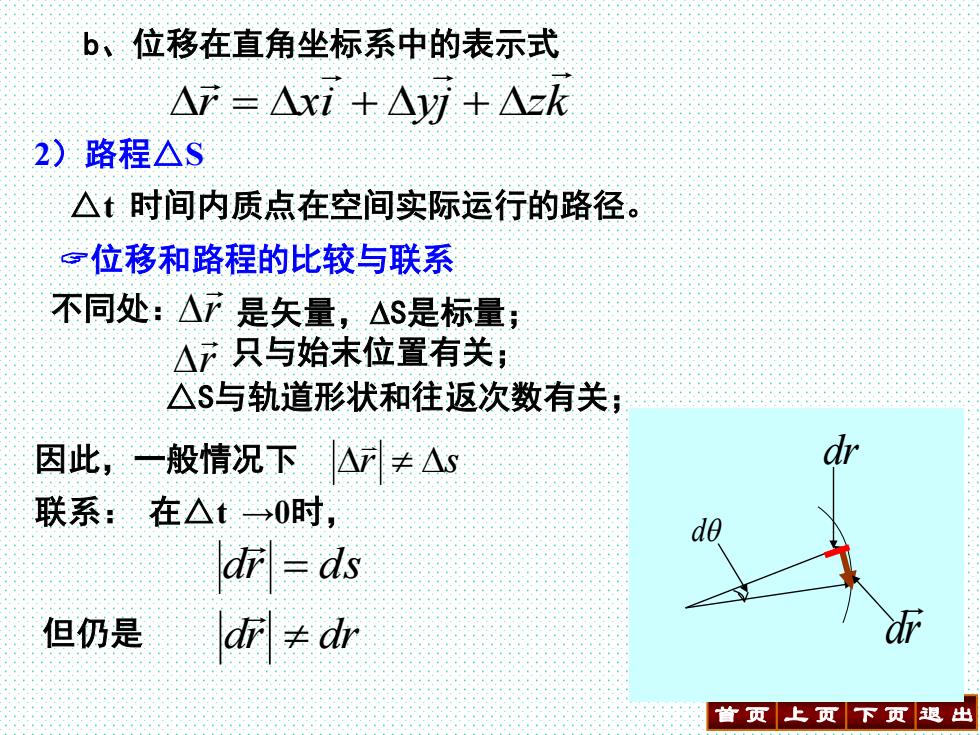
b、位移在直角坐标系中的表示式 △F=△xi+△以+△zk 2)路程△S △t时间内质点在空间实际运行的路径。 一位移和路程的比较与联系 不同处:△下是矢量,△S是标量; △7只与始未位置有关; △$与轨道形状和往返次数有关; 因此,一般情况下]△≠△s 联系:在△t →0时, de dr =ds 但仍是 d≠dr 首页上页下页退出
首 页 上 页 下 页 退 出 13 b、位移在直角坐标系中的表示式 r xi yj zk = + + 2)路程△S 位移和路程的比较与联系 联系: 在△t →0时, dr = ds dr dr △t 时间内质点在空间实际运行的路径。 不同处: r 只与始末位置有关; △S与轨道形状和往返次数有关; r s 因此,一般情况下 r 是矢量,S是标量; 但仍是 d dr dr

3、速度 描述质点位置变化和方向变化快慢的物理量 1)平均速度与平均速率 = =4s △t △t 读成时刻附近△时间内的平均速度(或速率) 币=vto y 4 首页上页下页退出
首 页 上 页 下 页 退 出 14 3、速 度 1)平均速度与平均速率 t r v = t s v = 读成t时刻附近△t时间内的平均速度(或速率) z A 0 0 v = v B 1 r 2 r 3 r 0 y x 1 r 2 r 描述质点位置变化和方向变化快慢的物理量

在一般情况下 同≠下 在直角坐标系中 2)瞬时速度与瞬时速率 下=im 可见速度是位矢对时间的变化率。 At→0△1 dt v=lim As dt 可见速率是路程对时间的变化率。 At-→0△1 = ds =y 可见速率是速度的模。 dt .V=VTo 0是轨道切线方向上的单位矢。 首页上页下页退出
首 页 上 页 下 页 退 出 15 2)瞬时速度与瞬时速率 dt dr t r t v = → = 0 lim dt ds t s t v = → = 0 lim v dt ds dt dr v = = = 0 v = v v v 在一般情况下 k t z j t y i t x v + + 在直角坐标系中 = 0 是轨道切线方向上的单位矢。 可见速度是位矢对时间的变化率。 可见速率是速度的模。 可见速率是路程对时间的变化率