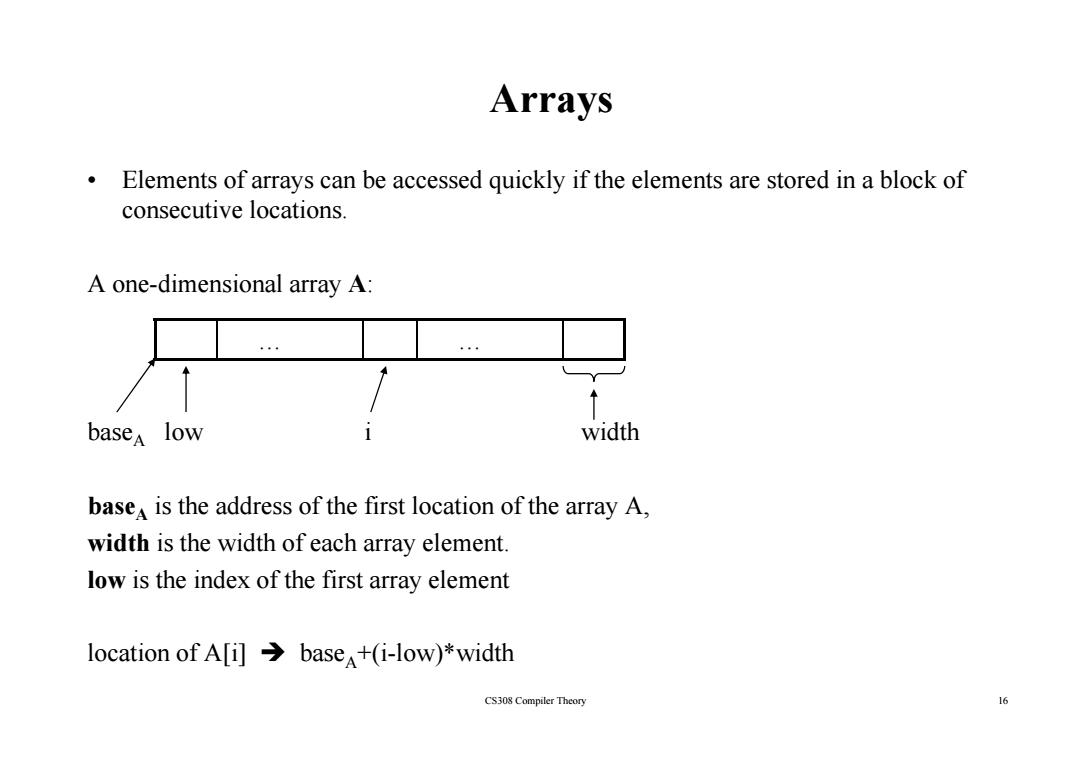
Arrays Elements of arrays can be accessed quickly if the elements are stored in a block of consecutive locations. A one-dimensional array A: basea low width base is the address of the first location of the array A, width is the width of each array element. low is the index of the first array element location of A[i]>base+(i-low)*width CS308 Compiler Theory 16
Arrays • Elements of arrays can be accessed quickly if the elements are stored in a block of consecutive locations consecutive locations. A one-dimensional array A: … … baseA low i width baseA is the address of the first location of the array A, width is the width of each array element. low is the index of the first array element CS308 Compiler Theory 16 location of A[i] Î baseA+(i-low)*width

Arrays (cont.) base+(i-low)*width can be re-written as i*width (basea-low*width) should be computed at run-time can be computed at compile-time o So,the location of A[i]can be computed at the run-time by evaluating the formula i*width+c where c is(base-low*width)which is evaluated at compile-time. Intermediate code generator should produce the code to evaluate this formula i*width+c (one multiplication and one addition operation). CS308 Compiler Theory
Arrays (cont.) baseA+(i-low)*width can be re-written as i*width + (baseA-low*width) should be computed at run-time can be computed at compile-time • So, the location of A[i] can be computed at the run-time by evaluating the formula i*width+c where c is (baseA-low*width) which is evaluated at compile-time. • Intermediate code generator should produce the code to evaluate this formula i*width+c (one multiplication and one addition operation). CS308 Compiler Theory 17

Two-Dimensional Arrays A two-dimensional array can be stored in -either row-major (row-by-row)or column-major (column-by-column). Most of the programming languages use row-major method. Row-major representation of a two-dimensional array: roWj row2 rown CS308 Compiler Theory 18
Two-Dimensional Arrays • A two-dimensional array can be stored in – either row-major (row-by-row) or – column-major (column-by-column). • Most of the programming languages use row-major method. • Row-major representation of a two-dimensional array: row1 row 2 row n CS308 Compiler Theory 18

Two-Dimensional Arrays (cont.) .The location of A[iji]is base+((i-low)*n2+i2-low2)*width base is the location of the array A. low is the index of the first row lowz is the index of the first column nz is the number of elements in each row width is the width of each array element Again,this formula can be re-written as ((i1*n2)+i)*width +(baseA-((low1*n)+low2)*width) should be computed at run-time can be computed at compile-time CS308 Compiler Theory 19
Two-Dimensional Arrays (cont.) • The location of A[i1,i 2] is base A+ ((i1-low1)*n 2+i 2-low 2)*width base A is the location of the array A is the location of the array A. low 1 is the index of the first row low 2 is the index of the first column n 2 is the number of elements in each row width is the width of each arra y element • Again, this formula can be re-written as ((i * )+i )* idth + (b ((l * )+l )* idth) 1* n 2)+i 2)* width + (base A -((low1* n1)+low 2)* width) should be computed at run time can be computed at compile time CS308 Compiler Theory 19 should be computed at run -time can be computed at compile -time

Multi-Dimensional Arrays .In general,the location of A[ii2,...i]is ((..((in2)+i)...)*nk+ik)*width (baseA- ((...((low *n)+low)...)*nk+low)*width) So,the intermediate code generator should produce the codes to evaluate the following formula(to find the location of A[i,i2...,i): (.(i*n2十i2).…)*nk+ik)*width+c To evaluate the ((...((in2)+i2)...)*nk+ik portion of this formula,we can use the recurrence equation: e1=l1 em=em-1 nm+im CS308 Compiler Theory 20
Multi-Dimensional Arrays • In general, the location of A[i1,i 2,...,i k] is (( ... ((i1*n 2)+i 2) ...)*n k+i k)*width + (base A - ((...((low1*n1)+low 2)...)*n k+low k)*width) • So, the intermediate code generator should produce the codes to evaluate the following formula (to find the location of A[i evaluate the following formula (to find the location of A[i i i ]) : 1,i 2,..., i k]) : (( ... ((i1*n 2)+i 2) ...)*n k+i k)*width + c • To evaluate the (( ... ((i1*n 2)+i 2) ...)*n k+i k portion of this formula, we can use the recurrence equation: e1 = i1 CS308 Compiler Theory 20 e m = em-1 * n m + i m