15-迷问题(问题描述) 种初始排列 目标排列 1 3 4 15 1 2 3 4 2 5 12 5 6 7 8 7 6 11 14 9 10 11 12 8 9 10 13 13 14 15 通过一系列合法移动将初始排列转换成目标排列。 合法移动:将邻接于空格的牌移动到空格
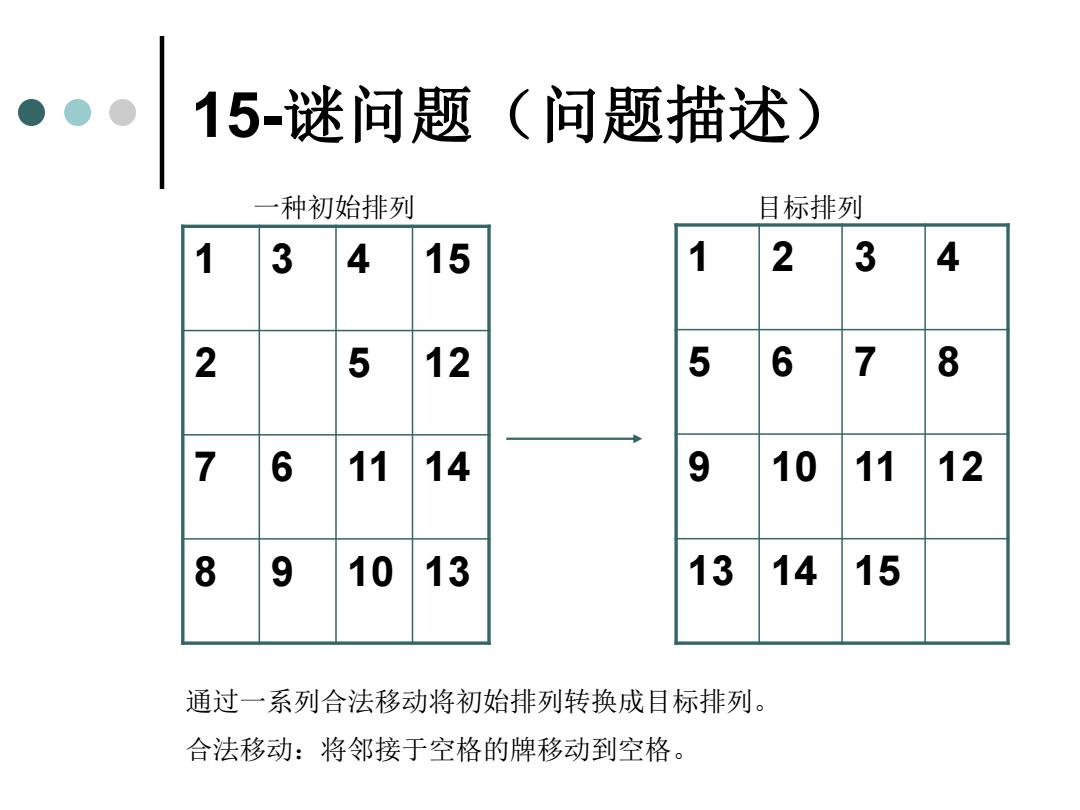
15-谜问题(问题描述) 1 3 4 15 2 5 12 7 6 11 14 8 9 10 13 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 通过一系列合法移动将初始排列转换成目标排列。 合法移动:将邻接于空格的牌移动到空格。 一种初始排列 目标排列

15-迷问题(是否有解) 。棋盘存在16!种不同排列 。任一初始状态,可到达的状态为这些 排列中的一半 。在求解问题前,需要判定目标状态是 否在初始状态的状态空间中
15-谜问题(是否有解) 棋盘存在16!种不同排列 任一初始状态,可到达的状态为这些 排列中的一半 在求解问题前,需要判定目标状态是 否在初始状态的状态空间中

15-谜问题(判定方法) 。按目标状态给牌编号,空格为16 o h 用POSITION()记录编号为i的牌在初始状 态中的位置;POSITION(16)表示空格 ●图9.2(a)的POSITION ●(15237109131415118161246) o LESS(是使得牌小于牌i且POSITION) >POSITION()的数目 LESS(1)=0;LESS(4)=1;LESS(12)=6
15-谜问题(判定方法) 按目标状态给牌编号,空格为16 用POSITION(i)记录编号为i的牌在初始状 态中的位置; POSITION(16)表示空格 ⚫ 图9.2(a)的POSITION ⚫ (1 5 2 3 7 10 9 13 14 15 11 8 16 12 4 6) LESS(i)是使得牌j小于牌i且POSITION(j) > POSITION(i)的数目 ⚫ LESS(1)=0; LESS(4)=1; LESS(12)=6
15-谜问题(判定方法) 。定理7.1当且仅当 sum(LESS()+X)是偶 数时,目标状态可由此 初始状态到达 X=1:空格恰好在上 图棋盘中的蓝色格子上 X=0:空格在棋盘中 的白色格子上
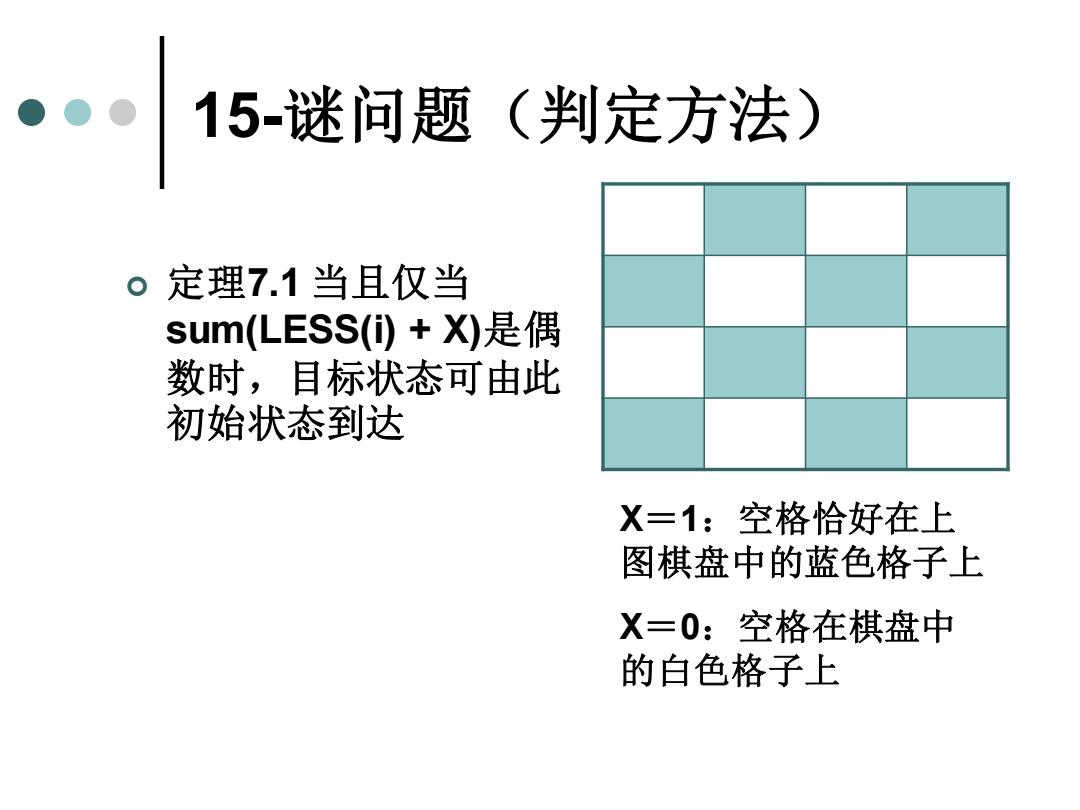
15-谜问题(判定方法) 定理7.1 当且仅当 sum(LESS(i) + X)是偶 数时,目标状态可由此 初始状态到达 X=1:空格恰好在上 图棋盘中的蓝色格子上 X=0:空格在棋盘中 的白色格子上
115-谜问题(宽度优先) 91Q 上 左 右 1234 9101 91071 68 13161512 907红 13141512 左 上 右 左 上 左 -10 13 14 15 1■3 123④23 11 10 910 568 56 13141512 13亚01512 9107▣ 13141512 314512 71 907 13 14 1512 316幼52 36512 下 左 左 16 左 23 12【 56 9的山 910118 1162 13 01512 1316112 115 17 16 20 621 标 910 12
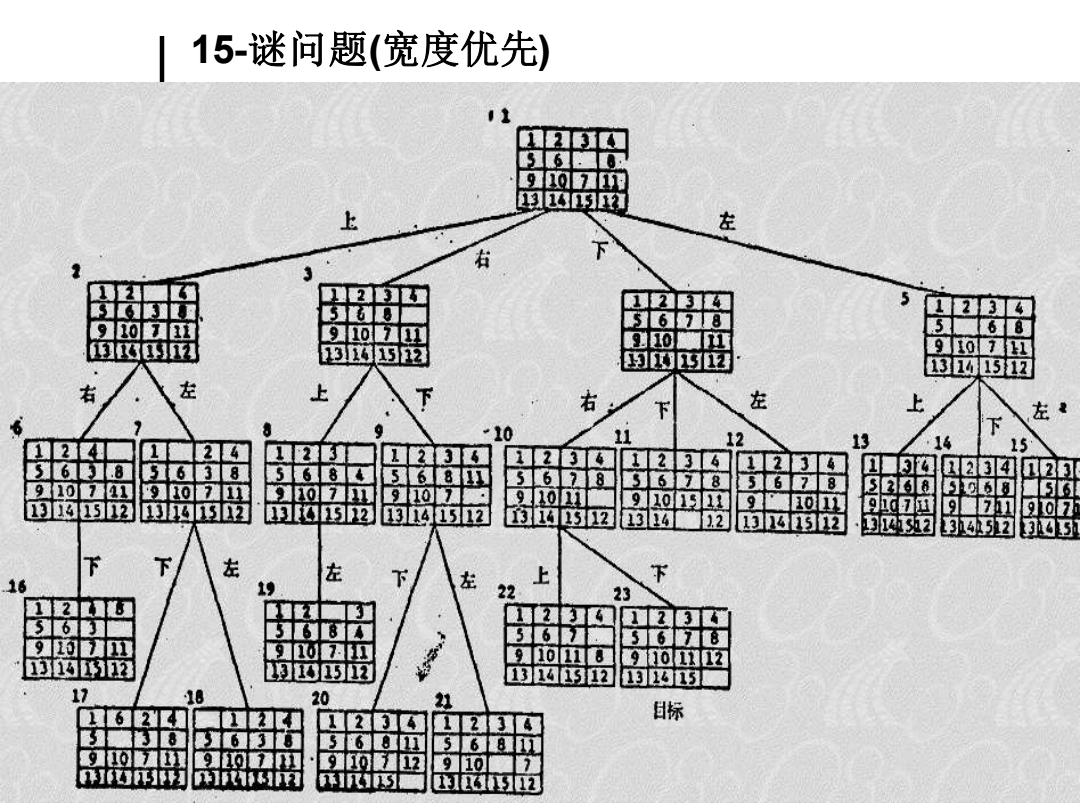
15-谜问题(宽度优先)