
LC-检索(结点成本的两个标 准) 一:在生成一个答案结点之前,子树X需要 生成的结点数。 二:在子树X中离X最近的那个答案结点到X 的路径长度。以图9.1为例 ● 节点1、18和34、29和35、30和38的代价分 别是4,3,2,1 其他2,3,4级上的点代价应分别大于3,2, 1 生成结点(1>2183450>192429>30 32>31)
LC-检索(结点成本的两个标 准) 一:在生成一个答案结点之前,子树X需要 生成的结点数。 二:在子树X中离X最近的那个答案结点到X 的路径长度。以图9.1为例 ⚫ 节点1、18和34、29和35、30和38的代价分 别是4,3,2,1 ⚫ 其他2,3,4级上的点代价应分别大于3,2, 1 ⚫ 生成结点(1>2 18 34 50>19 24 29>30 32>31)
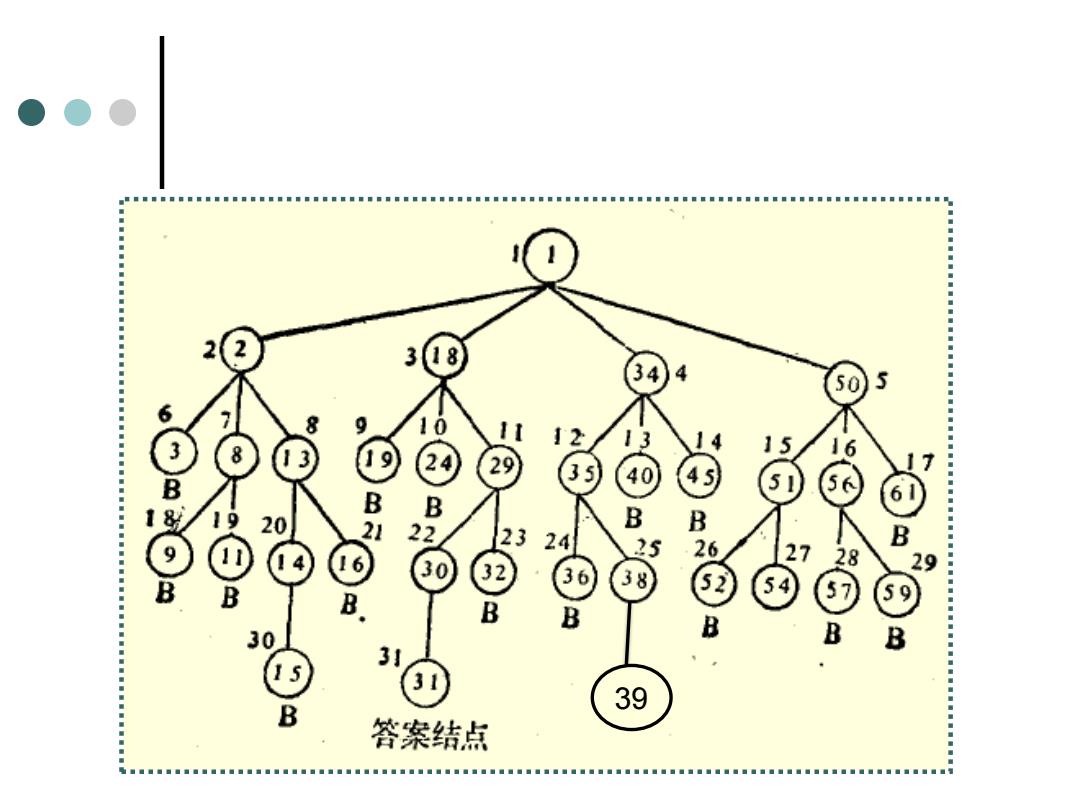
◆ 2 2 3 8 34 4 50 6 8 0 3 1 8 5 3 19 29 3 5 B 40 45 B 9 20 B2 22 B 5 B 9 16 27 30 28 2 6 B 3 38 B 52 5 B B B 30 B B B 3」 15 31 39 B 答案结点
39

·LC-检索(结点成本函数) 0 C()定义 o如果X是答案结点,则CX)是由状态空 间树的根结点到X的成本(即花费的代 价,可以是级数、计算复杂度等) 如果X不是答案结点且子树X不包含任 何答案结点,则C(X)=∞ 。如果X不是答案结点但子树X包含答案 结点,则C)等于子树X中具有最小成 本的答案结点的成本
LC-检索(结点成本函数) C(·)定义 如果X是答案结点,则C(X)是由状态空 间树的根结点到X的成本(即花费的代 价,可以是级数、计算复杂度等) 如果X不是答案结点且子树X不包含任 何答案结点,则C(X)=∞ 如果X不是答案结点但子树X包含答案 结点,则C(X)等于子树X中具有最小成 本的答案结点的成本

LC-检索(成本估计函数) 从前面的两个成本度量标准看,计算C()的工 作量与原问题的解具有相同复杂度。这是因为 计算一个结点的代价通常要检索包含一个答案 结点的子树才能确定,而这正是解决此问题所 要作的检索工作,因此要得到精确的成本函数 一般是不现实的 。因此需要成本估计函数g(X) 0 出现的新问题 仅利用g()会导致算法偏向纵深检查,无法 有效处理下面这种情况:即g(W<g(Z),但Z 比W更接近答案结点
LC-检索(成本估计函数) 从前面的两个成本度量标准看,计算C(·)的工 作量与原问题的解具有相同复杂度。这是因为 计算一个结点的代价通常要检索包含一个答案 结点的子树才能确定,而这正是解决此问题所 要作的检索工作,因此要得到精确的成本函数 一般是不现实的 因此需要成本估计函数g^(X) 出现的新问题 ⚫ 仅利用g^(X) 会导致算法偏向纵深检查,无法 有效处理下面这种情况:即g^(W)<g^(Z),但Z 比W更接近答案结点

LC分枝-限界检索 为使算法不过分偏向于纵深检查,需改进成本 估计函数,使其不只考虑结点X到一个答案结 点的估计成本,还应考虑根节点到结点X的成 本 oc(X)) =f (h(X))+g(X) h()为根结点到结点X的成本 g凶)是由X到达一个答案结点所需做的附加 工作的估计函数 LC-限界检索:选择c()值最小的活结点作为 下一个E结点 BFS:g(X)=0;f(h(X)) =X的级数 D-Search:f(h(X)=0;每当Y是X的一个儿 子时,总有g(X>=g(Y, oLC分枝-限界检索:伴之有限界函数的LC-检索
LC分枝-限界检索 为使算法不过分偏向于纵深检查,需改进成本 估计函数,使其不只考虑结点X到一个答案结 点的估计成本,还应考虑根节点到结点X的成 本 c^(X) =f (h(X)) + g^(X) h(X)为根结点到结点X的成本 g^(X)是由X到达一个答案结点所需做的附加 工作的估计函数 LC-限界检索:选择c^(·)值最小的活结点作为 下一个E-结点 ⚫ BFS: g^(X)=0; f (h(X)) =X的级数 ⚫ D-Search:f (h(X)) =0;每当Y是X的一个儿 子时,总有g^(X)>=g^(Y), LC分枝-限界检索:伴之有限界函数的LC-检索