
Nelson-Oppen Method (1) 1. Represent all conjuncts in the same DAG f(f(x)-f(y)≠f(z)∧Y≥×∧×≥Y+z∧z≥0 X Z 0 Prof.Necula CS 294-8 Lecture 12 6
Prof. Necula CS 294-8 Lecture 12 6 Nelson-Oppen Method (1) 1. Represent all conjuncts in the same DAG f(f(x) - f(y)) f(z) y x x y + z z 0 f - f f y x z 0 + f

Nelson-Oppen Method (2) 2.Run each sat.procedure Require it to report all contradictions (as usual) Also require it to report all equalities between nodes f Z、 Prof.Necula CS 294-8 Lecture 12 7
Prof. Necula CS 294-8 Lecture 12 7 Nelson-Oppen Method (2) 2. Run each sat. procedure • Require it to report all contradictions (as usual) • Also require it to report all equalities between nodes f - f f y x z 0 + f
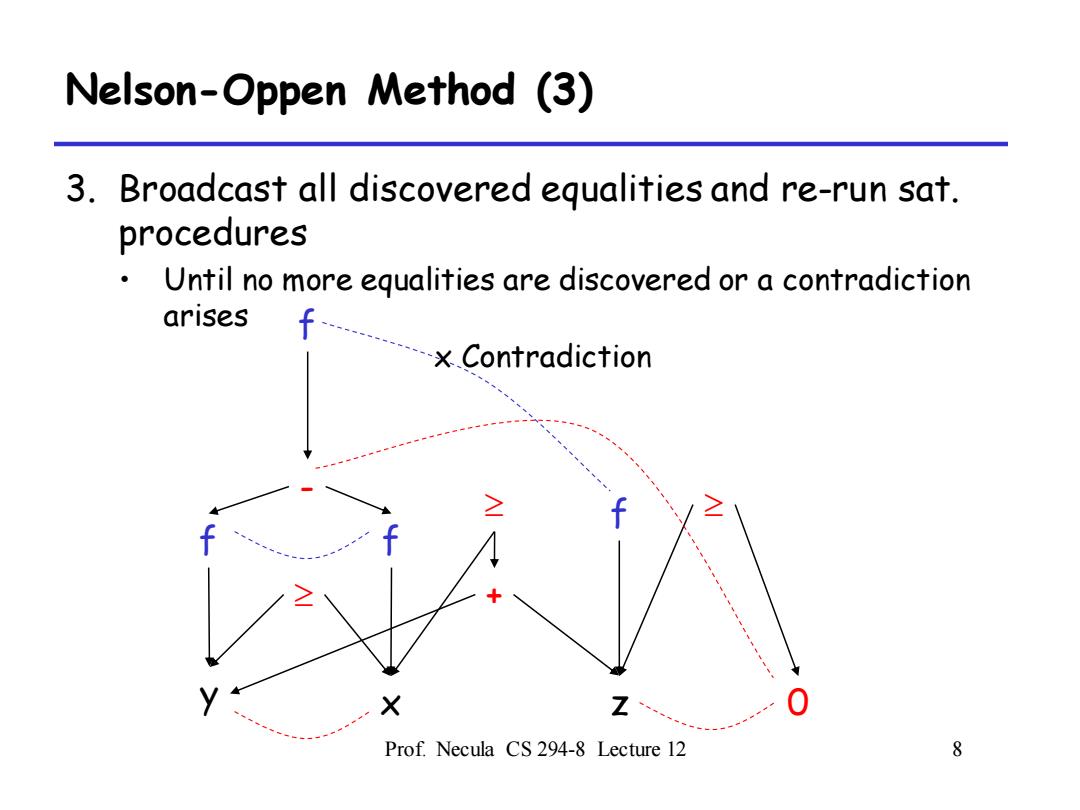
Nelson-Oppen Method (3) 3.Broadcast all discovered equalities and re-run sat. procedures Until no more equalities are discovered or a contradiction arises f x Contradiction Z、 Prof.Necula CS 294-8 Lecture 12 8
Prof. Necula CS 294-8 Lecture 12 8 Nelson-Oppen Method (3) 3. Broadcast all discovered equalities and re-run sat. procedures • Until no more equalities are discovered or a contradiction arises f - f f y x z 0 + f x Contradiction

What Theories Can be Combined? Only theories without common interpreted symbols But Ok if one theory takes the symbol uninterpreted Only certain theories can be combined Consider (Z,+,and Equality -Consider:1≤×≤2Λa=1Ab=2∧f(X)≠f(a)Af(X)≠f(b) No equalities and no contradictions are discovered yet,unsatisfiable A theory is non-convex when a set of literals entails a dis junction of equalities without entailing any single equality Prof.Necula CS 294-8 Lecture 12 9
Prof. Necula CS 294-8 Lecture 12 9 What Theories Can be Combined? • Only theories without common interpreted symbols – But Ok if one theory takes the symbol uninterpreted • Only certain theories can be combined – Consider (Z, +, ·) and Equality – Consider: 1 x 2 a = 1 b = 2 f(x) f(a) f(x) f(b) – No equalities and no contradictions are discovered – Yet, unsatisfiable • A theory is non-convex when a set of literals entails a disjunction of equalities without entailing any single equality

Handling Non-Convex Theories Many theories are non-convex Consider the theory of memory and pointers It is not-convex: trueA=A'v sel(upd(M,A,V),A')=sel(M,A) (neither of the dis juncts is entailed individually) For such theories it can be the case that No contradiction is discovered No single equality is discovered - But a disjunction of equalities is discovered We need to propagate disjunction of equalities.. Prof.Necula CS 294-8 Lecture 12 10
Prof. Necula CS 294-8 Lecture 12 10 Handling Non-Convex Theories • Many theories are non-convex • Consider the theory of memory and pointers – It is not-convex: true A = A’ sel(upd(M, A, V), A’) = sel(M, A’) (neither of the disjuncts is entailed individually) • For such theories it can be the case that – No contradiction is discovered – No single equality is discovered – But a disjunction of equalities is discovered • We need to propagate disjunction of equalities …