
函数举例 ex04_fun_01.cpp #include <iostream> using namespace std; ex04_fun_02.cpp int my_max(int x,int y) 1函数定义,在主调函数前 { if (x y)return x; else return y; int main() { int m,n,p; cout <"please input m and n:" cin >m >n; p=my_max(m,n);/函数调用 cout <<"max("<<m <<","<<n <<")="<<p<<endl; return 0; 7 http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 函数举例 7 #include <iostream> using namespace std; int my_max(int x, int y) // 函数定义,在主调函数前 { if (x > y) return x; else return y; } int main() { int m, n, p; cout << "please input m and n: " ; cin >> m >> n; p = my_max(m,n); // 函数调用 cout << "max(" << m <<"," << n <<")=" << p << endl; return 0; } ex04_fun_01.cpp ex04_fun_02.cpp
函数调用过程 int main() int fun1() int fun3() fun3(); fun1(); fun2(); int fun2() C++程序总是从主函数开始 最后在主函数中结束 8 http://math.ecnu.edu.cn/~jypan
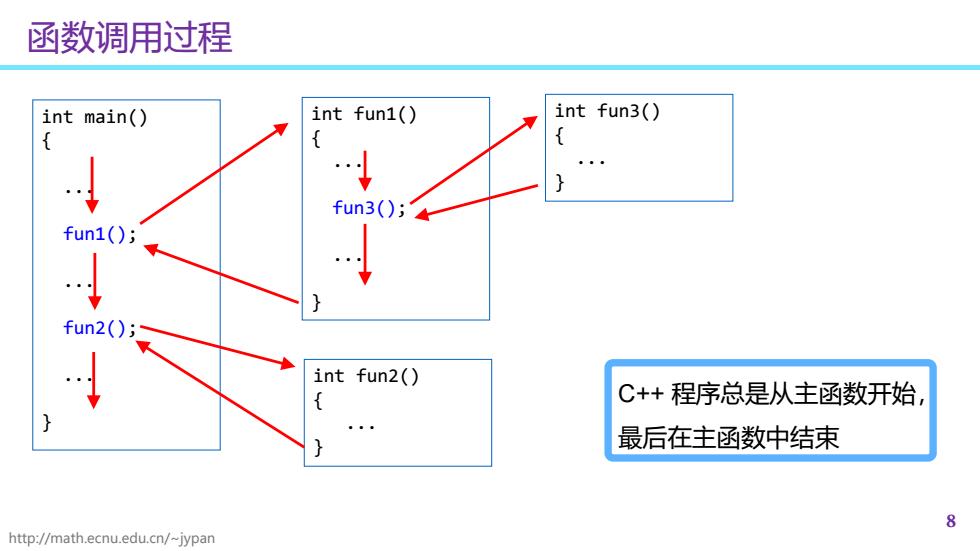
http://math.ecnu.edu.cn/~jypan 函数调用过程 8 int main() { ... fun1(); ... fun2(); ... } int fun1() { ... fun3(); ... } int fun2() { ... } int fun3() { ... } C++ 程序总是从主函数开始, 最后在主函数中结束
函数举例:二进制转十进制 例:编写函数,将一个二进制正整数转化为相应的十进制数 例如:(10101)2=1×24+0×23+1×22+0×21+1×20 分析:需解决两个问题 (1)如何提取每个数位上的数字; (2)如何确定2的次数。 提示:从右往左计算 ex04_bin2dec.cpp 思考 如何提高计算效率:降低计算2k的运算次数 思考 如何计算1111111111111111对应的十进制数?(提示:字符数组) 9 http://math.ecnu.edu.cn/~jypan
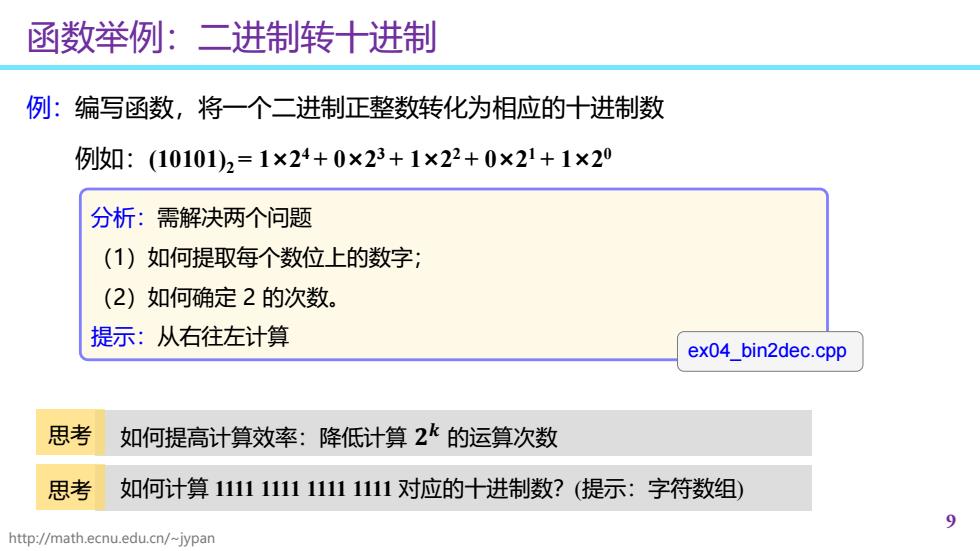
http://math.ecnu.edu.cn/~jypan 函数举例:二进制转十进制 9 例:编写函数,将一个二进制正整数转化为相应的十进制数 例如:(10101)2 = 1×24 + 0×23 + 1×22 + 0×21 + 1×20 分析:需解决两个问题 (1)如何提取每个数位上的数字; (2)如何确定 2 的次数。 提示:从右往左计算 ex04_bin2dec.cpp 思考 如何提高计算效率:降低计算 𝟐𝟐𝒌𝒌 的运算次数 思考 如何计算 1111 1111 1111 1111 对应的十进制数?(提示:字符数组)

函数举例:计算正弦函数值 例:编写函数,利用Taylor展开计算sin(π/2)的近似值 (直到级数某项的绝对值小于1015为止) sin(x)=x 2k+1 1!3+57:+…=) (2k+1)I 分析:注意大数越界和误差累积,简化通项计算方法。 ex04_my_sin.cpp 思考 用上面的方法计算sin (). 结果如何? 10 http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 函数举例:计算正弦函数值 10 例:编写函数,利用 Taylor 展开计算 sin(𝜋𝜋/2) 的近似值 分析:注意大数越界和误差累积,简化通项计算方法。 ex04_my_sin.cpp 用上面的方法计算 sin 41𝜋𝜋 2 思考 ,结果如何? (直到级数某项的绝对值小于 10-15 为止) 3 5 7 2 1 0 sin( ) ( 1) 1! 3! 5! 7! (2 1)! k k k xx x x x x k ∞ + = =− + − += − + ∑

函数举例:回文数 例:找出11~999之间的数m,满足m、m2和m3均为回文数 分析: (1)回文数:各位数字左右对称的整数,如11,121,1331 (2)判别方法:利用除以10取余的方法,从最低位开始,依次取出该数的各位数字。 按反序重新构成新的数,比较与原数是否相等,若相等,则该数为回文数 ex04 huiwen.cpp 11 http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 函数举例:回文数 11 例:找出 11~999 之间的数 m,满足 m、m2 和 m3 均为回文数 分析: (1)回文数:各位数字左右对称的整数,如 11,121,1331 (2)判别方法:利用除以10取余的方法,从最低位开始,依次取出该数的各位数字。 按反序重新构成新的数,比较与原数是否相等,若相等,则该数为回文数 ex04_huiwen.cpp