
9.1优化的主要种类 9.1.7强度削弱和归纳变量删除 和t的值步伐一致地变化 这样的变量叫做归纳变量 =j-1 在循环中有多个归纳变量时, t4=4*j 也许只需要留下一个 ts alt4l 这个操作由归纳变量删除 if ts v goto B3 过程来完成 对本例可以先做强度削弱 它给删除归纳变量创造机会
9.1 优化的主要种类 9.1.7 强度削弱和归纳变量删除 • j和t 4的值步伐一致地变化 • 这样的变量叫做归纳变量 • 在循环中有多个归纳变量时, 也许只需要留下一个 • 这个操作由归纳变量删除 过程来完成 • 对本例可以先做强度削弱 它给删除归纳变量创造机会 j = j −1 t4 = 4 j t5 = a[t4 ] if t5 > v goto B3 B3
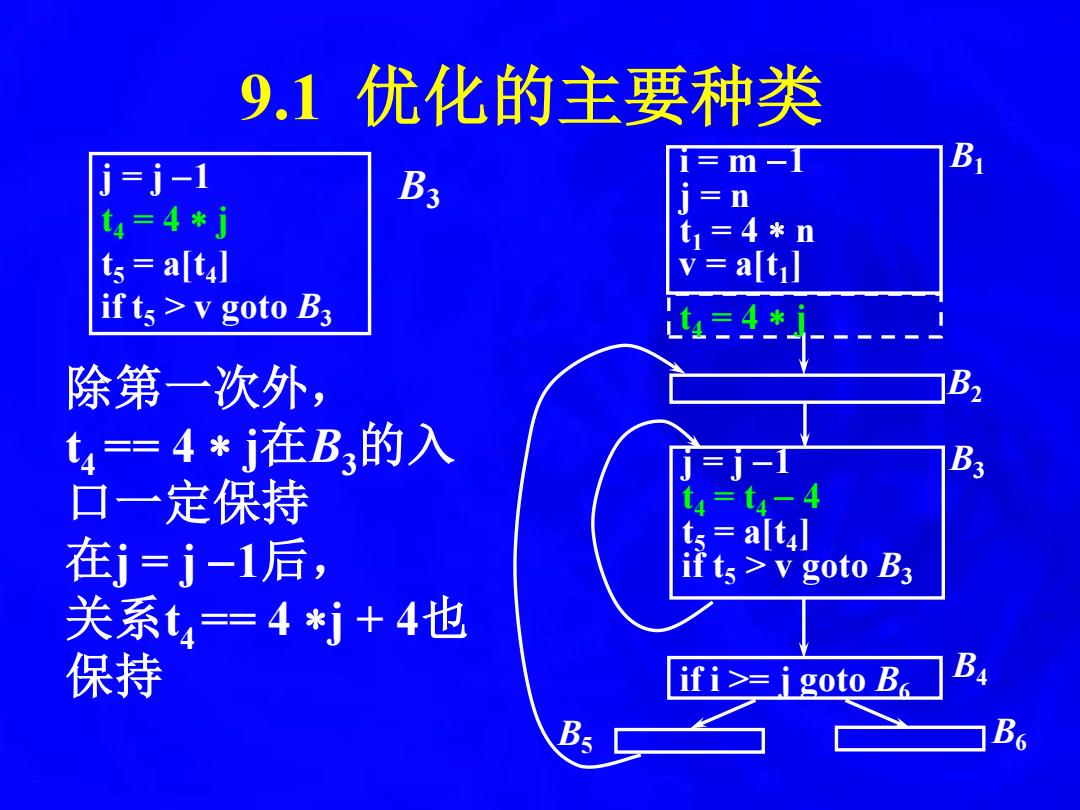
9.1优化的主要种类 =j-1 m一 B B3 n t4=4*j t 4*n ts alt] if ts v goto B3 除第一次外, t4=4*j在B3的入 j= 口一定保持 在j=j-1后, if ts v goto B3 关系t4=4*j+4也 保持 ifi>=i goto Bo B
9.1 优化的主要种类 i = m −1 j = n t1 = 4 n v = a[t1 ] B1 B2 j = j −1 t4 = t4 − 4 t5 = a[t4 ] if t5 > v goto B3 B4 B3 B5 B6 t4 = 4 j if i >= j goto B6 j = j −1 t4 = 4 j t5 = a[t4 ] if t5 > v goto B3 B3 除第一次外, t 4 == 4 j在B3的入 口一定保持 在j = j −1后, 关系t 4 == 4 j + 4也 保持
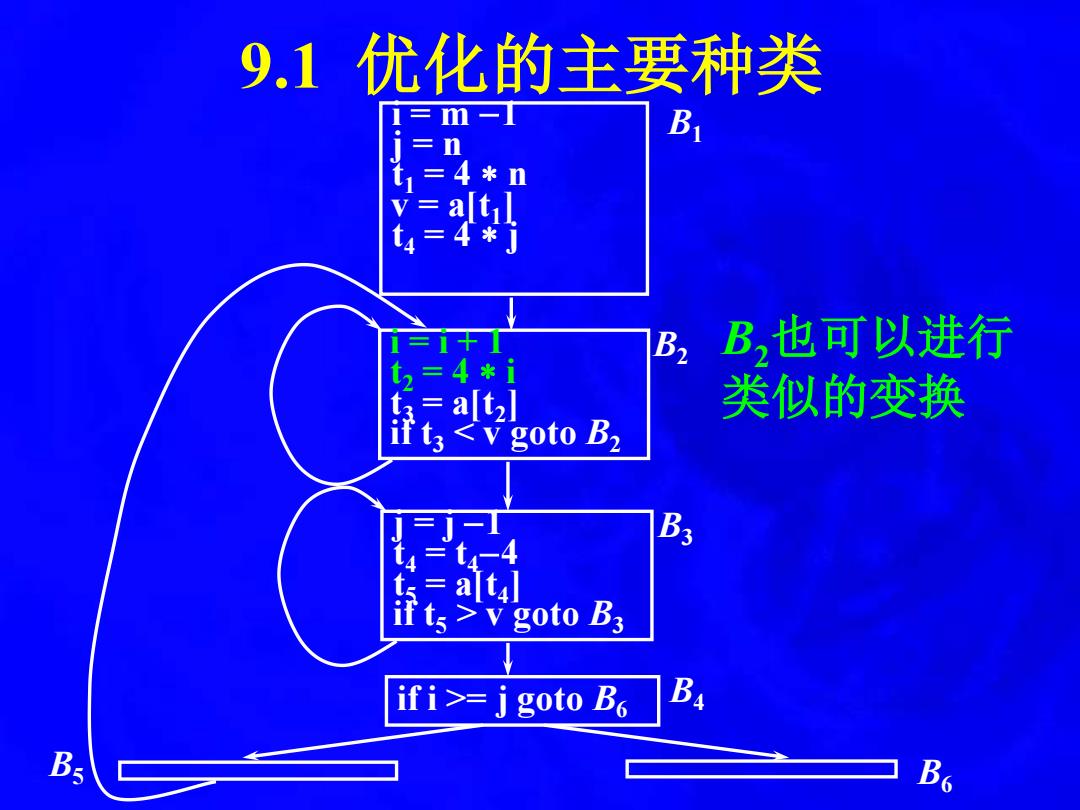
9.1优化的主要种类 三m一 B n =4*n 4*了 B2 B,也可以进行 4*i a[t 类似的变换 goto B2 ifts>v goto B3 ifi>=j goto B B B
9.1 优化的主要种类 i = m −1 j = n t1 = 4 n v = a[t1 ] t4 = 4 j i = i + 1 t2 = 4 i t3 = a[t2 ] if t3 < v goto B2 B1 B2 j = j −1 t4 = t4−4 t5 = a[t4 ] if t5 > v goto B3 if i >= j goto B6 B4 B3 B5 B6 B2也可以进行 类似的变换
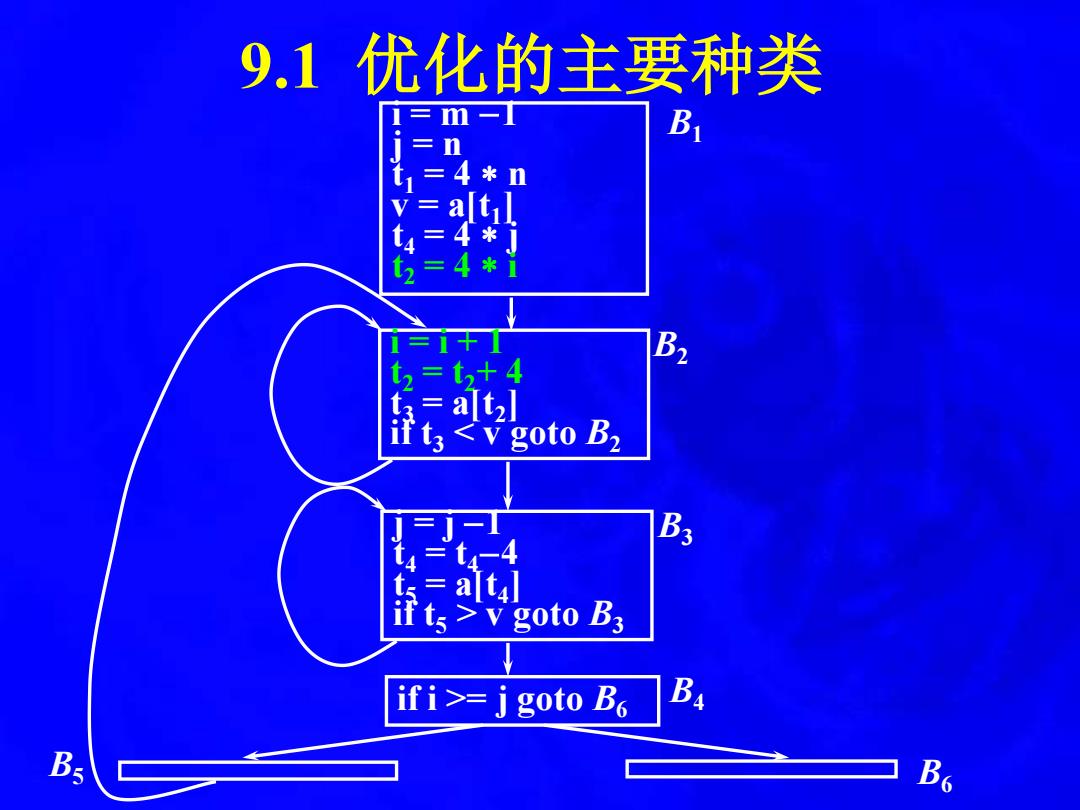
9.1优化的主要种类 1三m一 B n 4 *n a 4 B2 alt <V goto B2 B: 三 if ts v goto B3 ifi>=j goto B B
9.1 优化的主要种类 i = m −1 j = n t1 = 4 n v = a[t1] t4 = 4 j t2 = 4 i i = i + 1 t2 = t2+ 4 t3 = a[t2] if t 3 < v goto B 2 B 1 B 2 j = j − 1 t 4 = t 4 − 4 t 5 = a[t 4 ] if t 5 > v goto B 3 if i >= j goto B 6 B 4 B 3 B 5 B 6
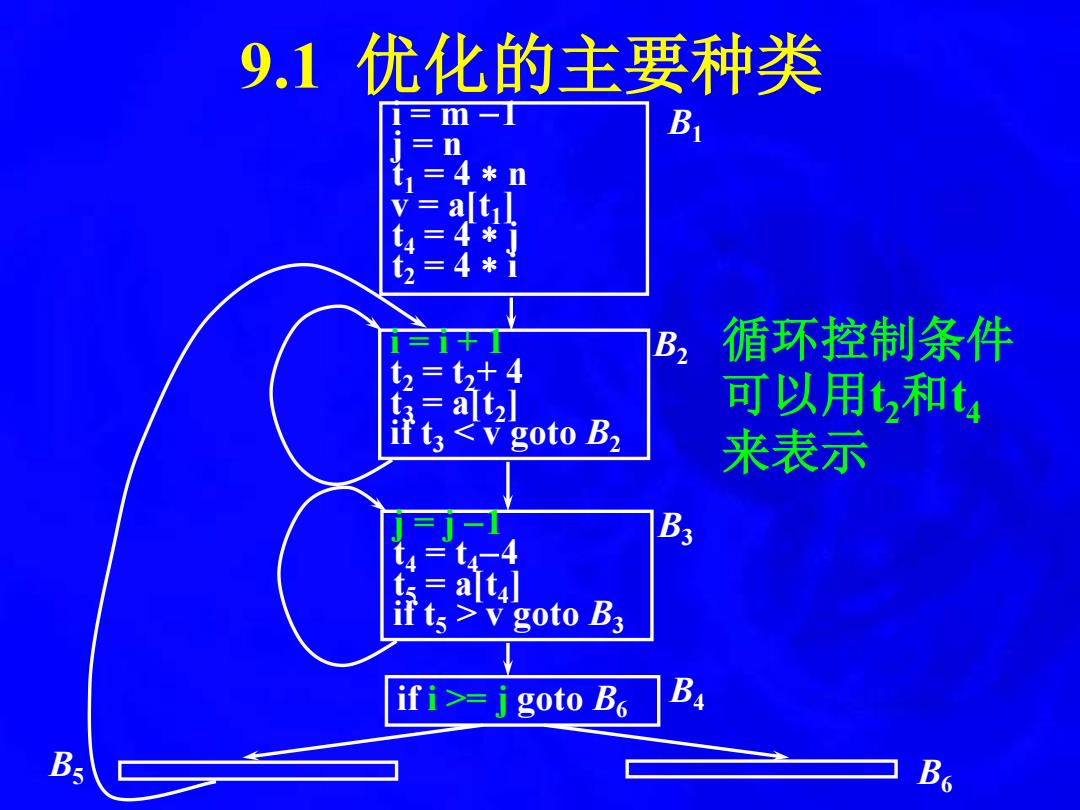
9.1优化的主要种类 m B n a 4 B2 循环控制条件 t3+ alt 可以用,和t <V goto B2 来表示 4 if ts v goto B3 ifi>=j goto B B
9.1 优化的主要种类 i = m −1 j = n t1 = 4 n v = a[t1] t4 = 4 j t2 = 4 i i = i + 1 t2 = t2+ 4 t3 = a[t2] if t 3 < v goto B 2 B 1 B 2 j = j − 1 t 4 = t 4 − 4 t 5 = a[t 4 ] if t 5 > v goto B 3 if i >= j goto B 6 B 4 B 3 B 5 B 6 循环控制条件 可以用 t 2 和 t 4 来表示