
Conditional Mean and Regression Analysis Example 1:Consumption Function Let Y be consumption,X be disposable income.Then E(YX)=C(X)is called a consumption function,which signifies how consumption depends on income.The first derivative of the consumption function C(X)is called the marginal propensity to consume(MPC): MPC=C'(X)= dE(Y X) dx MPC is a very important concept in Keynes'multiplier effect analysis. Furthermore,if Y denotes food consumption,then according to Engel's law,MPC is an decreasing function of X.Therefore,one can verify Engel's law by empirically testing whether C(X)is a decreasing function of X. ADVANCED ECONOMETRICS General Regression Analysis May12,2021 21
ADVANCED ECONOMETRICS General Regression Analysis May 12, 2021 21 Example 1: Consumption Function Conditional Mean and Regression Analysis

Conditional Mean and Regression Analysis Example 2:Production Function Let Y be output,X be labor,capital and raw materials.Then the regres- sion function E(YX)=F(X)is called a production function,which tells too much output can be produced given the amount of inputs X. Most well-known examples of production functions are the Cobb-Dauglas and translog functions (see,xxx).A production function can be used to test the constant return to scale (CRS)hypothesis.CRS is defined as follows: λF(X)=F(AX)for all入>0. ADVANCED ECONOMETRICS General Regression Analysis May12,2021 22
ADVANCED ECONOMETRICS General Regression Analysis May 12, 2021 22 Example 2: Production Function Conditional Mean and Regression Analysis

Conditional Mean and Regression Analysis Example 3:Cost Function Let Y be the production cost to produce output X.Then the regression function E(YX)=C(X)is called a cost function.For a monopolistic firm or industry,its marginal cost is a decreasing function of output X, namely, dE(Y X) C(X)>0, dX d2E(Y X) dX2 =C"(X)<0. This property implies that the cost function for a monopolistic firm is a nonlinear function of output X. ADVANCED ECONOMETRICS General Regression Analysis May12,2021 23
ADVANCED ECONOMETRICS General Regression Analysis May 12, 2021 23 Example 3: Cost Function Conditional Mean and Regression Analysis
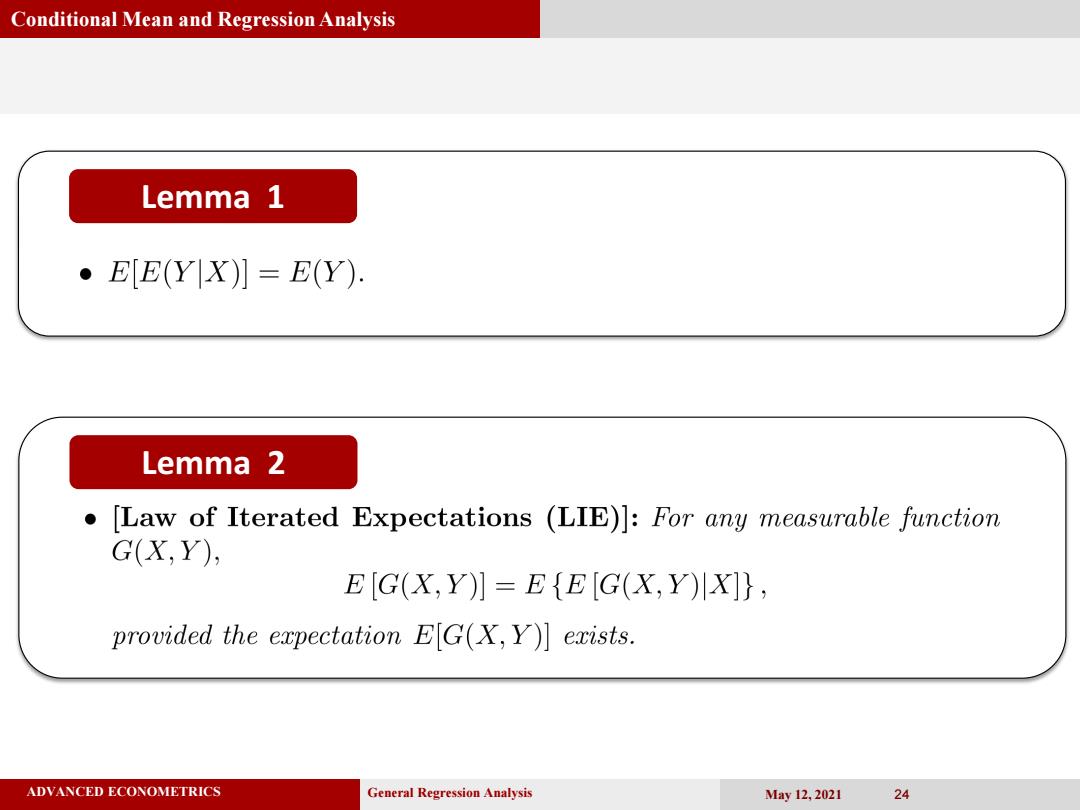
Conditional Mean and Regression Analysis Lemma 1 ●E[E(YX)]=E(Y): Lemma 2 ● [Law of Iterated Expectations (LIE)]:For any measurable function G(X,Y), E[G(X,Y)】=E{E[G(X,Y)川X]}, provided the expectation EG(X,Y]exists. ADVANCED ECONOMETRICS General Regression Analysis May12,2021 24
ADVANCED ECONOMETRICS General Regression Analysis May 12, 2021 24 Conditional Mean and Regression Analysis Lemma1 Lemma 1 Lemma 2 Lemma 2

Conditional Mean and Regression Analysis ·Proof: We consider the case of the joint continuous distribution of (Y,X)'only. By the multiplication rule that the joint pdf f(x,y)=fyx(y)fx(x), we have EtG(x,r)- G(x,y)fxv(x,y)dxdy = G(x,y)fyx(ylx)fx(x)dxdy G(,)fvlix (ulerydiy fx(eyts E[G(X,Y)Xx]fx(x)da =EE G(X,Y X To be continued ADVANCED ECONOMETRICS General Regression Analysis May12,2021 25
ADVANCED ECONOMETRICS General Regression Analysis May 12, 2021 25 Proof: Proof: Conditional Mean and Regression Analysis To be continued