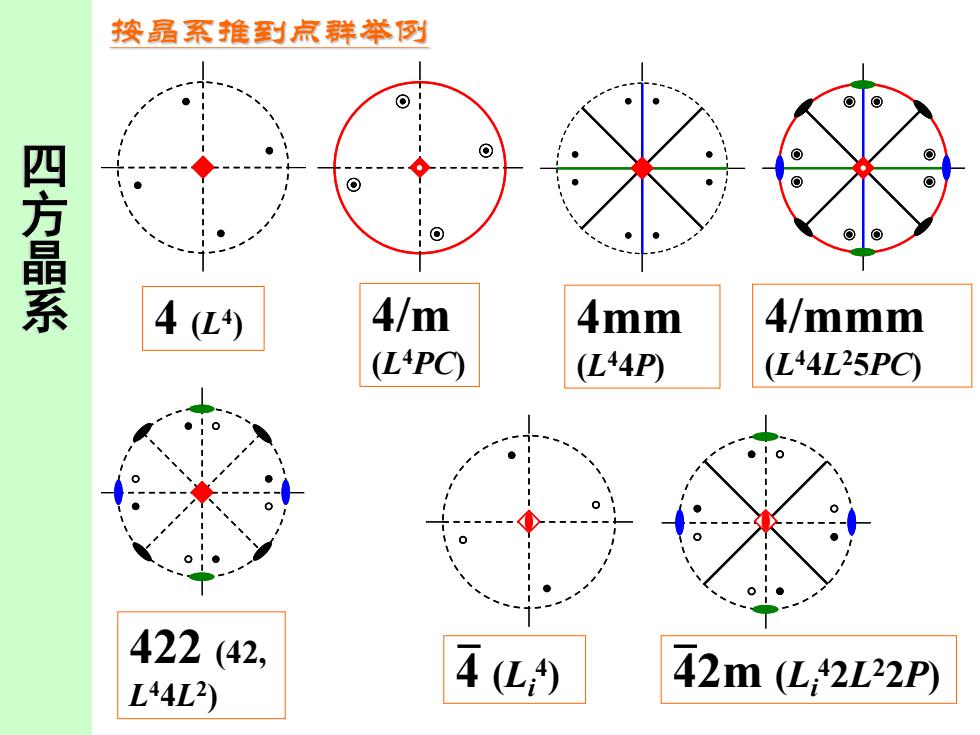
按晶系推到点群举例 四方晶系 4(L) 4/m 4mm 4/mmm (LPC) (L44P) (L44L25PC) 422(42, L44L2) 4(L) 42m(L42L22P)
四 方 晶 系 4 (L4 ) 4/m (L4PC) 4mm (L44P) 4/mmm (L44L25PC) 422 (42, L44L2 ) 4 (Li 4 ) 42m (Li 42L22P) 按晶系推到点群举例
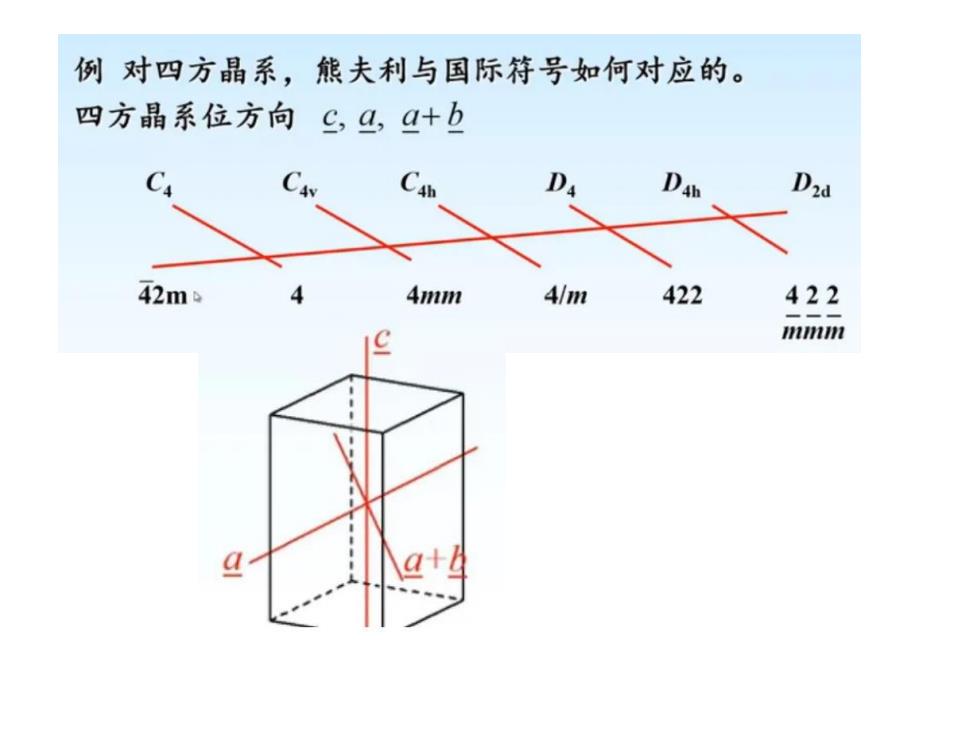
例对四方晶系,熊夫利与国际符号如何对应的。 四方晶系位方向C,4,4+b D2d 42m 4mm 4/m 422 422 11111m

从旋转点群推导32种点群点群的熊夫利斯持号 11种纯旋转群: 2 34 6 222 32 422 622 23432 C1 C2 C3 C4 C6 D2 D3 Da T 循环点群 二面体点群 丘方点群 11种中心对称,点群: 12Im341m61m mmm 3m 4/mmm 6/mmm m3 m3m S2 C2h S6 C4h Ceh D2h D3d Dih 06h Th "◆10种新子群: 12m 34m 6/m mmm 3m 4/mmm 6/mmm m3 m3m m 4 6 mm2 3m 4mm 42m 6mm 62m 43m Cih S4 C3h C2v C3v C4v D2d Cev D3h d
从旋转点群推导32种点群 点群的熊夫利斯符号 11种纯旋转群: 1 2 3 4 6 222 32 422 622 23 432 C1 C2 C3 C4 C6 D2 D3 D4 D6 T O 循环点群 二面体点群 立方点群 11种中心对称点群: m3 m3m S2 C2h S6 C4h C6h D2h D3d D4h D6h Th Oh 1 2/m 3 4/m 6/m mmm 3m 4/mmm 6/mmm 10种新子群: 1 2/m 3 4/m 6/m mmm 3m 4/mmm 6/mmm m3 m3m C1h S4 C3h C2v C3v C4v D2d C6v D3h Td m 4 6 mm2 3m 4mm 42m 6mm 62m 43m

推导32种点群的熊夫利斯方案熊夫利斯挤号 五种循环群C.(5种) 123 4 6 Ch=C.×{E,o}(5种) m2/m641m6/m Cw=CnX{Eo,}(4种,C1v=Ch) mm2 3m 4mm 6mm D.=Cn×{E,C2[100]}(4种) 22232 422 622 Dh=Ch×{E,oa}(4种) mmm 62m 4/mmm 6/mmm 非真旋转S。(3种,n=2,4,6) 不43 Dad=S2m×{E,C2[100]}n=2,3共2种) 3m 42m 立方点群(无主轴)5种: 23 m3 43m432 m3m T,Th>Tde O,On
推导32种点群的熊夫利斯方案 熊夫利斯符号 五种循环群 Cn (5 种) Cnh = Cn×{E, σh } (5 种) Cnv = Cn×{E, σv } (4 种, C1v=C1h) 非真旋转 Sn (3 种,n =2, 4, 6) Dn = Cn×{E, C2 [100] } (4 种) Dnh = Cnh×{E, d } (4 种) Dnd = S2n × {E, C2 [100] } (n =2, 3 共2种) 立方点群(无主轴)5 种: T, Th , Td , O, Oh 1 2 3 4 6 m 2/m 6 4/m 6/m mm2 3m 4mm 6mm 222 32 422 622 mmm 62m 4/mmm 6/mmm 1 4 3 3m 42m 23 m3 43m 432 m3m