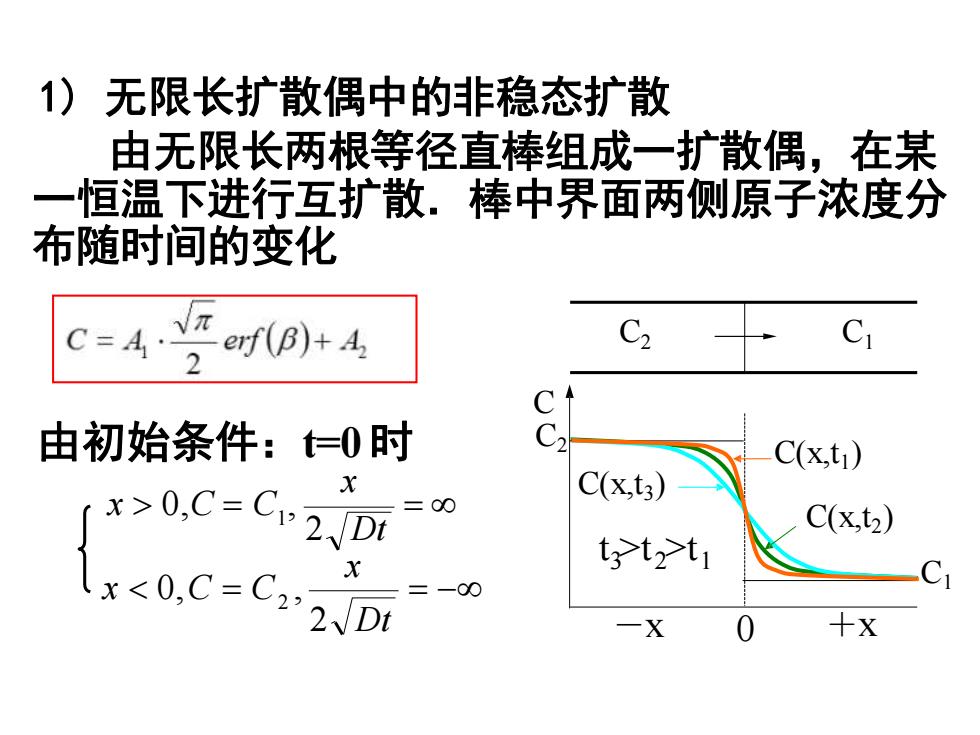
)无限长扩散偶中的非稳态扩散 由无限长两根等径直棒组成一扩散偶,在某 一恒温下进行互扩散.棒中界面两侧原子浓度分 布随时间的变化 C) C2 C 由初始条件:仁0时 C(x,t) 1x>0,C=C2D C(x,t3) =00 C(x,t2) x<0,C=C22、D t tt =一00 -X +X
C2 C1 C1 C C2 C(x,t1 ) C(x,t2 ) C(x,t3 ) t >t >t 3 2 1 -x 0 +x 由初始条件:t=0时 x x 0,C = C1 , = = − 2 Dt x 2 Dt x 0,C = C , 2 1) 无限长扩散偶中的非稳态扩散 由无限长两根等径直棒组成一扩散偶,在某 一恒温下进行互扩散.棒中界面两侧原子浓度分 布随时间的变化 SCHOOL OF MATERIALS SCIENCE AND ENGINEERING OF XI`AN JIAOTONG UNIVERSITY

代入通解得 CI=A1+A2 C2=-A1+A2 A1=- C2-C1 则, 2 (A2=C +Cl 2 故特解为: 2 THE END
则, A1 = − C2 −C1 2 A2 = C2 +C1 2 故特解为: C = − 2 2 C2 + C1 C2 − C1 代入通解得 C1=A1+A2 C2=-A1+A2 THE END SCHOOL OF MATERIALS SCIENCE AND ENGINEERING OF XI`AN JIAOTONG UNIVERSITY erf 𝑋 2 Dt × 2 Π
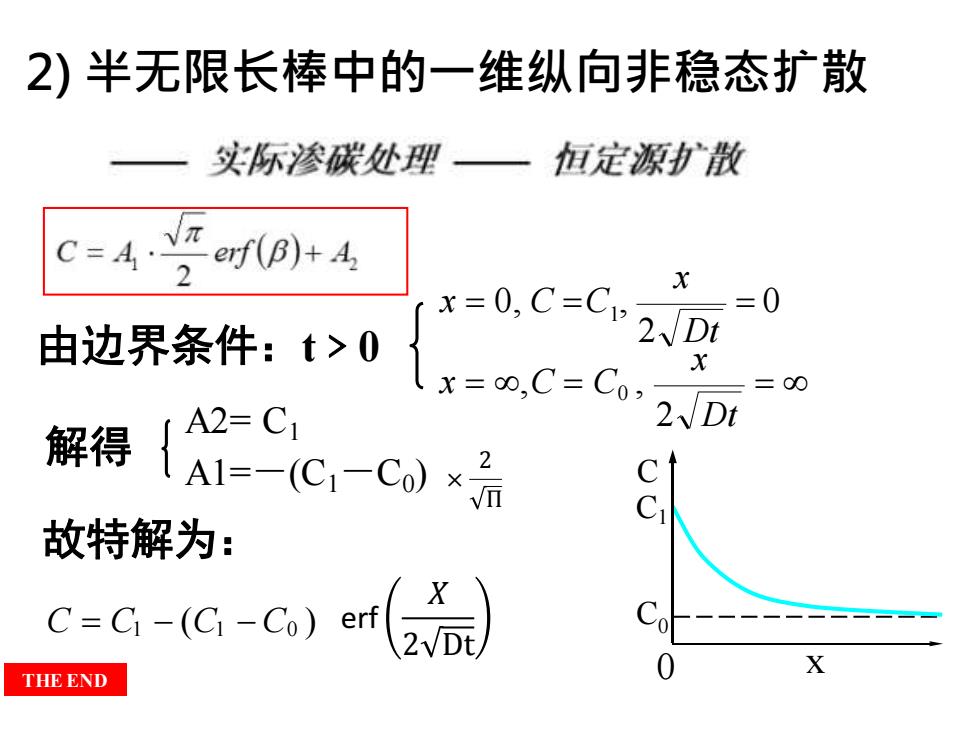
2)半无限长棒中的一维纵向非稳态扩散 实际渗碳处理一 恒定源散 C4) x=0,C=C, =0 由边界条件:t>0{ x=o0,C=C0, =00 解得 A2=C A1=-C,-C)x 故特解为: C=CI-(Ci-Co)erf Co X THE END
C C1 0 x C0 1 = 0 2 Dt x x = 0, C =C , = x 2 Dt x = ,C = C0 , 解得 故特解为: C = C1 − (C1 −C0 ) 由边界条件:t﹥0 2) 半无限长棒中的一维纵向非稳态扩散 A2= C1 A1=-(C1-C0 ) THE END SCHOOL OF MATERIALS SCIENCE AND ENGINEERING OF XI`AN JIAOTONG UNIVERSITY erf 𝑋 2 Dt × 2 Π

例题120钢齿轮927℃气体渗碳,控制炉内渗 碳气氛使工件表面碳含量wc=1.0%,假定碳在 该温度时的扩散系数D=1.28×10-m2:s-1.如果 将工件中碳含量wc=0.4%处至表面的距离定义 为渗碳层深度,试计算: 1) 渗碳詹深度送0.5mm所需的渗碳时间 2)渗碳层深度达1mm所需的渗碳时间 解1)C=G-(G-C)erf 2√D元 1.0-0.4 C=0.4%C1=1.0%C0=0.2% 1.0-0.2 =0.75 由误差函数表,并用内差法求得 —≈0.8138 2Dt 则, t= ≈7373s 4D×0.81382 THE END
例题1 20钢齿轮927℃气体渗碳,控制炉内渗 .如果 碳气氛使工件表面碳含量 wC =1.0% ,假定碳在 该温度时的扩散系数 D=1.28×10-11m2·s-1 将工件中碳含量 wC = 0.4%处至表面的距离定义 为渗碳层深度,试计算: 1) 渗碳层深度达0.5mm 所需的渗碳时间 2) 渗碳层深度达1mm 所需的渗碳时间 解 1) C = C1 − (C1 − C0 ) C=0.4% C1=1.0% C0=0.2% 由误差函数表,并用内差法求得 x 0.8138 2 Dt 则, x 2 t = 7373s 4D 0.81382 THE END SCHOOL OF MATERIALS SCIENCE AND ENGINEERING OF XI`AN JIAOTONG UNIVERSITY erf 𝑋 2 Dt erf 𝑋 2 Dt = 1.0 − 0.4 1.0 − 0.2 = 0.75在此处键入公式

>对渗碳问题:已知钢材含碳量C。、渗碳气体碳势C, 要求渗碳浓度C*一定时, C-C=常数 Cg-C。 故6=a√Dt,若D一定,则6xd THE END
THE END SCHOOL OF MATERIALS SCIENCE AND ENGINEERING OF XI`AN JIAOTONG UNIVERSITY