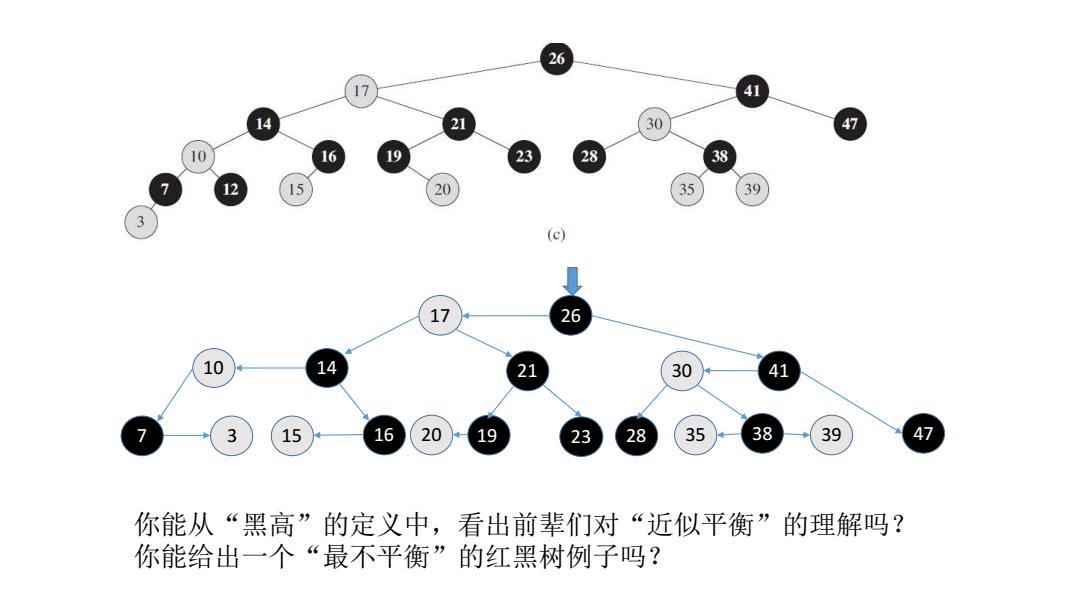
26 41 21 30 47 19 23 38 20 35 39 (c) 17 26 10 14 21 30 41 3 15 16 20 28 35 38 39 47 你能从“黑高”的定义中,看出前辈们对“近似平衡”的理解吗? 你能给出一个“最不平衡”的红黑树例子吗?
26 41 17 14 7 16 38 47 21 19 23 28 30 15 10 3 20 35 39 你能从“黑高”的定义中,看出前辈们对“近似平衡”的理解吗? 你能给出一个“最不平衡”的红黑树例子吗?
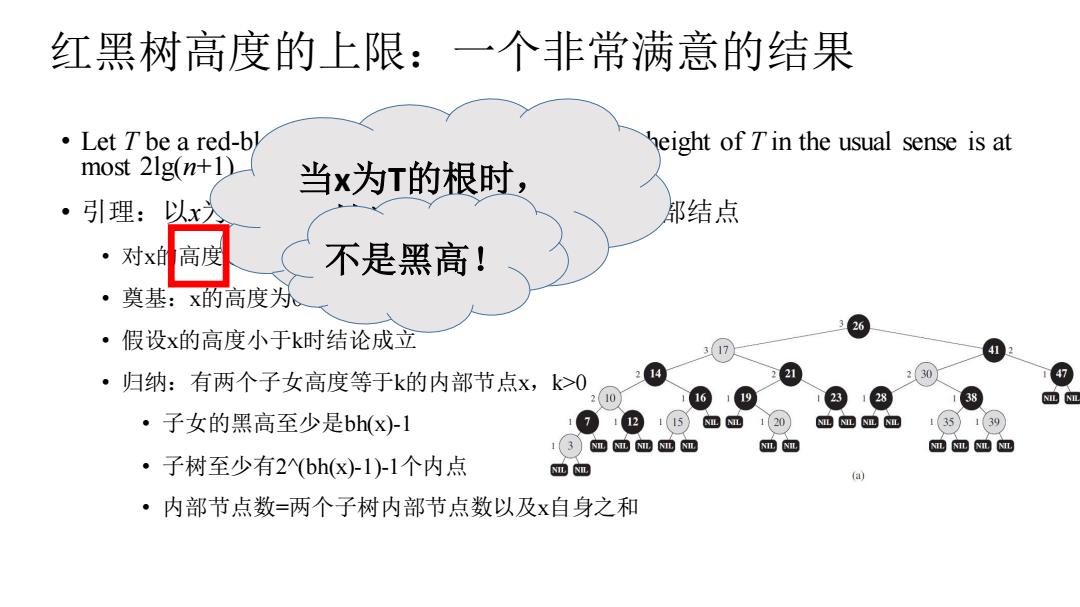
红黑树高度的上限:一个非常满意的结果 ·Let Tbe a red-bh height of Tin the usual sense is at most 21g(n+1) 当x为T的根时, ·引理:以x 邰结点 ·对x日 高度 不是黑高! ·奠基:x的高度为 ·假设x的高度小于k时结论成立 17 ·归纳:有两个子女高度等于k的内部节点x,k>0 230 47 2(10 119 128 NIL NIL ·子女的黑高至少是bh(x)-1 1(15m120 NIL NILNIL NID 1(35)1(39 m AI N10 NIL NR ·子树至少有2(bh(x)-1)1个内点 NINI (a) ·内部节点数=两个子树内部节点数以及x自身之和
红黑树高度的上限:一个非常满意的结果 • Let T be a red-black tree with n internal nodes,the height of T in the usual sense is at most 2lg(n+1). • 引理:以x为根的红黑树子树至少包含2 bh(x) -1个内部结点 • 对x的高度进行归纳 • 奠基:x的高度为0时:x是Nil,正确 • 假设x的高度小于k时结论成立 • 归纳:有两个子女高度等于k的内部节点x,k>0 • 子女的黑高至少是bh(x)-1 • 子树至少有2^(bh(x)-1)-1个内点 • 内部节点数=两个子树内部节点数以及x自身之和 当x为T的根时, 情况如何? 不是黑高!

当x就是树的根T时: ·树的内部节点数n>=2bh(T)-1 。与此同时: bh(T)和T的高h是什么关系? ·h<=2bh(T) ·n>=2bhT)-1>=2h/2-1 问题: h<=2Ig(n+1):这个结论有 什么意义?
当x就是树的根T时: • 树的内部节点数 n>=2bh(T) -1 • 与此同时: • h<=2bh(T) • n>= 2bh(T) -1>= 2h/2 -1 bh(T)和T的高h是什么关系?

问题: 一棵二叉搜索树,如果平衡性不够 好,我们是否能够改善这个平衡性? 有什么办法?为什么可以这样做?
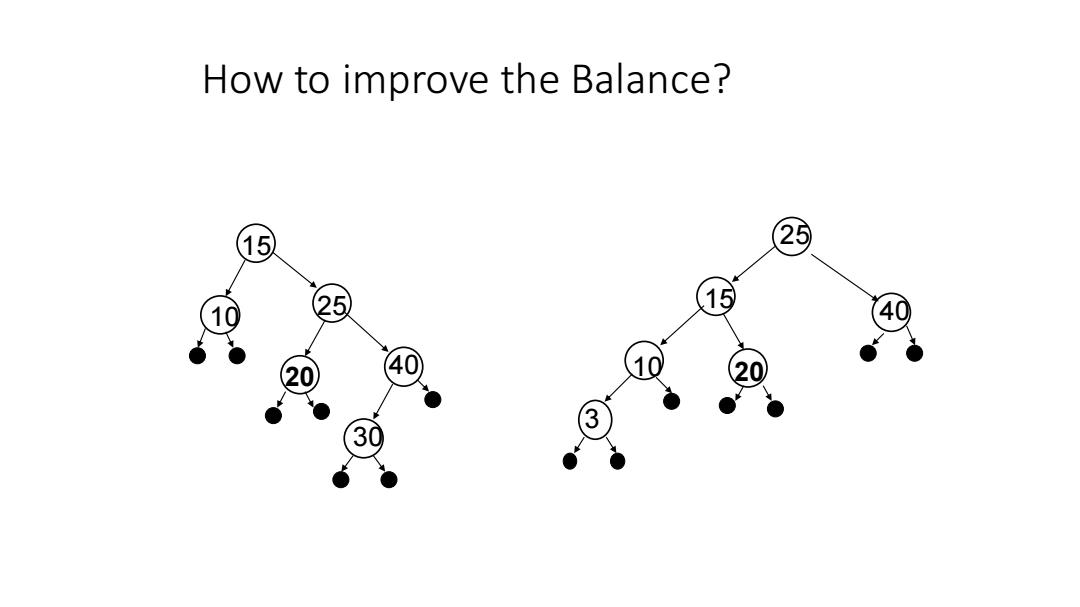
How to improve the Balance? 15 25 25 15 40 3
How to improve the Balance? 15 10 25 20 30 40 25 40 15 10 20 3