中国科学技术大学：《数据结构及其算法》课程教学资源（课件讲稿）第7章 图

数据结构 图 第七章图 主讲：张昱 重点：图在邻接矩阵和邻接表上的遍历算法 yuzhang@ustc.edu (DFS,BFS)及其应用 0551-3603804 难点：求图的最小生成树、最短路径、拓扑排 序、关键路径等算法及其应用、性能分析 1/106 2/106 第七章图 上7.1图的定义和术语(1) 7.1图的定义和术语 ■图的定义 7.2图的存储结构 ,图是由项点集合(vertex)及顶点之间的关系集 佥组成的一种数据结构。 7.3图的遗历 记为G=(口，{E)顶点集，E关系的集合 7.4图的连通性问题 ,顶点之间的关系是多对多的(m:) 7.5有向无环图及其应用 ,顶点之间的关系是否有方向性： 有向图、无向图 7.6最短路径 3/106 4/106 图 7.1图的定义和术语(2) 17.1图的定义和术语(2) ,无向图 ,有向图 ,边(，w)€E(g,wE),与w互为接点，边(%w座 ,顶点v的入度是以￥为薰头的孤的数国，记为D(归 胜于顶点和w,减者说边(w)和顶点以，相关联。 v的出度是以v为薰尾的蕴的数司，记为OD(吵防 ,顶点v的度是和相关联的边的数目，记为TD(), v的度是TD()=D()+OD(. 。有向图 ■路径与连通性 ,弧<，w>∈E(,w∈，w为燕头为蕴L:顶燕v绝 路径、简单路径、回路环)、简单回路 接到顶越w,顶燕w邻接自顶点，孤<以w>和顶项点 ,相关联。 顶，点之门的连通性、无向连通困、有向强连通困 5/106 图 6/106 图

1/106 数据结构——图 主讲：张昱 yuzhang@ustc.edu 0551-3603804 2/106 重点：图在邻接矩阵和邻接表上的遍历算法 (DFS, BFS)及其应用 难点：求图的最小生成树、最短路径、拓扑排 序、关键路径等算法及其应用、性能分析 第七章 图 3/106 第七章 图 7.1 图的定义和术语 7.2 图的存储结构 7.3 图的遍历 7.4 图的连通性问题 7.5 有向无环图及其应用 7.6 最短路径 4/106 7.1 图的定义和术语(1) „ 图的定义 „ 图是由顶点集合(vertex)及顶点之间的关系集 合组成的一种数据结构。 记为G = (V, {E}) V-顶点集，E-关系的集合 „ 顶点之间的关系是多对多的(m : n) „ 顶点之间的关系是否有方向性： 有向图、无向图 5/106 7.1 图的定义和术语(2) „ 无向图 „ 边(v,w) ∊ E (v,w ∊V)，v与w互为邻接点，边( v, w )依 附于顶点v和w，或者说边( v, w )和顶点v, w相关联。 „ 顶点v 的度是和v相关联的边的数目,记为TD(v) 。 „ 有向图 „ 弧<v,w> ∊ E (v,w ∊V)，w为弧头, v为弧尾; 顶点v 邻 接到顶点w，顶点w 邻接自顶点v，弧< v, w >和顶点 v、w相关联。 6/106 7.1 图的定义和术语(2) „ 有向图 „ 顶点v 的入度是以v 为弧头的弧的数目,记为ID(v); v 的出度是以v为弧尾的弧的数目,记为OD(v); v 的度是TD(v) = ID(v) + OD(v)。 „ 路径与连通性 路径、简单路径、回路(环)、简单回路 顶点之间的连通性、无向连通图、有向强连通图

7.1图的定义和术语(3) 7.1图的定义和术语(4) ,对于有向图G ,对于无向图G ,VVV:VV,是从V,到V,的路径，不是简单路径； ,V VVV.V2是V,和V,间的路径，但不是简单路径； ,VV,是简单路径： ,VV,是简单路径； ▣VV,V:VV3VV是环，不是简单环； G ,V2VVV2VV,V是环，但不是简单环 ·VVV,V是简单环. V2VgVV是简单环。 .ID(V)-1.OD(V)-2,TD(V)-3 ■TDV,-2 ·Y柔V是连通的：从V,到，是连通的，⑦ ⊙ ,V和V,是连通的 但从V到V,是不连通的. ,G,是连通图 ,G不是强连通图 71106 回 8/106 图 7.1图的定义和术语(5) 7.1图的定义和术语(6) ·子图、连通性 ·对于G=(V,{E),它的子图 G ·子图、连通性 G满足： B ·生成树极小连通子图 A 1)V'S V; ,极大、极小是就边数的多少 ©⑩E 2)E'S E: @ 而言的 3)G'-(V”,{E9) o@① ,连通分量极大连通子图 ①①® ①①⑧ ,强连通分量一有向国中的板心 大强连通子图 连通分量 生成树 9/106 图 10/106 图 71图的定义和术酒(7) 71图的定义和术语（8) ■边/弧数目 ·边/弧数目 用n表示图中顶点数目，用e表示田中边戒孤的数目 思考：若无向图中有21条边，则： 。无向国：0≤e≤h(m-1) 1)保特斌图不连通至少应具有多少个顶点？ 完全因e=以(m-l) 2)保特斌图连通玉少有多少个项点，玉多有多少个项 ,有向因：0≤e≤m-) 有向完全图e=n(n-I) 点？ ,希城困：e<nlogn 1)m个顶点形成完全困，另一个顶燕与这m个顶点不 斜密因 连 。若困中边或孤上有权，则该困称为网 ⅓m(m-1)-21m-7之-mt1-8 2)至少有7个顶点（完全困），至多有22个顶点（生成树） 有向因、有向网、无向园、无向网 图 12/106

7/106 7.1 图的定义和术语(3) „ 对于有向图G1 „ V1V3V4V1V2 是从V1 到V2 的路径, 不是简单路径； „ V1V2是简单路径; „ V1V3V4V1V3V4V1是环,不是简单环; „ V1V3V4V1是简单环。 „ ID(V1)=1, OD(V1)=2, TD(V1)=3 „ V1和V4是连通的；从V1到V2是连通的， 但从V2到V1是不连通的。 „ G1不是强连通图 V1 V3 V2 V4 G1 8/106 7.1 图的定义和术语(4) „ 对于无向图G2 „ V1V2V3V5V2 是V1和V2间的路径，但不是简单路径； „ V1V2是简单路径； „ V2V3V5V2V3V5V2是环，但不是简单环 „ V2V3V5V2是简单环。 „ TD(V1)=2 „ V1和V4是连通的 „ G2是连通图 V1 V2 V3 V4 V5 G2 9/106 7.1 图的定义和术语(5) „ 子图、连通性 „ 对于G=(V, {E})，它的子图 G'满足： 1) V'⊆ V; 2) E'⊆ E; 3) G'=(V', {E'}) „ 连通分量—极大连通子图 „ 强连通分量—有向图中的极 大强连通子图 G3 D E I G H K A C B F L J M A C B F L J M I G H K 连通分量 10/106 7.1 图的定义和术语(6) „ 子图、连通性 „ 生成树—极小连通子图 „ 极大、极小是就边数的多少 而言的 G3 D E I G H K A C B F L J M A C B F L J M I G H K 生成树 11/106 7.1 图的定义和术语(7) „ 边/弧数目 用n 表示图中顶点数目，用e 表示图中边或弧的数目 „ 无向图：0 ≤ e ≤ ½ n(n-1) 完全图 e = ½ n(n-1) „ 有向图：0 ≤ e ≤ n(n-1) 有向完全图 e = n(n-1) „ 稀疏图： e < nlogn 稠密图 „ 若图中边或弧上有权，则该图称为网 有向图、有向网、无向图、无向网 12/106 7.1 图的定义和术语(8) „ 边/弧数目 思考：若无向图中有21条边，则： 1) 保持该图不连通至少应具有多少个顶点？ 2) 保持该图连通至少有多少个顶点，至多有多少个顶 点？ 1) m个顶点形成完全图，另一个顶点与这m个顶点不 连通 ½ m(m-1)=21 Î m=7 Î n=m+1=8 2) 至少有 7 个顶点(完全图)，至多有22个顶点(生成树)

敌据关系R:: 17.1图的定义-ADT Graph R=IVRI R=w水weV且P,w,w表示从v到w的到，谓词 P(vw) 定义了弧w的意义或信息制 ■ADT Graph 基本操作，。 ,查找：LocateVex(G,u) G”物米的项点集课是国中的集合 GetVex(G,v) 操作结果，按V和VR的定义构造图G FirstAdjVex(G,v) DestroyGrapl(&G) NextAdjVex(G,v,w) 初始杀件：图G存在 ■插入：InsertVex(&G,v) 操作结果：销毁图G LocateVex(G n) InsertArc(&G,v,w) 初始杀件：图G已存在，a和G中项点有相同特征 ,副除：DeleteVex(&G,v) 操作结果：若G中存在项点山，返回该项点在图中位置。否则返 DeleteArc(&G,v,w) 回其它信 ,通历：DFSTraverse(G,v,Visit() GetVex(G v) 初始条件：图G存在，v是G中某个顶点 BFSTraverse(G,v,Visit()) 回 作结来：返回v的值 13/106 14/106 图 PutVex(&G v,value) 初始条件：图G存在，v是G中某个顶点 InsertAre&G.v.w) 初始条件：图G存在，v和W是G中两个页点 操作结果：对v赋值vae 操作结果：在图G中增添到w>,若G是无向的，则还应增添对 初始条件：图G存在，v是G中某个顶点 称w,v DeleteArc(&G.v.w) 操作结果：返回v的第一个邻接项点。若顶点在G中设有邻接项点， 初始条件：图G存在，v和w是G中两个页点 则返回“空” 操作结果：别除G中的买w,若G是无向的，则还应副除对称 NextAdiVex(G vw 初暗亲作，图G存在，v是G中某个项点，w是v的邻接顶点 DESTraverse(G v,visit 操作结果：返回v的（相对于w的下一个邻接顶点。若w是v的最 初始件：图G存在，v是G中某个顶点，s城是对面点的应用函 后一个邻接点，则返回“空”。 数 InsertVex(&G v) 作结果：从点起深度优先滴历图G,并对每个点调用函裁 初始条件：图G存在，v和G中顶点有相同特征 it一次且至多一次。一且i()失败，刚操作失收 操作结果，在图中增添新项点 BFSTraverse(G v,visit( 初黯条件：图G存在，v是G中某个顶点，是对面点的应用函 DeleteVex(&G v) 初始条件：图G存在，v是G中某个顶点 搡作结果：从顾点v起广度优先遍历图G,并对每个顶点调用函数 操作结果：删除G中顶点￥及其相关的弧 it)一次且至多一次.一旦i此)失敞，操作失收 圆 ADT Graph 15/106 16/106 图 7.2图的存储结构(1) 生72图的存储结构(2) 。图的存储表示分析 ■图的存储表示分析 。特点：顶点之间的关系是多对多(m:) ,”m和n都是不定的，无法进行非战性结构的战性化 ,顶点集的存储 “,图中的关系不能通过顺序映像（即通过顶点之间的存 用顺序表存储，不是顺序映像！ 储位置反映顶点之间的辽辉关系)反映；必须另外引入 。关系集的存储 存储空间反映顶点之间的怀接关系。 邻接矩阵、邻接表、多重邻接表、十字链表 。图的存储信息 顶燕信惠、边/孤信息 燮体信息：顶点数、边/蕴散、图的种类（有向图/有向 网/无向因/无向网) 17/106 图 18/106 回

13/106 7.1 图的定义-ADT Graph „ ADT Graph „ 查找：LocateVex(G, u) GetVex(G, v) FirstAdjVex(G, v) NextAdjVex(G, v, w) „ 插入：InsertVex(&G, v) InsertArc(&G, v, w) „ 删除：DeleteVex(&G, v) DeleteArc(&G, v, w) „ 遍历：DFSTraverse(G, v, Visit()) BFSTraverse(G, v, Visit()) 14/106 15/106 16/106 17/106 7.2 图的存储结构(1) „ 图的存储表示分析 „ 特点：顶点之间的关系是多对多(m : n) ∵m 和 n 都是不定的，无法进行非线性结构的线性化 ∴图中的关系不能通过顺序映像(即通过顶点之间的存 储位置反映顶点之间的逻辑关系)反映；必须另外引入 存储空间反映顶点之间的邻接关系。 „ 图的存储信息 顶点信息、边/弧信息 整体信息：顶点数、边/弧数、图的种类(有向图/有向 网/无向图/无向网) 18/106 7.2 图的存储结构(2) „ 图的存储表示分析 „ 顶点集的存储 用顺序表存储，不是顺序映像！ „ 关系集的存储 邻接矩阵、邻接表、多重邻接表、十字链表

17.2图的存储结构-邻接矩阵 7.2图的存储结构-邻接矩阵 ■数组表示法—邻接矩阵 ■数组表示法 邻接矩阵 #define INFINITY INT MAX typedef structf typedef enum(DG,DN,AG.AN)GraphKind: typedef struct ArcCellf ∥顶点向量 ∥顶点间的关系，无权图：0-不相邻，1-相邻 VertexType vexs[MAX_VERTEX_NUM]; ∥有权图：权值，NFINITY-不相怀 ∥关系果 int adj; AdiMatrix arcs; InfoType *info:∥这航相关信息的指针 int vexnum,arcnum;∥项，点数、边/孤数 AreCell. GraphKind kind; ∥困的种类 AdjMatrix|MAX_VERTEX_NUMIIMAX_VERTEX_NUM]: }MGraph; 19/106 回 20/106 图 7.2图的存储结构-邻接矩阵 」7.2图的存储结构-邻接矩阵 ,无向图一对称矩阵 ,有向图—未必是对称矩阵 无权图：邻接矩阵中的元素为0-不邻接； 邻接矩阵中的元素为1-邻接 G VI的 11 V1的度， 01010 出度 0000 0101 0001 值为1日 0 000 元素个 00 V1的 1100 入度 2L/106 图 22/106 图 尘7.2图的存储结构邻装矩阵 尘上72图的存储结构餐装款 。有向网一未必是对称矩阵（图7.9，P162) ·邻接表 网：权值-邻接；极限值-不邻接 无向图/网：边表，表结点的个数为边数的两倍 G 有白田/网：出边表，表结点的个数为孤数 oo 5 0o 7 oo 0o typedef struct AreNode{∥表结，点 的出 09 int adjvex;:∥弧所指向的顶点的位置 0006 struct AreNode*nextarc;/∥指向下一条孤的指针 5 InfoType *info; ArcNode; 23/106 图 24/106 图

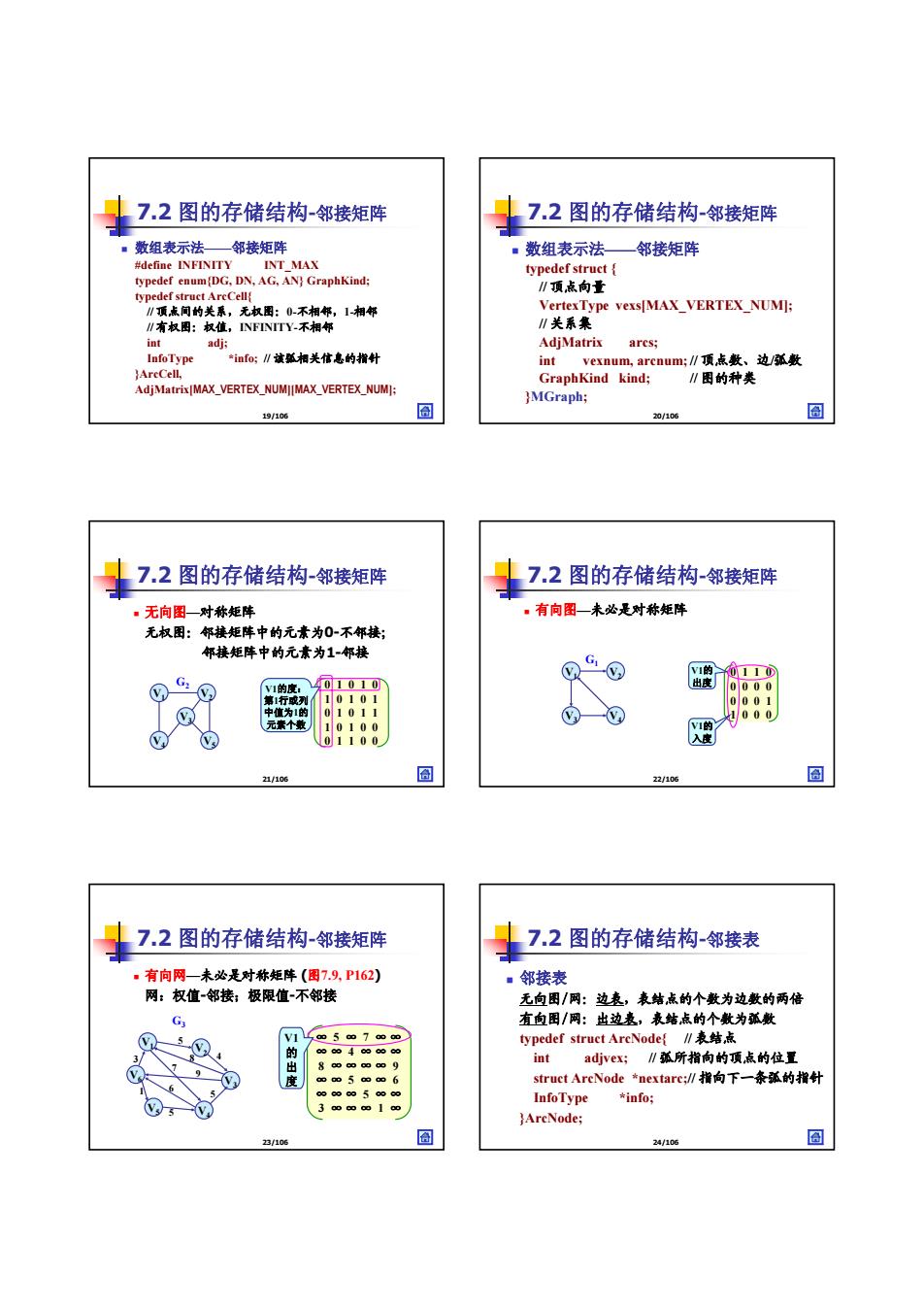
19/106 7.2 图的存储结构-邻接矩阵 „ 数组表示法——邻接矩阵 #define INFINITY INT_MAX typedef enum{DG, DN, AG, AN} GraphKind; typedef struct ArcCell{ // 顶点间的关系，无权图：0-不相邻，1-相邻 // 有权图：权值，INFINITY-不相邻 int adj; InfoType *info; // 该弧相关信息的指针 }ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; 20/106 7.2 图的存储结构-邻接矩阵 „ 数组表示法——邻接矩阵 typedef struct { // 顶点向量 VertexType vexs[MAX_VERTEX_NUM]; // 关系集 AdjMatrix arcs; int vexnum, arcnum;// 顶点数、边/弧数 GraphKind kind; // 图的种类 }MGraph; 21/106 7.2 图的存储结构-邻接矩阵 „ 无向图—对称矩阵 无权图：邻接矩阵中的元素为0-不邻接； 邻接矩阵中的元素为1-邻接 V1 V2 V3 V4 V5 G2 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0 V1的度： 第1行或列 中值为1的 元素个数 22/106 7.2 图的存储结构-邻接矩阵 „ 有向图—未必是对称矩阵 V1 V3 V2 V4 G1 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 V1的 出度 V1的 入度 23/106 7.2 图的存储结构-邻接矩阵 „ 有向网—未必是对称矩阵 (图7.9, P162) 网：权值-邻接；极限值-不邻接 V1 V2 V3 V5 V6 G3 5 8 4 3 V4 9 7 6 1 5 5 ∞ 5 ∞ 7 ∞ ∞ ∞ ∞ 4 ∞∞∞ 8 ∞∞∞∞ 9 ∞ ∞ 5 ∞ ∞ 6 ∞∞∞ 5 ∞ ∞ 3 ∞∞∞ 1 ∞ V1 的 出 度 24/106 7.2 图的存储结构-邻接表 „ 邻接表 无向图/网：边表，表结点的个数为边数的两倍 有向图/网：出边表，表结点的个数为弧数 typedef struct ArcNode{ // 表结点 int adjvex; // 弧所指向的顶点的位置 struct ArcNode *nextarc;// 指向下一条弧的指针 InfoType *info; }ArcNode;

17.2图的存储结构-邻接表 上7.2图的存储结构-邻接表 。邻接表 ·无向图/网一边表 typedef struct VNodef ∥头结点 注意：表结，点存放的是顶底在顶点顺序表中的偏号，不 VertexType data; ∥顶点信惠 是顶燕的基本信息。 ArcNode *firstare;:∥邻接表指针 V,的度 }VNode,AdjList[MAX VERTEX NUM]; o V, 3 typedef struct{ 1 V2 423 0 AdiList vertices; 2 4 31 int vexnum,arenum;∥项，点数、边/孤数 3 2 0 GraphKind kind; ∥困的种类 21 ALGraph; 25/106 回 26/106 图 7.2图的存储结构邻接表 士7.2图的存储结构-一图的创建 ,有向图/网一出边表 图的创建算法 。输入图的类型，根据类型选择相应的创建算法 0V231 。输入图的顶点数，边/弧数 IV^ V,的出度 3 ·输入并存储顶点信息 0 ·输入边/弧所关联的顶点对，将边或弧的信息存储到邻 V,的入度 师接表一出边表 接矩阵/邻接表中 , 3 教材中的算法7.1-7.3 1 0 图的存储结构不同、图的类型不同，都会形响创建算法 0 的实现细节；但是，图的总体创建流混是一致的1 2 ·邻接短阵与邻接表的对比 逆你接表一入边表 27/10 28/106 图 假设图为G,顷点数为m,边弧数为c。 邻接矩阵 邻接表 邻接垣阵 邻接表 存储空间。 0a+n2 O(nte TI(n-0(c+T2(n)-0(e'n+p2) T1m=0ate或T2a=0cn 有自图中求 入度： 图的创建算T1仙是指在输入边孤时，输入的顺点信总为项点的第号：而T2侧则指 0arc刑4第列 入度：扫描各顶点的邻接表，统计 在箱输入边孤时，输入的为顶点本身的信息，此时需要查找顶点在图中的 第顶点的入 位置： 出度 出底总Grf时第1m 表结点的ar为的表结点个数 T(n)=O(nte) 无向图中求 分cacf利[a4(第行之和或 有向时中求 入废：第i列中a值不为NFINITY 出度：Gvertices]firstare所指向 第顶点的度 总aaca第i收r Gvces.firstare所指向的邻接 第顶点的入 的元素个数， 的邻接表包含的结点个数： 表包含的结点个数。 出度 出度：第i行中a值不为NNT 无向网中求第i行例中ad值不为NFINITY的 的元素个数 第顶点的度元素个数 29106 30/106 图

25/106 7.2 图的存储结构-邻接表 „ 邻接表 typedef struct VNode{ // 头结点 VertexType data; // 顶点信息 ArcNode *firstarc;// 邻接表指针 }VNode, AdjList[MAX_VERTEX_NUM]; typedef struct { AdjList vertices; int vexnum, arcnum;// 顶点数、边/弧数 GraphKind kind; // 图的种类 }ALGraph; 26/106 7.2 图的存储结构-邻接表 „ 无向图/网—边表 注意：表结点存放的是顶点在顶点顺序表中的编号，不 是顶点的基本信息。 V1 V2 V3 V4 V5 G2 V1 V2 V3 V4 V5 0 1 2 3 4 3 1 ^ 4 2 2 0 ^ 4 3 1 ^ 0 ^ 2 1 ^ V1的度 27/106 7.2 图的存储结构-邻接表 „ 有向图/网—出边表 V1 V3 V2 V4 G1 V1 V2 ^ V3 V4 0 1 2 3 2 1 ^ 0 ^ 3 ^ 邻接表—出边表 V1 V2 V3 V4 0 1 2 3 3 ^ 0 ^ 2 ^ 0 ^ 逆邻接表—入边表 V1的出度 V1的入度 28/106 7.2 图的存储结构—图的创建 „ 图的创建算法 „ 输入图的类型，根据类型选择相应的创建算法 „ 输入图的顶点数，边/弧数 „ 输入并存储顶点信息 „ 输入边/弧所关联的顶点对，将边或弧的信息存储到邻 接矩阵/邻接表中 教材中的算法7.1~7.3 图的存储结构不同、图的类型不同，都会影响创建算法 的实现细节；但是，图的总体创建流程是一致的! „ 邻接矩阵与邻接表的对比 29/106 30/106