
China-pub.com 第2章词法分析 31 下载 是标识符。其次,当串可以是单个记号也可以是若干记号的序列时,则通常解释为单个记号。 这常常被称作最长子串原理(principle of longest substring):可组成单个记号的字符的最长串 在任何时候都是假设为代表下一个记号⊙ 在使用最长子串原理时会出现记号分隔符(token delimiter)的问题,即表示那些在某时 不能代表记号的长串的字符。分隔符应是肯定为其他记号一部分的字符。例如在串 xtemp=ytemp中,等号将标识符xtemp分开,这是因为=不能作为标识符的部分出现。通常 也认为空格、新行和制表位是记号分隔符:因此wh11ex,.就解释为包含了两个记号一一保 留字w11e和带有名字x的标识符,这是因为一个空格将两个字符串分开。在这种情况下,定 义空白格伪记号非常有用0它与注释伪记号相类似,但注释伪记号仅仅是在扫描程序内部区分 其他记号。实际上,注释本身也经常作为分隔符,因此例如C代码片段 表示的就是两个保留字do和if,而不是标识符doif。 程序设计语言中的空白格伪记号的典型定义是: whitespace-(newlinel blank I tab l comment)+ 其中,等号右边的标识符代表恰当的字符或串。请注意:空白格通常不是作为记号分隔符,而 是被忽略掉。指定这个行为的语言叫作自由格式语言(free format)。除自由格式语言之外还可 以是一些诺如FORTRAN的周定格式语言,以及名种使用缩排格式的语言,例如诚位规 (offside rule)(参见“注意与参考” 一节)。自由格式语言的扫描程序必须在检查任意记号分 隔功能之后舍弃掉空白格。 分隔符结束记号串,但它们并不是记号本身的一部分。因此,扫描程序必须处理先行 (lookahead)问题:当它遇到一个分隔符时,它必须作出安排分隔符不会从输入的其他部分中 别除,方法是将分隔符返回到输入串(“备份”)或在将字符从输入中删除之前先行。在大多数 情况下,只有单个字符才需要这样做(“单个字符先行”)。例如在串xtemp=ytemp中,当遇 到=时,就可找到标识符xt©mP的结尾,且=必须保留在输入中,这是因为它表示要识别下一 个记号。还应注意,在识别记号时可能不需要使用先行。例如,等号可能是以=开头的唯一字 符,此时无需考虑下一个字符就可立即识别出它了。 有时语言可能要求不仅仅是单个字符先行,且扫描程序必须准各好可以备份任意多个字符。 在这种情况下,输入字符的缓冲和为追踪而标出位置就给扫描程序的设计带来了问题(本章后 面将会讨论到其中的一些问题)。 FORTRAN是一个并不遵守上面所谈的诸多原则的典型语言。它是固定格式语言,它的空 白格在翻译开始之前已由预处理器删除了。因此,下面的FORTRAN行 在编译器中就是 IF (X2.EQ.0)THEN 所以空白格再也不是分隔符了。FORTRAN中也没有保留字,故所有的关键字也可以是标识符, 输入每行中字符串的位置对于确定将要识别的记号十分重要。例如,下面代码行在FORTRAN 中是完全正确的: IF(I日,EQ,0)THENTHEN=1,0 日有时这也称作“最大咀嚼”定理
是标识符。其次,当串可以是单个记号也可以是若干记号的序列时,则通常解释为单个记号。 这常常被称作最长子串原理(principle of longest substring):可组成单个记号的字符的最长串 在任何时候都是假设为代表下一个记号 。 在使用最长子串原理时会出现记号分隔符( token delimiter)的问题,即表示那些在某时 不能代表记号的长串的字符。分隔符应是肯定为其他记号一部分的字符。例如在串 x t e m p = y t e m p中,等号将标识符 x t e m p分开,这是因为=不能作为标识符的部分出现。通常 也认为空格、新行和制表位是记号分隔符:因此 while x...就解释为包含了两个记号——保 留字w h i l e和带有名字x的标识符,这是因为一个空格将两个字符串分开。在这种情况下,定 义空白格伪记号非常有用 0它与注释伪记号相类似,但注释伪记号仅仅是在扫描程序内部区分 其他记号。实际上,注释本身也经常作为分隔符,因此例如 C代码片段: do / ** / if 表示的就是两个保留字d o和i f,而不是标识符d o i f。 程序设计语言中的空白格伪记号的典型定义是: whitespace = (newline | blank | tab | c o m m e n t) + 其中,等号右边的标识符代表恰当的字符或串。请注意:空白格通常不是作为记号分隔符,而 是被忽略掉。指定这个行为的语言叫作自由格式语言( free format)。除自由格式语言之外还可 以是一些诸如 F O RT R A N的固定格式语言,以及各种使用缩排格式的语言,例如越位规则 (o ffside rule)(参见“注意与参考”一节)。自由格式语言的扫描程序必须在检查任意记号分 隔功能之后舍弃掉空白格。 分隔符结束记号串,但它们并不是记号本身的一部分。因此,扫描程序必须处理先行 (l o o k a h e a d)问题:当它遇到一个分隔符时,它必须作出安排分隔符不会从输入的其他部分中 删除,方法是将分隔符返回到输入串(“备份”)或在将字符从输入中删除之前先行。在大多数 情况下,只有单个字符才需要这样做(“单个字符先行”)。例如在串x t e m p = y t e m p中,当遇 到=时,就可找到标识符 x t e m p的结尾,且=必须保留在输入中,这是因为它表示要识别下一 个记号。还应注意,在识别记号时可能不需要使用先行。例如,等号可能是以 =开头的唯一字 符,此时无需考虑下一个字符就可立即识别出它了。 有时语言可能要求不仅仅是单个字符先行,且扫描程序必须准备好可以备份任意多个字符。 在这种情况下,输入字符的缓冲和为追踪而标出位置就给扫描程序的设计带来了问题(本章后 面将会讨论到其中的一些问题)。 F O RT R A N是一个并不遵守上面所谈的诸多原则的典型语言。它是固定格式语言,它的空 白格在翻译开始之前已由预处理器删除了。因此,下面的 F O RT R A N行 I F ( X 2 . EQ. 0 ) THE N 在编译器中就是 I F ( X 2 . E Q . 0 ) T H E N 所以空白格再也不是分隔符了。F O RT R A N中也没有保留字,故所有的关键字也可以是标识符, 输入每行中字符串的位置对于确定将要识别的记号十分重要。例如,下面代码行在 F O RT R A N 中是完全正确的: IF(IF.EQ.0 )THENTHEN=1.0 第 2章 词 法 分 析 3 1 下载 有时这也称作“最大咀嚼”定理

32 编译原理及实践 China-pub.Co 下载 第1个Ir和TEN都是关键字,而第2个Ir和TEN则是表示变量的标识符。这样的结果是 FORTRAN的扫描程序必须能够追综代码行中的任意位置。例如: D099r=1.10 它引起循环体为第99行代码的循环。在Pascal中,则表示为£。x1:=1t。1呙一方面, 若将逗号改为句号: D099I=1,10 就将代码的含义完全改变了:它将值1.1赋给了名字为D099r的变量。因此,扫描程序只有到 它接触到逗号(句号)时才能得出起始的D0。在这种情况下,它可能只得追踪到行的开头并 且由此开始。 2.3有穷自动机 有穷自动机,或有穷状态的机器,是描述(或“机器”)特定类型算法的数学方法。特别 地,有穷自动机可用作描述在输入串中识别模式的过程,因此也能用作构造扫描程序。当然有 穷自动机与正则表达式之间有着很密切的关系,在下一节中大家将会看到如何从正则表达式中 构造有穷自动机。但在学习有穷自动机之前,先看一个说明的示例。 通过下面的正则表达式可在程序设计语言中给出标识符模式的一般定义(假设已定义了 letter和digit): identifier letter letterl digit) 它代表以一个字母开头且其后为任意字母和/或数字序列的串。识别这样的一个串的过程可表 示为图2-1。在此图中,标明数字1和2的圆圈 表示的是状态(state),它们表示其中记录已 被发现的模式的数量在识别过程中的位置。 带有箭头的线代表由记录一个状态向另一个 digit 状态的转换(transition),该转换依赖于所标 字符的匹配。在较简单的图示中,状态1是初 图21标识符的有穷自动机 始状态(start state)或识别过程开始的状态。 按照惯例,初始状态表示为一个“不来自任何地方”且指向它的未作标识的箭头线。状态2代 表有一单个字母已被匹配的点(表示为从状态1到状态2的转换,且其上标有1ett©x)。 一日 位于状态2中,就可看到任何数量的字母和/或数字,它们的匹配又使我们回到了状态2。代表 识别过程结束的状态称作接受状态(accepting state),当位于其中时就可说明成功了,在图中 它表示为在状态的边界画出双线。它们可能不只一个。在上面的例图中,状态2就是一个接受 状态,它表示在看到一个字母之后,随后的任何字母和数字序列(也包括根本没有)都表示一 个正规的标识符 将真实字符串识别为标识符的过程现在可通过列出在识别过程中所用到的状态和转换的序 列来表示。例如,将xtep识别为标识符的过程可表示为: .1x2±.2°2m2卫.2 在此图中,用在每一步中匹配的字母标出了每一个转换。 2.3.1确定性有穷自动机的定义 因为上面所示的例图很方便地展示出算法过程,所以它对于有穷自动机的描述很有用处
第1个I F和T H E N都是关键字,而第 2个I F和T H E N则是表示变量的标识符。这样的结果是 F O RT R A N的扫描程序必须能够追踪代码行中的任意位置。例如: D O 9 9 I = 1 , 1 0 它引起循环体为第9 9行代码的循环。在P a s c a l中,则表示为for i := 1 to 10 。另一方面, 若将逗号改为句号: D O 9 9 I = 1 . 1 0 就将代码的含义完全改变了:它将值 1 . 1赋给了名字为D O 9 9 I的变量。因此,扫描程序只有到 它接触到逗号(句号)时才能得出起始的 D O。在这种情况下,它可能只得追踪到行的开头并 且由此开始。 2.3 有穷自动机 有穷自动机,或有穷状态的机器,是描述(或“机器”)特定类型算法的数学方法。特别 地,有穷自动机可用作描述在输入串中识别模式的过程,因此也能用作构造扫描程序。当然有 穷自动机与正则表达式之间有着很密切的关系,在下一节中大家将会看到如何从正则表达式中 构造有穷自动机。但在学习有穷自动机之前,先看一个说明的示例。 通过下面的正则表达式可在程序设计语言中给出标识符模式的一般定义(假设已定义了 l e t t e r和d i g i t): identifier = letter ( letter | d i g i t) * 它代表以一个字母开头且其后为任意字母和 / 或数字序列的串。识别这样的一个串的过程可表 示为图2 - 1。在此图中,标明数字 1和2的圆圈 表示的是状态(s t a t e),它们表示其中记录已 被发现的模式的数量在识别过程中的位置。 带有箭头的线代表由记录一个状态向另一个 状态的转换(t r a n s i t i o n),该转换依赖于所标 字符的匹配。在较简单的图示中,状态 1是初 始状态(start state)或识别过程开始的状态。 按照惯例,初始状态表示为一个“不来自任何地方”且指向它的未作标识的箭头线。状态 2代 表有一单个字母已被匹配的点(表示为从状态 1到状态2的转换,且其上标有 l e t t e r)。一旦 位于状态2中,就可看到任何数量的字母和 / 或数字,它们的匹配又使我们回到了状态2。代表 识别过程结束的状态称作接受状态( accepting state),当位于其中时就可说明成功了,在图中 它表示为在状态的边界画出双线。它们可能不只一个。在上面的例图中,状态 2就是一个接受 状态,它表示在看到一个字母之后,随后的任何字母和数字序列(也包括根本没有)都表示一 个正规的标识符。 将真实字符串识别为标识符的过程现在可通过列出在识别过程中所用到的状态和转换的序 列来表示。例如,将x t e m p识别为标识符的过程可表示为: →1→ x 2→ t 2→ e 2→ m 2→ p 2 在此图中,用在每一步中匹配的字母标出了每一个转换。 2.3.1 确定性有穷自动机的定义 因为上面所示的例图很方便地展示出算法过程,所以它对于有穷自动机的描述很有用处。 3 2 编译原理及实践 下载 图2-1 标识符的有穷自动机

China-pub.com 第2章词法分析 33 下载 但是偶尔还需使用有穷自动机的更正式的描述,现在就给出一个数学定义。但绝大数情况并不 需要这么抽象,且在大多数示例中也只使用示意图。有穷自动机还有其他的描述,尤其是表格, 表格对于将算法转换成运行代码很有用途。在需要它的时候我们将会谈到它。 另外读者还需注章:我们一直在讨论的是确定性的(deterministic)有穷自动机,即:下 一个状态由当前状态和当前输入字符唯一给出的自动机。非确定性的有穷自动机是由它产生的 本节稍后将谈到它。 定义:DFA(确定性有穷自动机)M由字母表∑、状态集合S、转换函数T:SXΣ一S、 初始状态s,∈S以及接受状态的集合AcS组成。由M接受的且写作L()被定义为字符 cC,c串的集合,其中每个c,∈∑,存在状态s,=T(5,c,,3,=T,C)2,5,=了 (s,c,),其中5,是A(即一个接受状态)的一个元素。 有关这个定义请注意以下几点。S×∑指的是S和Σ的笛卡尔积或叉积:集合对(,c),其 中s∈S且c∈∑。如果有一个标为c的由状态s到状态s'的转换,则函数T记录转换:T(s,c)=s'。 与M相应的示图片段如下: 当接受状态序列3,=T5,c,b3=T(5,c,,5=T5,c,)存在,且5是一个接受状态 时,它表示如下所示的意思: →5095152 在DFA的定义和标识符示例的图示之间有许多区别。首先,在标识符图中的状态使用了据 字,而定义并未用数字对状态集合作出限制。实际上可以为状态使用任何标识系统,这其中也 包括了名字。例如:下图与图21完全一样: 在这里就称作状态start(因为它是初始状态)和in_id(因为我们发现了一个字母并识别 其后的任何字母和数字后面的标识符)。这个图示中的状态集合现在变成了{start, inid),而不是{1,2】了。 图示与定义的第2个区别在于转换不是用字符标出而是表示为字符集合的名字。例如,名 字1 etter表示根据以下正则定义的字母表中的任意字母: 1 etter▣【a-za-z1 因为如要为每个小写字母和每个大写字母画出总共52个单独的转换非常麻烦,所以这是定义的 一个便利的扩展。本章后面还会用到这个定义的扩展。 图示与定义的第3个区别更为重要:定义将转换表示为一个函数T:S×∑一S。这意味着 T(s,c)必须使每个s和c都有一个值。但在图中,只有当c是字母时,才定义T(stat,c):而 也只有当c是字母或数字时,才定义T(m_id,c)。那么,所丢失的转换跑到哪里去了呢?答案 是它们表示了出错一一即在识别标识符时,我们不能接受除来自初始状态之外的任何字符以及
但是偶尔还需使用有穷自动机的更正式的描述,现在就给出一个数学定义。但绝大数情况并不 需要这么抽象,且在大多数示例中也只使用示意图。有穷自动机还有其他的描述,尤其是表格, 表格对于将算法转换成运行代码很有用途。在需要它的时候我们将会谈到它。 另外读者还需注意:我们一直在讨论的是确定性的( d e t e r m i n i s t i c)有穷自动机,即:下 一个状态由当前状态和当前输入字符唯一给出的自动机。非确定性的有穷自动机是由它产生的。 本节稍后将谈到它。 定义:D FA(确定性有穷自动机)M由字母表å、状态集合S、转换函数T:S×å→S、 初始状态s 0ÎS以及接受状态的集合A S组成。由M接受的且写作L (M) 被定义为字符 c1 c2 . . . cn 串的集合,其中每个ci Îå,存在状态s 1 = T (s 0 , c1 ), s 2 = T (s 1 , c2 ), . . . , s n = T (s n-1 , cn ),其中s n 是A(即一个接受状态)的一个元素。 有关这个定义请注意以下几点。 S×å指的是S 和å的笛卡尔积或叉积:集合对( s, c),其 中s Î S且c Îå。如果有一个标为c 的由状态s 到状态s ' 的转换,则函数T记录转换:T (s, c) = s' 。 与M相应的示图片段如下: 当接受状态序列s 1 = T (s 0 , c1 ), s 2 = T (s 1 , c2 ), . . . , s n = T (s n-1 , cn)存在,且s n 是一个接受状态 时,它表示如下所示的意思: 在D FA的定义和标识符示例的图示之间有许多区别。首先,在标识符图中的状态使用了数 字,而定义并未用数字对状态集合作出限制。实际上可以为状态使用任何标识系统,这其中也 包括了名字。例如:下图与图2 - 1完全一样: 在这里就称作状态 s t a r t(因为它是初始状态)和 i n _ i d(因为我们发现了一个字母并识别 其后的任何字母和数字后面的标识符)。这个图示中的状态集合现在变成了 { s t a r t , i n _ i d },而不是{ 1 , 2 }了。 图示与定义的第2个区别在于转换不是用字符标出而是表示为字符集合的名字。例如,名 字l e t t e r表示根据以下正则定义的字母表中的任意字母: letter = [ a - zA - Z ] 因为如要为每个小写字母和每个大写字母画出总共 5 2个单独的转换非常麻烦,所以这是定义的 一个便利的扩展。本章后面还会用到这个定义的扩展。 图示与定义的第 3个区别更为重要:定义将转换表示为一个函数 T:S×å→S。这意味着 T (s, c)必须使每个s 和c 都有一个值。但在图中,只有当c 是字母时,才定义T (start, c);而 也只有当c 是字母或数字时,才定义T (in_id, c)。那么,所丢失的转换跑到哪里去了呢?答案 是它们表示了出错——即在识别标识符时,我们不能接受除来自初始状态之外的任何字符以及 Ì 第 2章 词 法 分 析 3 3 下载
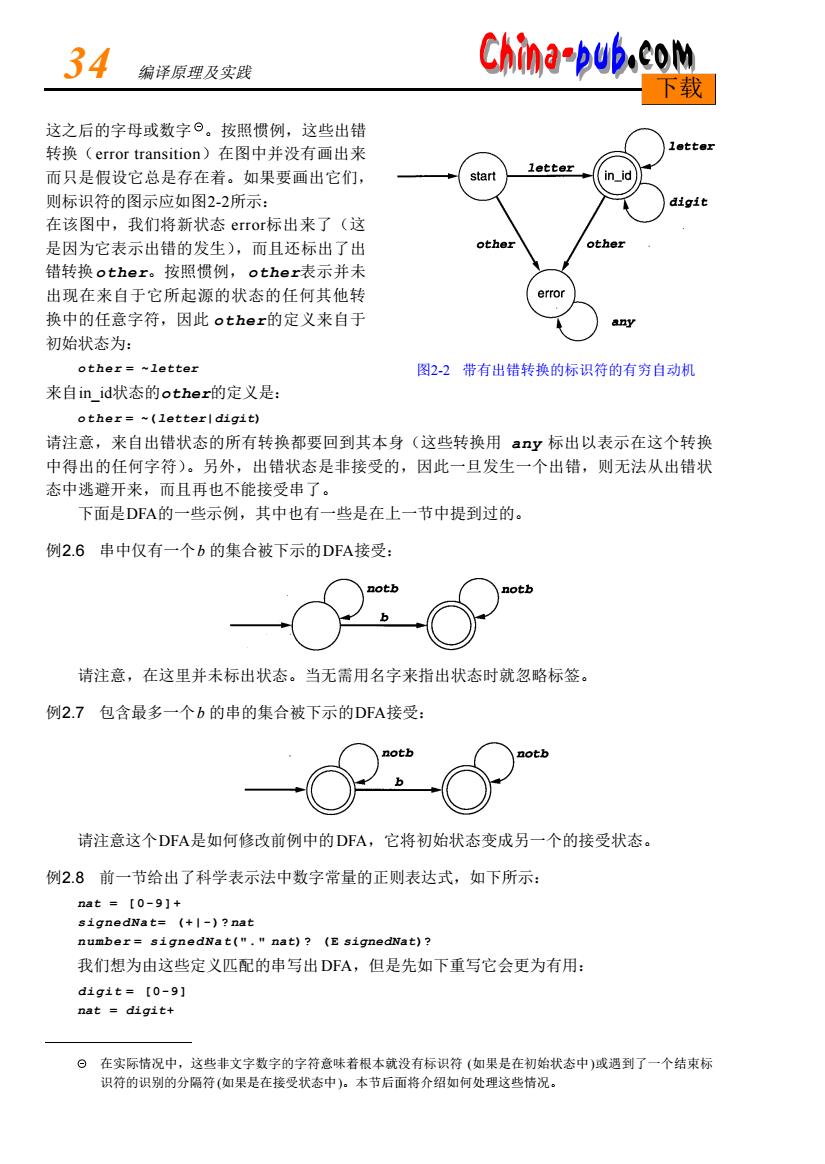
34 编译原理及实践 China-pub.com 载 这之后的字母或数字⊙。按照惯例,这些出错 转换(error transition)在图中并没有画出来 而只是假设它总是存在着。如果要画出它们, 则标识符的图示应如图2-2所示: 在该图中,我们将新状态error标出来了(这 是因为它表示出错的发生),而且还标出了出 错转换other。按照惯例,other表示并未 出现在来自于它所起源的状态的任何其他转 换中的任意字符,因此other的定义来自于 初始状态为: other=~letter 图22带有出错转换的标识符的有穷自动机 来自in_id状态的other的定义是: other=(letterl digit) 请注意,来自出错状态的所有转换都要回到其本身(这些转换用ay标出以表示在这个转换 中得出的任何字符)。另外,出错状态是非接受的,因此一旦发生一个出错,则无法从出错状 态中逃避开来,而且再也不能接受串了。 下面是DFA的一些示例,其中也有一些是在上一节中提到过的。 例2.6串中仅有一个b的集合被下示的DFA接受: not 请注意,在这里并未标出状态。当无需用名字来指出状态时就忽略标签 例2.7包含最多一个b的串的集合被下示的DFA接受: notb notb b 请注意这个DFA是如何修改前例中的DFA,它将初始状态变成另一个的接受状态。 例2.8前一节给出了科学表示法中数字常量的正则表达式,如下所示: nat=【0-9] (+1-)?na gnedNat("."nat)?(E signedNat)? 我们想为由这些定义匹配的串写出DFA,但是先如下重写它会更为有用: 日在实际情况中,这些非文字数字的字符意味着根本就没有标识符(如果是在初始状态中)或遇到了一个结束标 识符的识别的分隔符(果是在接受状态中)。本节后面将介绍如何处理这些情况
这之后的字母或数字 。按照惯例,这些出错 转换(error transition)在图中并没有画出来 而只是假设它总是存在着。如果要画出它们, 则标识符的图示应如图2 - 2所示: 在该图中,我们将新状态 e r r o r标出来了(这 是因为它表示出错的发生),而且还标出了出 错转换o t h e r。按照惯例, o t h e r表示并未 出现在来自于它所起源的状态的任何其他转 换中的任意字符,因此 o t h e r的定义来自于 初始状态为: other = ~l e t t e r 来自i n _ i d状态的o t h e r的定义是: other = ~(l e t t e r|d i g i t) 请注意,来自出错状态的所有转换都要回到其本身(这些转换用 a ny 标出以表示在这个转换 中得出的任何字符)。另外,出错状态是非接受的,因此一旦发生一个出错,则无法从出错状 态中逃避开来,而且再也不能接受串了。 下面是D FA的一些示例,其中也有一些是在上一节中提到过的。 例2.6 串中仅有一个b 的集合被下示的D FA接受: 请注意,在这里并未标出状态。当无需用名字来指出状态时就忽略标签。 例2.7 包含最多一个b 的串的集合被下示的D FA接受: 请注意这个D FA是如何修改前例中的D FA,它将初始状态变成另一个的接受状态。 例2.8 前一节给出了科学表示法中数字常量的正则表达式,如下所示: nat = [0-9]+ signedNat = (+|-)? nat number = signedNat ("." n a t)? (E s i g n e d N a t) ? 我们想为由这些定义匹配的串写出D FA,但是先如下重写它会更为有用: digit = [0-9] nat = d i g i t+ 3 4 编译原理及实践 下载 在实际情况中,这些非文字数字的字符意味着根本就没有标识符 (如果是在初始状态中)或遇到了一个结束标 识符的识别的分隔符(如果是在接受状态中)。本节后面将介绍如何处理这些情况。 图2-2 带有出错转换的标识符的有穷自动机
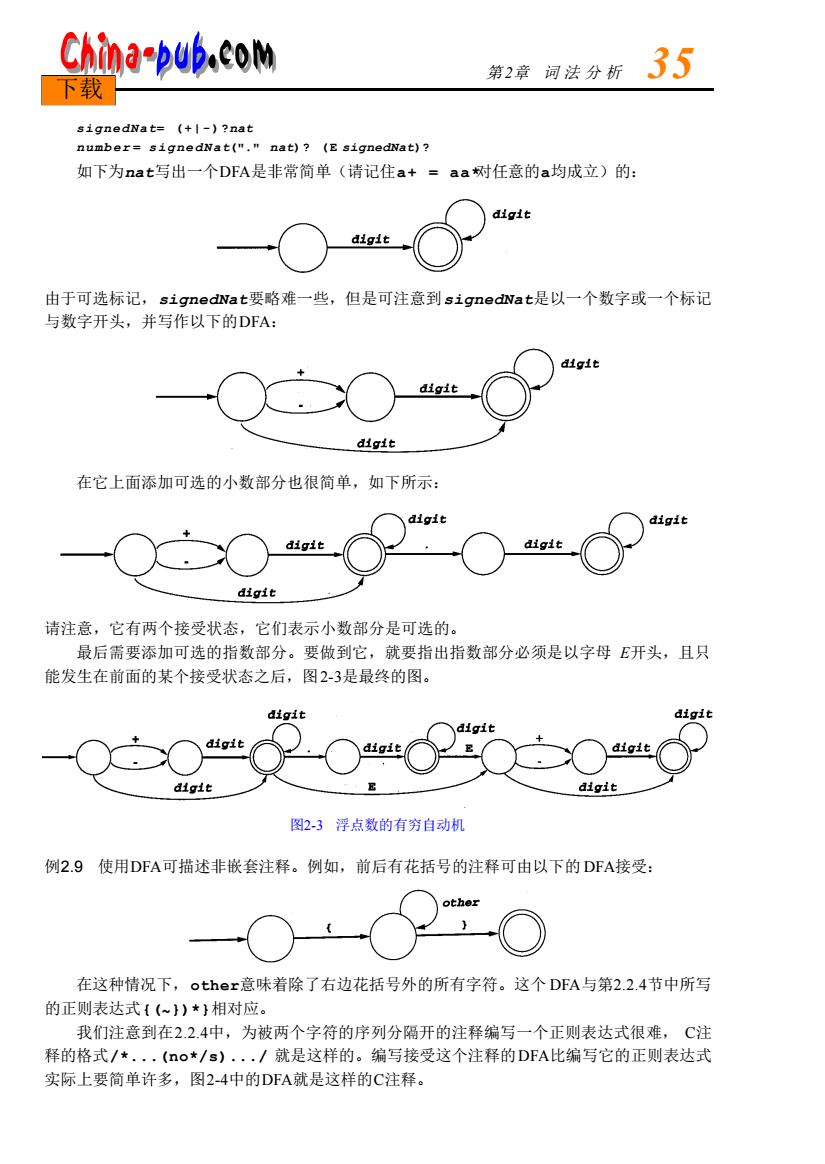
China-pub.com 下载 第2京河法分新了5 signedNat=(+1-)?nat number=signedNat("."nat)?(E signedNat)? 如下为nat写出一个DFA是非常简单(请记住a+=aa对任意的a均成立)的: digit 由于可选标记,signedNat要略难一些,但是可注意到signedNat是以一个数字或一个标记 与数字开头,并写作以下的DFA: digit 在它上面添加可选的小数部分也很简单,如下所示: digit 请注意,它有两个接受状态,它们表示小数部分是可选的。 最后需要添加可选的指数部分。要做到它,就要指出指数部分必须是以字母E开头,且只 能发生在前面的某个接受状态之后,图2-3是最终的图。 digit digit git ○.○“○2 ○ 图2-3浮点数的有穷自动机 例2.9使用DFA可描述非嵌套注释。例如,前后有花括号的注释可由以下的DFA接受: other ○ 在这种情况下,other意味着除了右边花括号外的所有字符。这个DFA与第2.2.4节中所写 的正则表达式{(~)*}相对应。 我们注意到在2.2.4中,为被两个字符的序列分隔开的注释编写一个正则表达式很难,C注 释的格式/.·.(o*/s).,/就是这样的。编写接受这个注释的DFA比编写它的正则表达式 实际上要简单许多,图2-4中的DFA就是这样的C注释
signedNat = (+|-)? n a t number = signedNat ("." n a t)? (E s i g n e d N a t) ? 如下为n a t写出一个D FA是非常简单(请记住a+ = aa*对任意的a均成立)的: 由于可选标记,s i g n e d N a t要略难一些,但是可注意到s i g n e d N a t是以一个数字或一个标记 与数字开头,并写作以下的D FA: 在它上面添加可选的小数部分也很简单,如下所示: 请注意,它有两个接受状态,它们表示小数部分是可选的。 最后需要添加可选的指数部分。要做到它,就要指出指数部分必须是以字母 E开头,且只 能发生在前面的某个接受状态之后,图2 - 3是最终的图。 图2-3 浮点数的有穷自动机 例2.9 使用D FA可描述非嵌套注释。例如,前后有花括号的注释可由以下的 D FA接受: 在这种情况下,o t h e r意味着除了右边花括号外的所有字符。这个 D FA与第2 . 2 . 4节中所写 的正则表达式{ (~} ) * }相对应。 我们注意到在2 . 2 . 4中,为被两个字符的序列分隔开的注释编写一个正则表达式很难, C注 释的格式/ * . . . ( n o * / s ) . . . / 就是这样的。编写接受这个注释的D FA比编写它的正则表达式 实际上要简单许多,图2 - 4中的D FA就是这样的C注释。 第 2章 词 法 分 析 3 5 下载