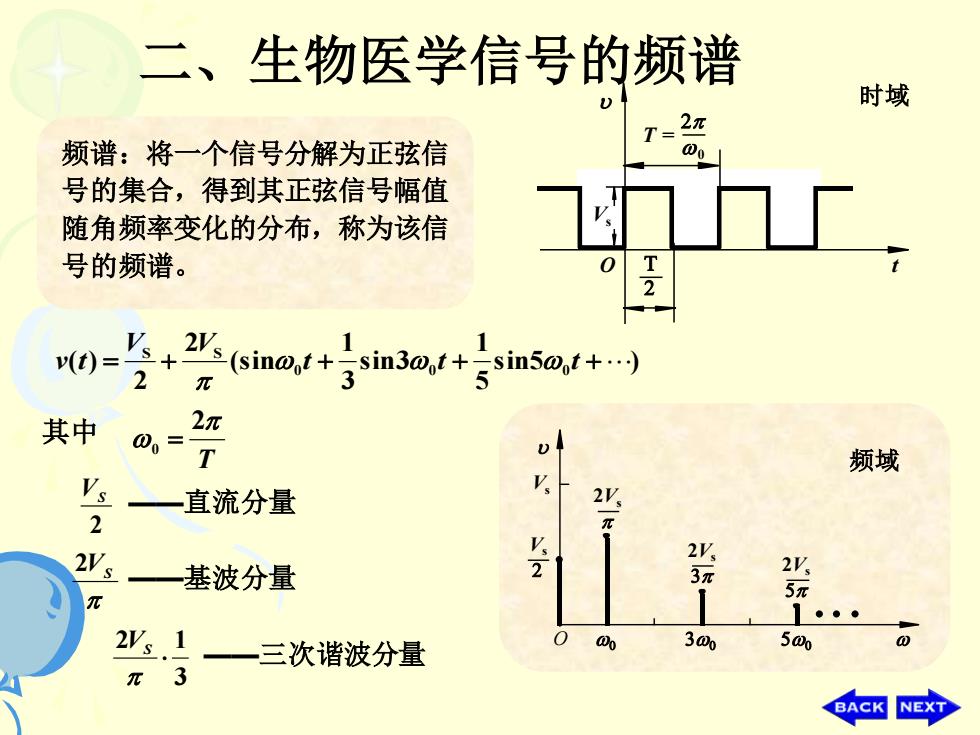
二、生物医学信号的频谱 时域 频谱:将一个信号分解为正弦信 0g1 号的集合,得到其正弦信号幅值 随角频率变化的分布,称为该信 号的频谱。 v(t)= (im.+sin3o.+sin50.t) +2 2 3 其中 2π 00= T 频域 —一直流分量 2 华 2Vs 基波分量 2 张 1。·。 2y.1 —一三次谐波分量 0 300 500 π3 BACK
B. 方波信号 sin5 ) 5 1 sin3 3 1 (sin 2 2 ( ) 0 0 0 = S + S t + t + t + V V v t T 2 0 = 时域 O 0 T = t Vs 频域 O 2Vs Vs Vs 2Vs 2Vs 满足狄利克雷条件,展开成 傅里叶级数 2 VS ——直流分量 其中 2VS ——基波分量 3 2 1 VS ——三次谐波分量 频谱:将一个信号分解为正弦信 号的集合,得到其正弦信号幅值 随角频率变化的分布,称为该信 号的频谱。 二、生物医学信号的频谱

R a波 50u V ST段 a波 动脉脉波 V 50uV P一R期间 S一T间期 8亚 QRS 04V (Q-.T间期

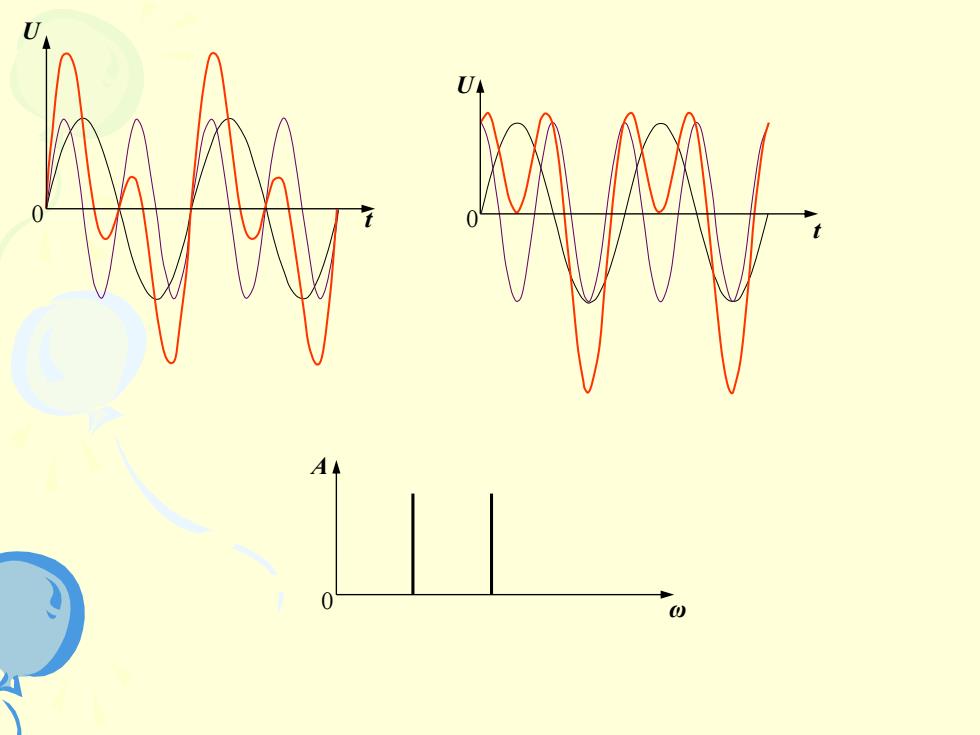
1.周期性波形的频谱 U(0=∑asin(2it+)n=0、1、2、3 n=1时,fn为f,f是非正弦式周期波的重 复频率一基频。此频率的正弦波称为基波, 其它正弦波的频率f都是基频的整数倍,称为 n倍频,相应的正弦波称为n次谐波。即n=2、3、 4.分别对应二次、三次、四次谐波,用特 性曲线来表示,一般是频谱的方法来表示
⒈ 周期性波形的频谱 U(t) =an sin(2fnt +n) n=0、1、2、3 n=1时,fn为f1,f1是非正弦式周期波的重 复频率——基频。此频率的正弦波称为基波, 其它正弦波的频率fn都是基频的整数倍,称为 n倍频,相应的正弦波称为n次谐波。即n=2、3、 4.分别对应二次、三次、四次谐波,用特 性曲线来表示,一般是频谱的方法来表示
U
U t ω A0 0 t U0

2.脉冲波形的频谱 在时间上短促的波形称为脉冲。 单个孤立的波形可以用一系列正弦波的叠 加来组成,频率取连续值,且具有连续频谱。 连续频谱的波形叠加用积分式表达: U(t)=2 Ar cos(2f+df 0
⒉ 脉冲波形的频谱 在时间上短促的波形称为脉冲。 单个孤立的波形可以用一系列正弦波的叠 加来组成,频率取连续值,且具有连续频谱。 连续频谱的波形叠加用积分式表达: = + 0 U(t) 2 Af cos(2f t f)df