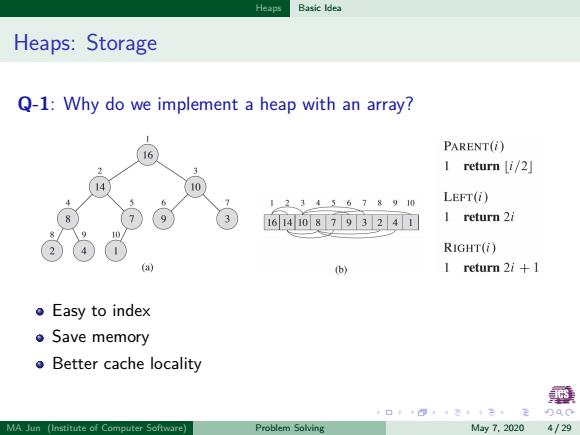
Heaps Basic Idea Heaps:Storage Q-1:Why do we implement a heap with an array? PARENT(i) 16 I return [i/2] 10 12345678910 LEFT() 1614108793241] 1 return 2i RIGHT(i) (b) 1 return 2i+1 Easy to index ●Save memory o Better cache locality 4口卡40,在是生Q0 MA Jun (Institute of Computer Software) Problem Solving My7.20204/29
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Heaps Basic Idea Heaps: Storage Q-1: Why do we implement a heap with an array? Easy to index Save memory Better cache locality MA Jun (Institute of Computer Software) Problem Solving May 7, 2020 4 / 29
Heaps Basic Idea Heaps:Height The height of a node o The number of edges on the longest simple downward path from the node to a leaf. 口卡+①,2生Q0 MA Jun (Institute of Computer Software) Problem Solving May7.20205/29
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Heaps Basic Idea Heaps: Height The height of a node The number of edges on the longest simple downward path from the node to a leaf. The height of a heap The height of its root, Θ(lg n). A heap of n elements is based on a nearly complete binary tree h=3 h=2 h=1 h=1 h=0 h=0 MA Jun (Institute of Computer Software) Problem Solving May 7, 2020 5 / 29

Heaps Basic Idea Heaps:Height The height of a node o The number of edges on the longest simple downward path from the node to a leaf. The height of a heap The height of its root,(lg n). o A heap of n elements is based on a nearly complete binary tree 16h=3 h=2 14 1oh=1 h=1 8 9 3h=0 h=0 (a) 美 MA Jun (Institute of Computer Software) Problem Solving May7.20205/29
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Heaps Basic Idea Heaps: Height The height of a node The number of edges on the longest simple downward path from the node to a leaf. The height of a heap The height of its root, Θ(lg n). A heap of n elements is based on a nearly complete binary tree h=3 h=2 h=1 h=1 h=0 h=0 MA Jun (Institute of Computer Software) Problem Solving May 7, 2020 5 / 29

Heaps Basic ldea Heaps:basic operations The MAX-HEAPIFY procedure,which runs in O(Ig n)time,is the key to main- taining the max-heap property. The BUILD-MAX-HEAP procedure,which runs in linear time,produces a max- heap from an unordered input array. The HEAPSORT procedure,which runs in O(nIgn)time,sorts an array in place. The MAX-HEAP-INSERT,HEAP-EXTRACT-MAX,HEAP-INCREASE-KEY, and HEAP-MAXIMUM procedures,which run in O(Ig n)time,allow the heap data structure to implement a priority queue. 國 ,口+45,。左,4生,2Q
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Heaps Basic Idea Heaps: basic operations MA Jun (Institute of Computer Software) Problem Solving May 7, 2020 6 / 29
Heaps Basic Idea Heaps:basic operations TheMAX-HEAPIFY procedure,which runs in O(lg n)time,is the key to main- taining the max-heap property. The BUILD-MAX-HEAP procedure,which runs in linear time,produces a max- heap from an unordered input array. The HEAPSORT procedure,which runs in O(nIgn)time,sorts an array in place. The MAX-HEAP-INSERT,HEAP-EXTRACT-MAX,HEAP-INCREASE-KEY, and HEAP-MAXIMUM procedures,which run in O(Ign)time,allow the heap data structure to implement a priority queue. 國 4口4步,,左·生,生
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Heaps Basic Idea Heaps: basic operations MA Jun (Institute of Computer Software) Problem Solving May 7, 2020 6 / 29