
2-5 Linear Recurrences Hengfeng Wei hfwei@nju.edu.cn March 26,2020 4口·¥①,43,t夏,里Q0 Hengfeng Wei (hfweixinju.edu.cn) 2-5 Linear Recurrences farch26.20201/26
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2-5 Linear Recurrences Hengfeng Wei hfwei@nju.edu.cn March 26, 2020 Hengfeng Wei (hfwei@nju.edu.cn) 2-5 Linear Recurrences March 26, 2020 1 / 26

Don't we already know how to use the "Master Theorem"? T(n)=al(n/b)+f(n) 4口,1①,43,t夏,里0Q0 Hengfeng Wei (hfweixinju.edu.cn) 2-5 Linear Recurrences farch26.20202/26
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Don’t we already know how to use the “Master Theorem”? T(n) = aT(n/b) + f(n) Linear recurrences which may arise in average-case analysis. Hengfeng Wei (hfwei@nju.edu.cn) 2-5 Linear Recurrences March 26, 2020 2 / 26

Don't we already know how to use the "Master Theorem"? T(n)=al(n/b)+f(n) Linear recurrences which may arise in average-case analysis. 4口·¥①,43,t夏,里Q0 Hengfeng Wei (hfweixinju.edu.cn) 2-5 Linear Recurrences farch26.20202/26
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Don’t we already know how to use the “Master Theorem”? T(n) = aT(n/b) + f(n) Linear recurrences which may arise in average-case analysis. Hengfeng Wei (hfwei@nju.edu.cn) 2-5 Linear Recurrences March 26, 2020 2 / 26
an f(an-1;an-2;...;an-t)+g(n) 4口·¥①,43,t夏,里Q0 Hengfeng Wei (hfweixinju.edu.cn) 2-5 Linear Recurrences farch26.20203/26
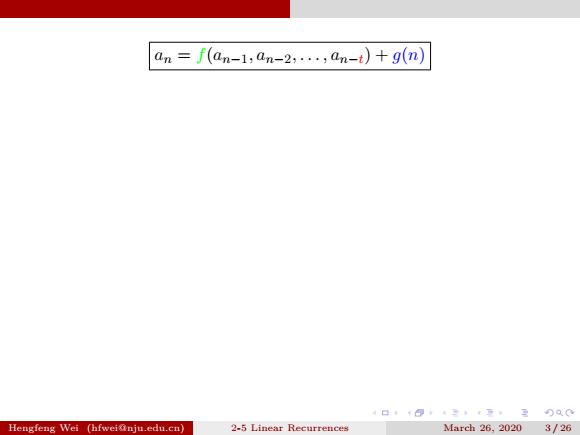
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . an = f(an−1, an−2, . . . , an−t) + g(n) Hengfeng Wei (hfwei@nju.edu.cn) 2-5 Linear Recurrences March 26, 2020 3 / 26

an f(an-1;an-2;...;an-t)+g(n) recurrence type typical example first-order linear an nan-1-1 nonlinear am=1/(1+an-1) second-order linear an=0m-1十2an-2 nonlinear am=am-1an-2十Vam-2 variable coefficients am=nan-1+(n-1)am-2+1 tth order an=f(am-1,am-2,·,0n-t)】 full-history 0n=n十an-1十an-2..十a1 divide-and-conquer an aln/2]amn/21+n Table 2.1 Classification of recurrences 4口·1①,43,t夏,30Q0 Hengfeng Wei (hfweixinju.edu.cn) 2-5 Linear Recurrences farch26.20203/26
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . an = f(an−1, an−2, . . . , an−t) + g(n) Hengfeng Wei (hfwei@nju.edu.cn) 2-5 Linear Recurrences March 26, 2020 3 / 26