
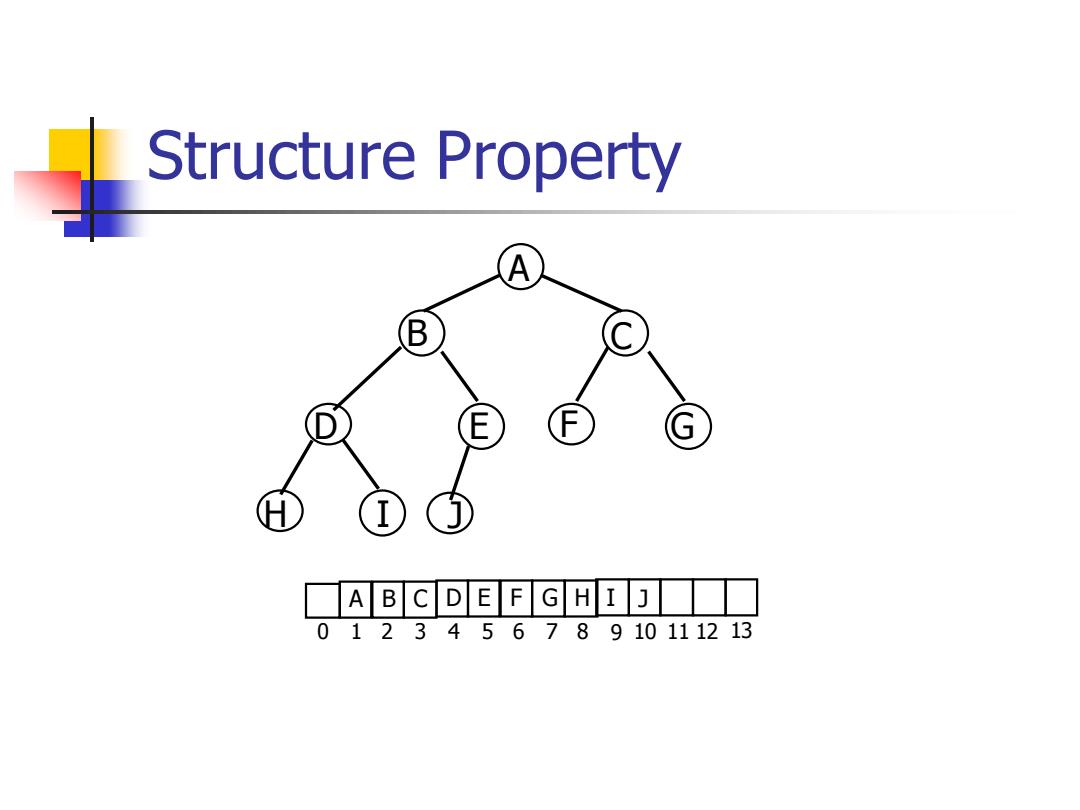
Structure Property An important observation is that because a complete binary tree is so regular,it can be represented in an array and no pointers are necessary. a For any element in array position /the left child is in position 2/the right child is in the cell after that left child (24+1),and the parent is in position L//2
Structure Property ◼ An important observation is that because a complete binary tree is so regular, it can be represented in an array and no pointers are necessary. ◼ For any element in array position i, the left child is in position 2i, the right child is in the cell after that left child (2i+1), and the parent is in position i/2
Structure Property A B E G A B CDE F GH I J 012345678910111213
Structure Property A B C D E F G H I J 0 1 2 3 4 5 6 7 8 9 10 11 12 13 D E B C A F G H I J

Structure Property Thus,not only are pointers not required,but the operations required to traverse the tree are extremely simple and likely to be very fast on most computers. The only problem with this implementation is that an estimate of the maximum heap size is required in advance. A heap data structure will then consist of an array (of whatever type the key is)and an integer representing the maximum and current heap sizes. Figure 6.4 shows a typical priority queue declaration
Structure Property ◼ Thus, not only are pointers not required, but the operations required to traverse the tree are extremely simple and likely to be very fast on most computers. ◼ The only problem with this implementation is that an estimate of the maximum heap size is required in advance. ◼ A heap data structure will then consist of an array (of whatever type the key is) and an integer representing the maximum and current heap sizes. ◼ Figure 6.4 shows a typical priority queue declaration
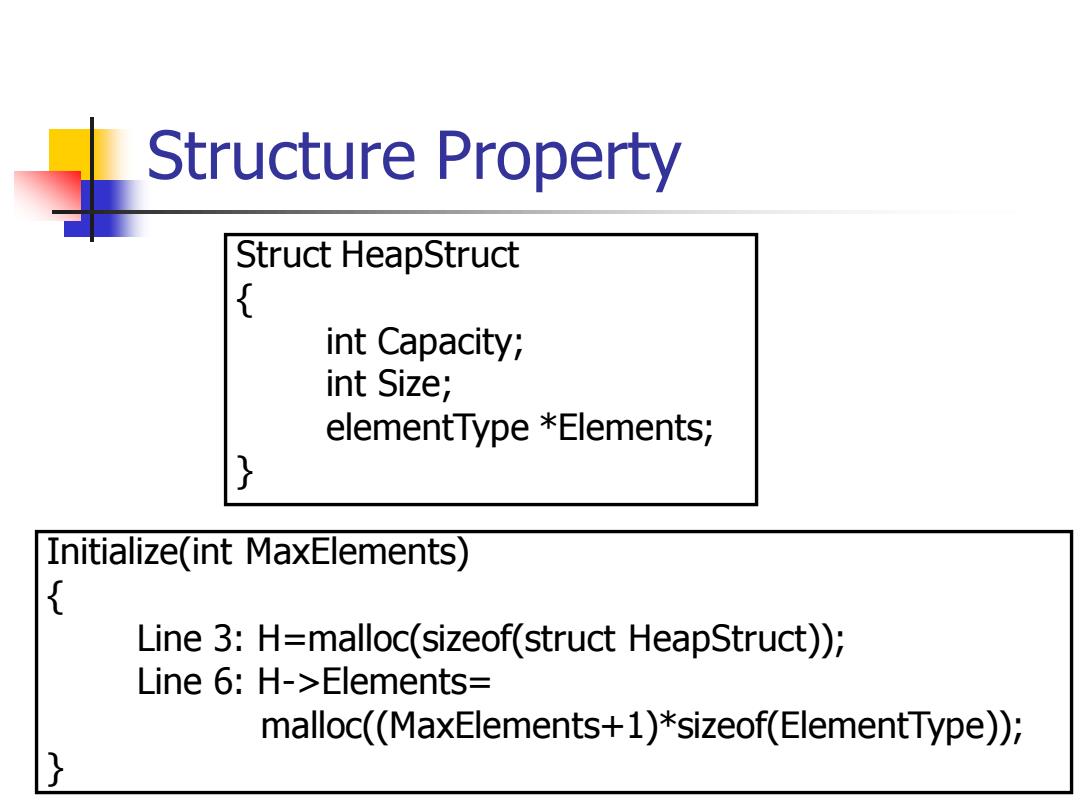
Structure Property Struct HeapStruct { int Capacity; int Size; elementType *Elements; Initialize(int MaxElements) { Line 3:H=malloc(sizeof(struct HeapStruct)); Line 6:H->Elements= malloc((MaxElements+1)*sizeof(ElementType)); }
Structure Property Struct HeapStruct { int Capacity; int Size; elementType *Elements; } Initialize(int MaxElements) { Line 3: H=malloc(sizeof(struct HeapStruct)); Line 6: H->Elements= malloc((MaxElements+1)*sizeof(ElementType)); }

Heap Order Property The property that allows operations to be performed quickly is the heap order property. Since we want to be able to find the minimum quickly, it makes sense that the smallest element should be at the root. If we consider that any subtree should also be a heap, then any node should be smaller than all of its descendants
Heap Order Property ◼ The property that allows operations to be performed quickly is the heap order property. ◼ Since we want to be able to find the minimum quickly, it makes sense that the smallest element should be at the root. ◼ If we consider that any subtree should also be a heap, then any node should be smaller than all of its descendants