杠杆定律 随着结晶过程的进行,合金中各相的成分及其相 对量都将发生变化。杠杆定律可解决相的成分和相对 量的变化问题。 a L+a 7TT7T刀 图5-10杠杆定律证明及力学比喻
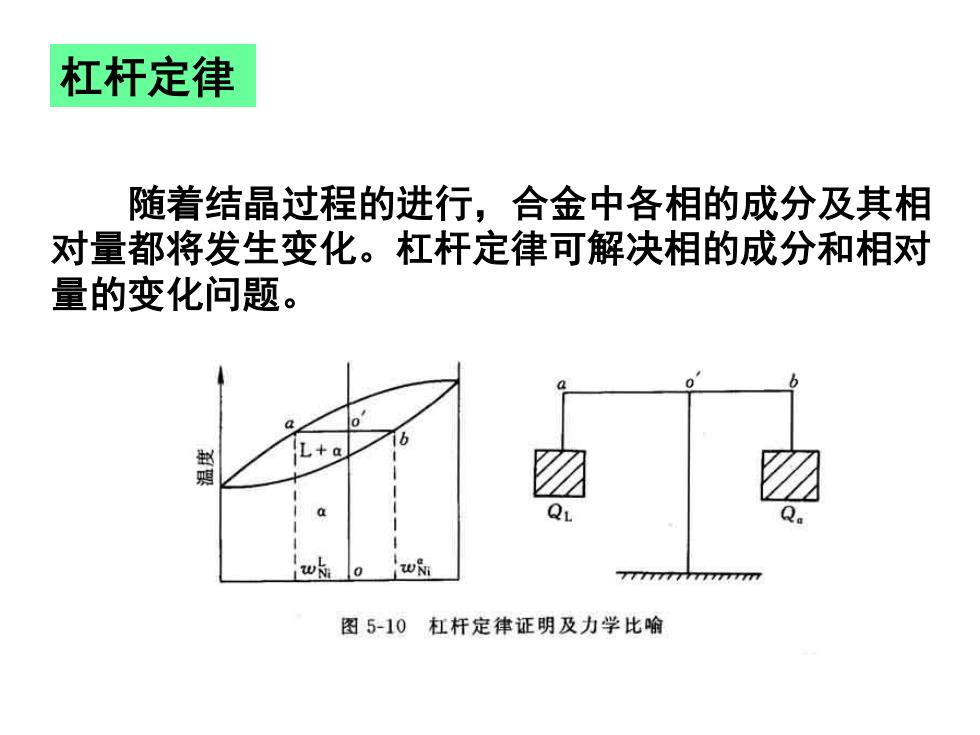
杠杆定律 随着结晶过程的进行,合金中各相的成分及其相 对量都将发生变化。杠杆定律可解决相的成分和相对 量的变化问题
证明:设成分为o的合金在t温度时,液、固两相平衡共存,两 相的成分点分别为a、b,对应的横坐标值为W、wa。 设合金的总质量为Qo,液相质量为Q,固 相质量为Qa,则有 Qo=QL+Qa L+ 液相中镍的质量为QwL,固相中镍的质量 为QaWa,合金中镍的质量为Qowo。 2oWo=OLWL+OaWa =(g。-Qa)hwz+0awe 整理得 Cu WL Wa ge=w-wLx100%.gL=1"。-0x100% Co Wa-Wi Co Wa-WL 又 2o(Wa-wo)-C:(Wo-WL)
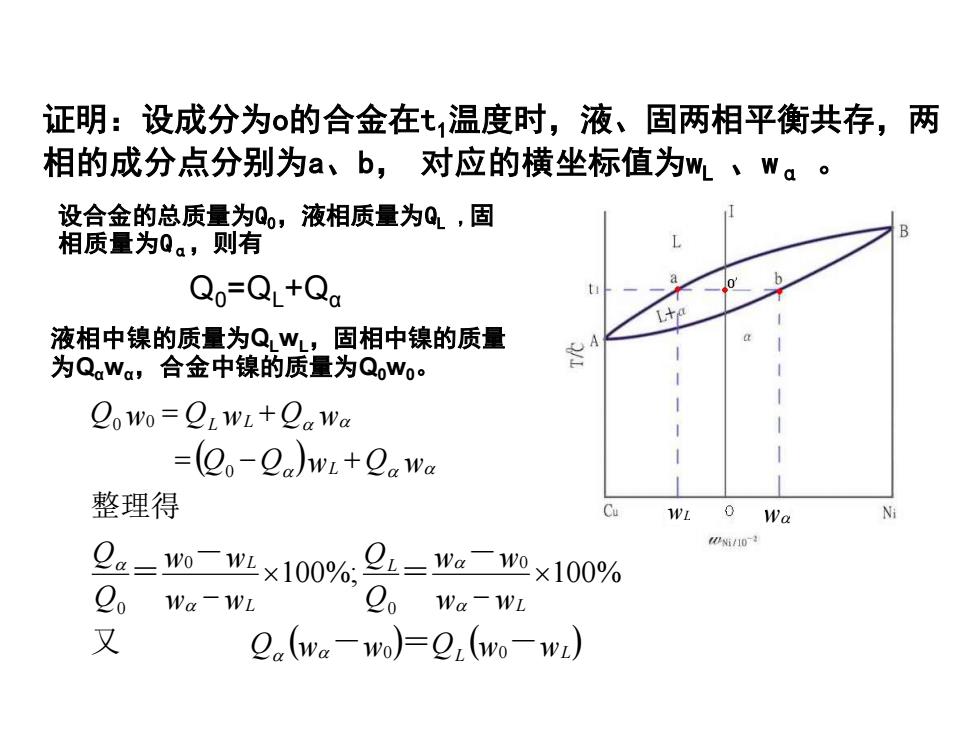
设合金的总质量为Q0,液相质量为QL ,固 相质量为Qα,则有 Q0=QL+Qα 液相中镍的质量为QLwL,固相中镍的质量 为Qαwα,合金中镍的质量为Q0w0。 ( ) Q (w w ) Q (w w ) w w w w Q Q w w w w Q Q Q Q w Q w Q w Q w Q w L L L L L L L L L 又 - = - - = - = 整理得 0 0 0 0 0 0 0 0 0 100%; 100% − − = − + = + ( ) Q (w w ) Q (w w ) w w w w Q Q w w w w Q Q Q Q w Q w Q w Q w Q w L L L L L L L L L 又 - = - - = - = 整理得 0 0 0 0 0 0 0 0 0 100%; 100% − − = − + = + ( ) Q (w w ) Q (w w ) w w w w Q Q w w w w Q Q Q Q w Q w Q w Q w Q w L L L L L L L L L 又 - = - - = - = 整理得 0 0 0 0 0 0 0 0 0 100%; 100% − − = − + = + 证明:设成分为o的合金在t1温度时,液、固两相平衡共存,两 相的成分点分别为a、b, 对应的横坐标值为wL 、wα
两平衡相的成分(杠杆的两个端点)、平均成分(杠杆 的支点)、质量分数三者之间符合杠杆原理 2.0'b=9,ao' 杠杆规则示意图 杠杆定律只适用于处于平衡状态的两相区
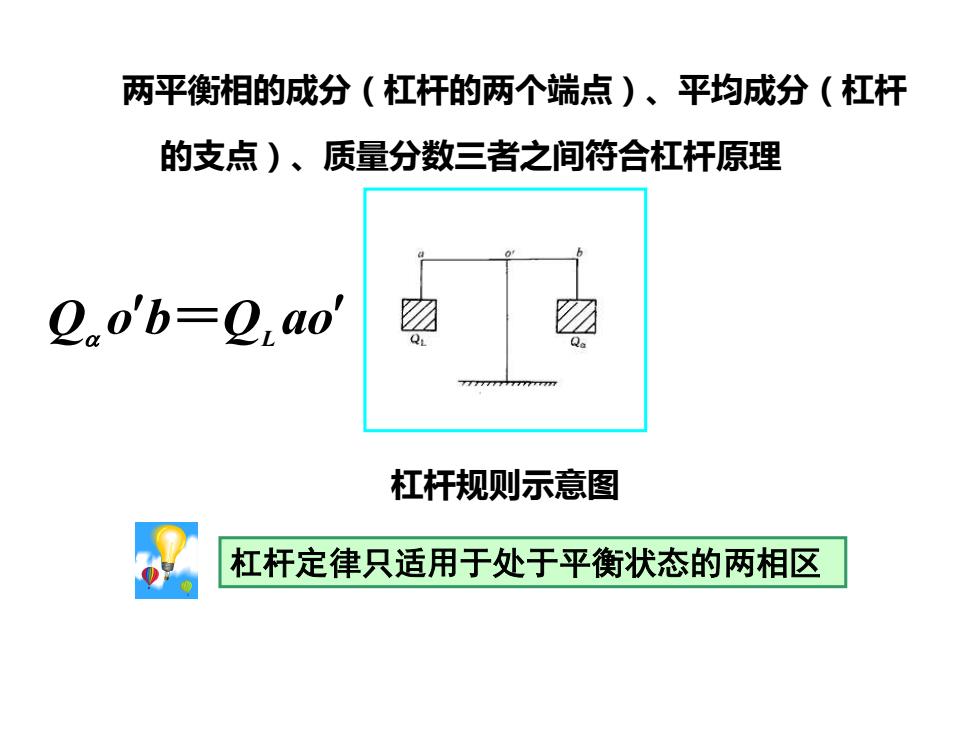
杠杆规则示意图 杠杆定律只适用于处于平衡状态的两相区 Q o b=QL ao 两平衡相的成分(杠杆的两个端点)、平均成分(杠杆 的支点)、质量分数三者之间符合杠杆原理
例题 例:下图为一匀晶相图,试根据相图确定: 1)w=0.40的合金开始凝固出来的固相成分为多少? 2)若开始凝固出来的固体成分为w=0.60,合金的成分为多少? 3)成分为ω0.70的合金最后凝固时的液体成分为多少? 4)若合金成分为ωB0.50,凝固到某温度时液相成分w0.40, 固相成分为ω0.80,此时液相和固相的相对量为多少? 1/℃ L+a 0.20 0.40 0.60 0.80B
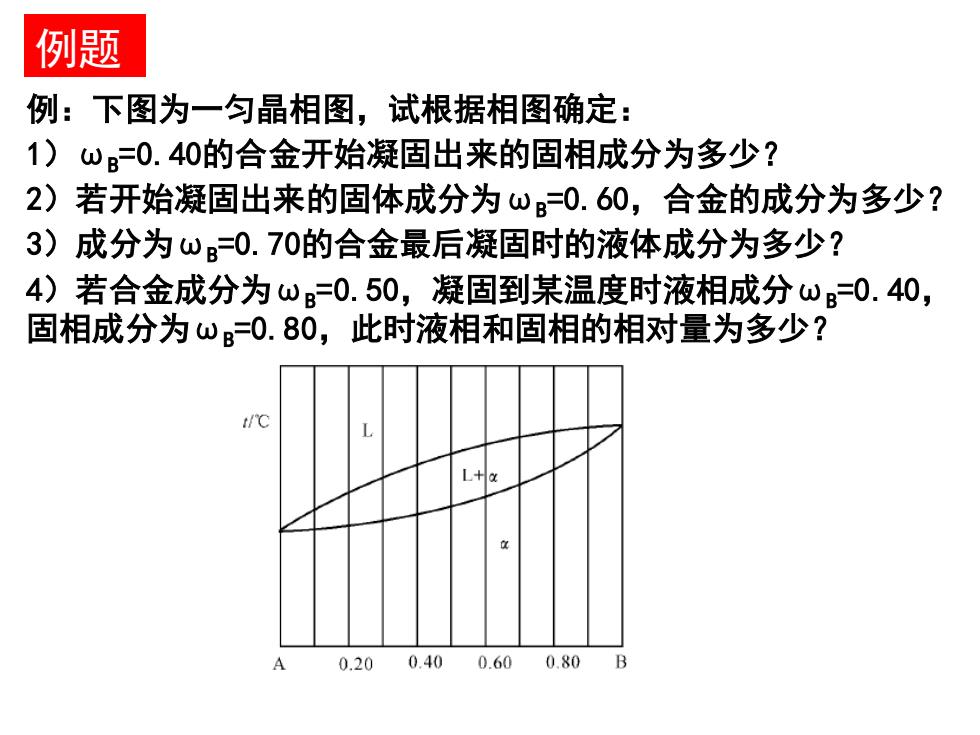
例:下图为一匀晶相图,试根据相图确定: 1)ωB=0.40的合金开始凝固出来的固相成分为多少? 2)若开始凝固出来的固体成分为ωB=0.60,合金的成分为多少? 3)成分为ωB=0.70的合金最后凝固时的液体成分为多少? 4)若合金成分为ωB=0.50,凝固到某温度时液相成分ωB=0.40, 固相成分为ωB=0.80,此时液相和固相的相对量为多少? 例题

3)固溶体的不平衡结晶 非平衡凝固:指液态凝固时冷却速度过快,原子来 不及充分扩散,在凝固过程中合金的成分得不到完 全均匀的凝固过程。 通常,原子在液态中的扩散速度远大于在固态中的 扩散速度,因此可假定原子在液相中能充分扩散, 并使液相成分完全均匀,固相成分不均匀
3)固溶体的不平衡结晶 非平衡凝固:指液态凝固时冷却速度过快,原子来 不及充分扩散,在凝固过程中合金的成分得不到完 全均匀的凝固过程。 通常,原子在液态中的扩散速度远大于在固态中的 扩散速度,因此可假定原子在液相中能充分扩散, 并使液相成分完全均匀,固相成分不均匀