
授课教案 第八章光波调制 (8.13)称为菲涅耳椭球,(8.14)称为折射率椭球(有的应用领域称为光率体)。 折射率椭球是描述光学性质最常用几何图形,一般把其表达式写作 2+y+= (8.15) 61826 或 (8.16) 这是一个归一化的D空间的椭球,其三个主轴方向就是介电主轴方向。 §8-3电光效应 施加电场之后,引起束缚电荷的重新分布,导致离子晶格的微小形变,其结 果将引起介电系数的变化,最终导致晶体折射率的变化。折射率成为外加电场E 的函数,即 △n=n-nm=GE+c2E2+ (8.17) 线性电光效应或泡克耳(Pockels)效应:折射率的改变与外加电场大小成正比。 二次电光效应或克尔(Kr)效应:折射率的改变与外加电场强度的平方成正比。 对大多数电光晶体材料,一次效应要比二次效应显著,可略去二次项。只有 在对称类型的晶体中,因不存在一次电光效应,二次效应才比较明显。 引入电场的方式: (1)纵向电光效应:电场方向与光束传播方向平行 (2)横向电光效应:电场方向与光束传播方向垂直 一线性电光效应 采用几何图形——折射率椭球体的方法分析。 晶体未加外电场时,主轴坐标系中,晶体折射率椭球方程为 (8.18) n,,n:为折射率椭球的主折射率。 当晶体施加电场后,其折射率椭球就发生“变形”,椭球方程变为 得)+得+日+*,*)18 由于外电场,折射率椭球各系数(1/㎡随之发生线性变化,其变化量可定义为
授课教案 第八章 光波调制 (8.13)称为菲涅耳椭球,(8.14)称为折射率椭球(有的应用领域称为光率体)。 折射率椭球是描述光学性质最常用几何图形,一般把其表达式写作 1 3 2 2 2 1 2 =++ εεε zyx (8.15) 或 1 2 3 2 2 2 2 2 1 2 =++ n z n y n x (8.16) 这是一个归一化的 D 空间的椭球,其三个主轴方向就是介电主轴方向。 §8-3 电光效应 施加电场之后,引起束缚电荷的重新分布,导致离子晶格的微小形变,其结 果将引起介电系数的变化,最终导致晶体折射率的变化。折射率成为外加电场 E 的函数,即 ++=−= L (8.17) 2 Δ 210 EcEcnnn 线性电光效应或泡克耳(Pockels)效应:折射率的改变与外加电场大小成正比。 二次电光效应或克尔(Kerr)效应:折射率的改变与外加电场强度的平方成正比。 对大多数电光晶体材料,一次效应要比二次效应显著,可略去二次项。只有 在对称类型的晶体中,因不存在一次电光效应,二次效应才比较明显。 引入电场的方式: (1)纵向电光效应:电场方向与光束传播方向平行 (2)横向电光效应:电场方向与光束传播方向垂直 一 线性电光效应 采用几何图形——折射率椭球体的方法分析。 晶体未加外电场时,主轴坐标系中,晶体折射率椭球方程为 1 2 2 2 2 2 2 2 3 2 2 2 2 2 1 2 =++=++ zyx n z n y n x n z n y n x (8.18) nx,ny,nz为折射率椭球的主折射率。 当晶体施加电场后,其折射率椭球就发生“变形”,椭球方程变为 1 1 2 1 2 1 2 1 1 1 6 2 5 2 4 2 2 3 2 2 2 2 2 1 2 ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ + ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ + ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ + ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ + ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ + ⎠ ⎞ ⎜ ⎝ ⎛ xy n xz n yz n z n y n x n (8.19) 由于外电场,折射率椭球各系数(1/n 2 )随之发生线性变化,其变化量可定义为 6
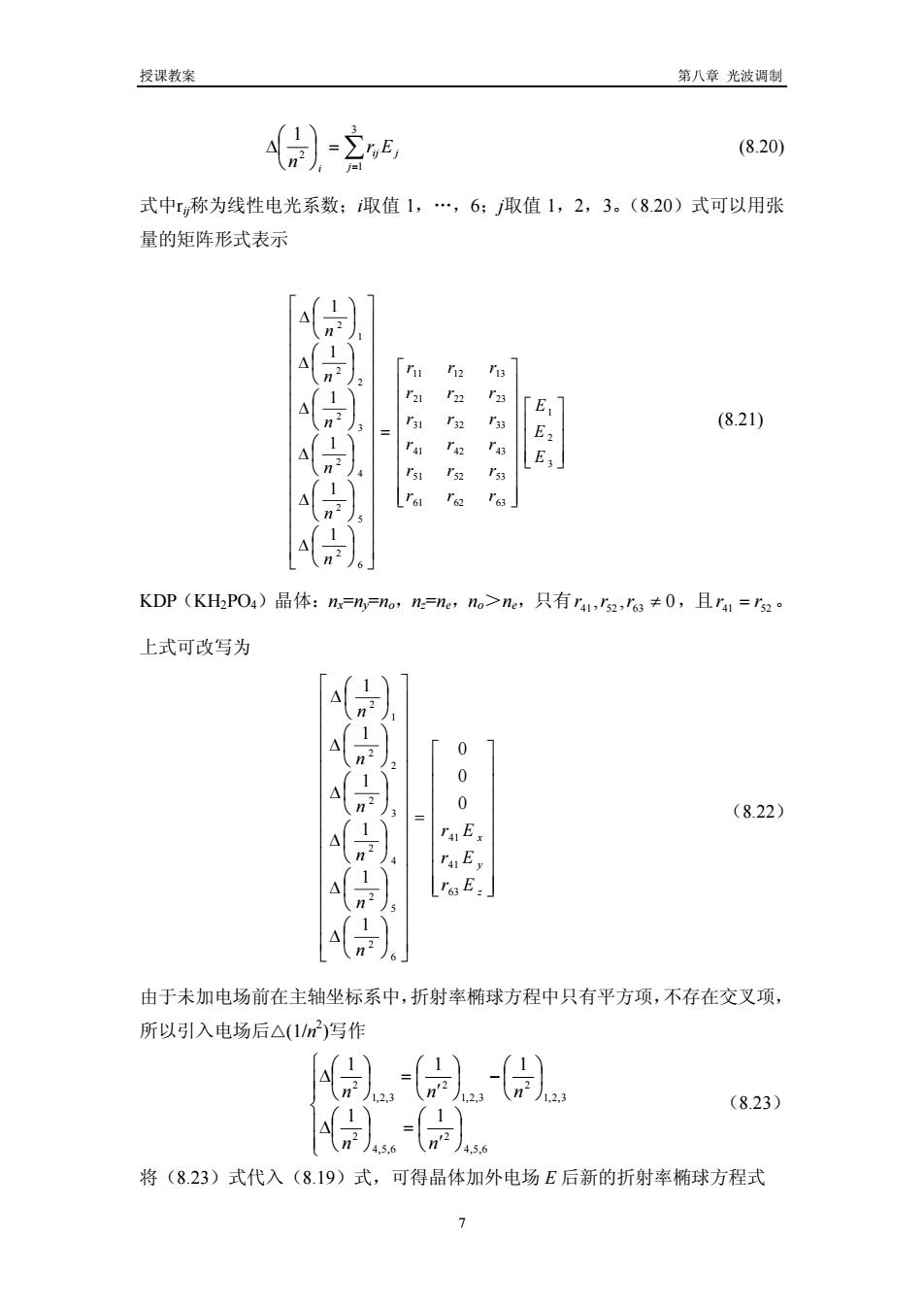
授课教案 第八章光波调制 得)-立6 (8.20) 式中r称为线性电光系数:取值1,,6:取值1,2,3。(8.20)式可以用张 量的矩阵形式表示 4/ 合 (8.21) E KDP(KHPO)晶体:n=n,=o,m=ne,no>me,只有r1,52,a≠0,且r=r 上式可改写为 A 0 (8.22) raEs 由于未加电场前在主轴坐标系中,折射率椭球方程中只有平方项,不存在交叉项, 所以引入电场后△(1m写作 4) 123 (8.23) 将(8.23)式代入(8.19)式,可得晶体加外电场E后新的折射率椭球方程式 >
授课教案 第八章 光波调制 ∑= ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ Δ 3 1 2 1 j jij i Er n (8.20) 式中rij称为线性电光系数;i取值 1,…,6;j取值 1,2,3。(8.20)式可以用张 量的矩阵形式表示 ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ 3 2 1 61 62 63 51 52 53 41 42 43 31 32 33 21 22 23 11 12 13 6 2 5 2 4 2 3 2 2 2 1 2 1 1 1 1 1 1 E E E rrr rrr rrr rrr rrr rrr n n n n n n (8.21) KDP(KH2PO4)晶体:nx=ny=no,nz=ne,no>ne,只有 0,, rrr 635241 ≠ ,且 = rr 5241 。 上式可改写为 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ z y x Er Er Er n n n n n n 63 41 41 6 2 5 2 4 2 3 2 2 2 1 2 0 0 0 1 1 1 1 1 1 (8.22) 由于未加电场前在主轴坐标系中,折射率椭球方程中只有平方项,不存在交叉项, 所以引入电场后△(1/n 2 )写作 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ′ ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ Δ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ − ⎠ ⎞ ⎜ ⎝ ⎛ ′ ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ Δ 6,5,4 2 6,5,4 2 3,2,1 2 3,2,1 2 3,2,1 2 1 1 1 1 1 n n n n n (8.23) 将(8.23)式代入(8.19)式,可得晶体加外电场 E 后新的折射率椭球方程式 7

授课教案 第八章光波调制 元+元+7+2,+2比,+2E.=1 x2y2.z2 (824) 1.外加电场的方向平行于z轴 即E=E,E=E,0,上式变为 x2 +元+元+2,= (8.25) 为寻找新的感应主轴坐标系(x,y,)使得椭球方程(8.25)不含交叉项, 将x坐标和y坐标绕:轴旋转a角且当α=45时,感应主轴坐标系中的椭球方程 为 (8.26) n 近似处理后可得 ny -n,nraE. (8.27 图8.6加电场后折射率椭球的变化 (1)晶体由单轴晶体变成了双轴晶体。 (2)折射率椭球的主轴绕:轴旋转了45°角,此转角与外加电场大小无关,其 折射率变化与电场成正比。 2.外加电场的方向平行于x轴 即E=E,E=E,=0,(8.24)式变为 (8.28) 按下图进行坐标轴变换后,可得
授课教案 第八章 光波调制 41 41 63 1222 2 2 2 2 2 2 x y +++++ z = eoo xyErxzEryzEr n z n y n x (8.24) 1. 外加电场的方向平行于 z 轴 即Ez=E,Ex=Ey=0,上式变为 63 12 2 2 2 2 2 2 +++ z = eoo xyEr n z n y n x (8.25) 为寻找新的感应主轴坐标系(x′,y′,z′)使得椭球方程(8.25)不含交叉项, 将 x 坐标和 y 坐标绕 z 轴旋转α角且当α =45°时,感应主轴坐标系中的椭球方程 为 1 1 1 1 2 2 2 2 63 2 2 63 ′ + ′ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ′ −+ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + z n yEr n xEr n e z o z o (8.26) 近似处理后可得 ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ = += −= ′ ′ ′ ez oy zo ox zo nn Ernnn Ernnn 63 3 63 3 2 1 2 1 (8.27) 图 8.6 加电场后折射率椭球的变化 (1) 晶体由单轴晶体变成了双轴晶体。 (2) 折射率椭球的主轴绕 z 轴旋转了 45°角,此转角与外加电场大小无关,其 折射率变化与电场成正比。 2. 外加电场的方向平行于 x 轴 即Ex=E,Ex=Ey=0,(8.24)式变为 2 41 1 2 2 2 2 2 2 +++ x = eoo yzE n z n y n x γ (8.28) 按下图进行坐标轴变换后,可得 8
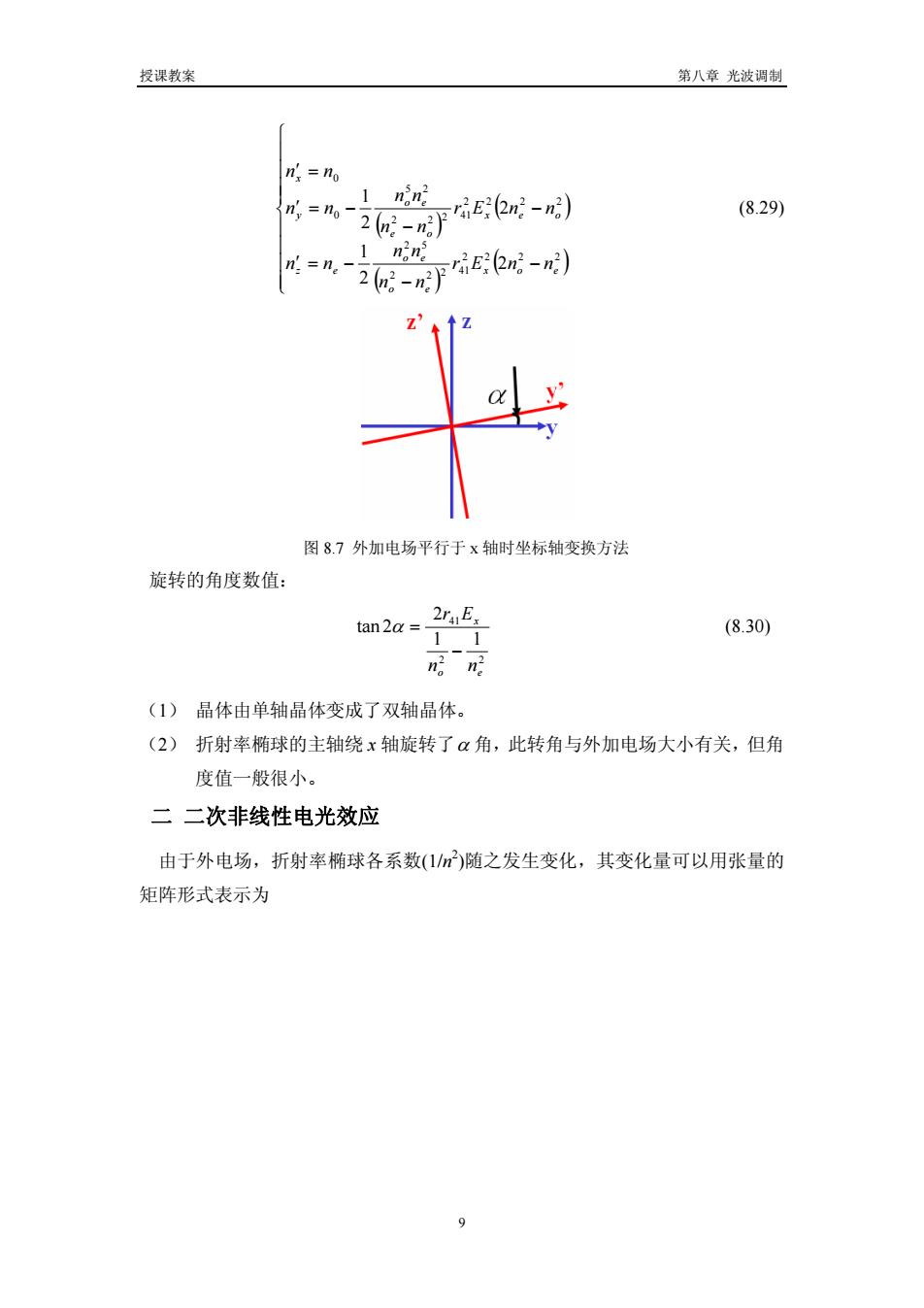
授课教案 第八章光波调制 m=。-2优- (829) 图8.7外加电场平行于x轴时坐标轴变换方法 旋转的角度数值: tan2a=- 2r41E (8.30) ngn园 (1)晶体由单轴晶体变成了双轴晶体。 (2)折射率椭球的主轴绕x轴旋转了α角,此转角与外加电场大小有关,但角 度值一般很小。 二二次非线性电光效应 由于外电场,折射率椭球各系数(1随之发生变化,其变化量可以用张量的 矩阵形式表示为 9
授课教案 第八章 光波调制 ( ) ( ) ( ) ( ) ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ − − ′ −= − − ′ −= ′ = 2222 2 41 22 52 2222 2 41 22 25 0 0 2 2 1 2 2 1 eox eo eo ez oex oe eo y x nnEr nn nn nn nnEr nn nn nn nn (8.29) 图 8.7 外加电场平行于 x 轴时坐标轴变换方法 旋转的角度数值: 22 41 11 2 2tan eo x nn Er − α = (8.30) (1) 晶体由单轴晶体变成了双轴晶体。 (2) 折射率椭球的主轴绕 x 轴旋转了α 角,此转角与外加电场大小有关,但角 度值一般很小。 二 二次非线性电光效应 由于外电场,折射率椭球各系数(1/n 2 )随之发生变化,其变化量可以用张量的 矩阵形式表示为 9