
决策树:C4.5 口信息增益率 Gain ratio(D,a)= Gain(D,a) IV(a) (4.3) 其中 (4.4) 称为属性a的“固有值”(intrinsic value)[Quinlan,l993l.属性a的可能 取值数目越多(即V越大),则V(a)的值通常会越大. 增益率准则对可取值数目较少的属性有所偏好 著名的C4.5决策树算法综合了信息增益准则和信息率准则的特 点:先从候选划分属性中找出信息增益高于平均水平的属性,再从 中选择增益率最高的。 电子科技大学研究生《模式识别》
电子科技大学研究生《模式识别》 增益率准则对可取值数目较少的属性有所偏好 著名的C4.5决策树算法综合了信息增益准则和信息率准则的特 点:先从候选划分属性中找出信息增益高于平均水平的属性,再从 中选择增益率最高的。 决策树:C4.5 o 信息增益率

决策树:CART 5 数据集D的纯度可用“基尼值”来度量 GiniD)-2∑Pe=1-》G 1D 反映了从D中随机抽 取两个样本,其类别 k=1k≠k k=1 标记不一致的概率 Gini(D)越小,数据集的纯度越高 口属性的基尼指数定义为: Gini index(D,a)v Gini(D) 应选择那个使划分后基尼指数最小的属性作为最优划分 属性,即 0*= argmin Gini index(D,a) a∈A CART [Breiman et al,19s4采用“基尼指数”来选择划分属性 电子科技大学研究生《模式识别》
电子科技大学研究生《模式识别》 决策树:CART o 数据集 的纯度可用“基尼值”来度量 越小,数据集 的纯度越高 o 属性 的基尼指数定义为: o 应选择那个使划分后基尼指数最小的属性作为最优划分 属性,即 o CART [Breiman et al., 1984]采用“基尼指数”来选择划分属性 反映了从 中随机抽 取两个样本,其类别 标记不一致的概率
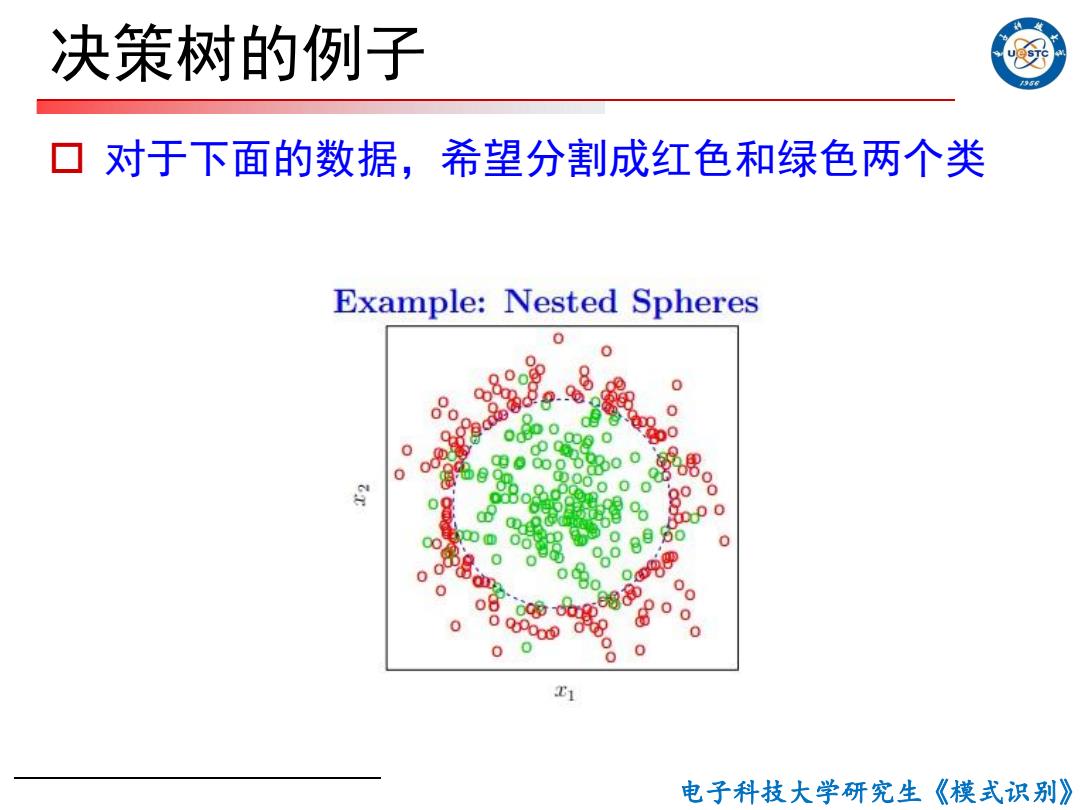
决策树的例子 56 对于下面的数据,希望分割成红色和绿色两个类 Example:Nested Spheres ● 0 电子科技大学研究生《模式识别》
电子科技大学研究生《模式识别》 决策树的例子 o 对于下面的数据,希望分割成红色和绿色两个类
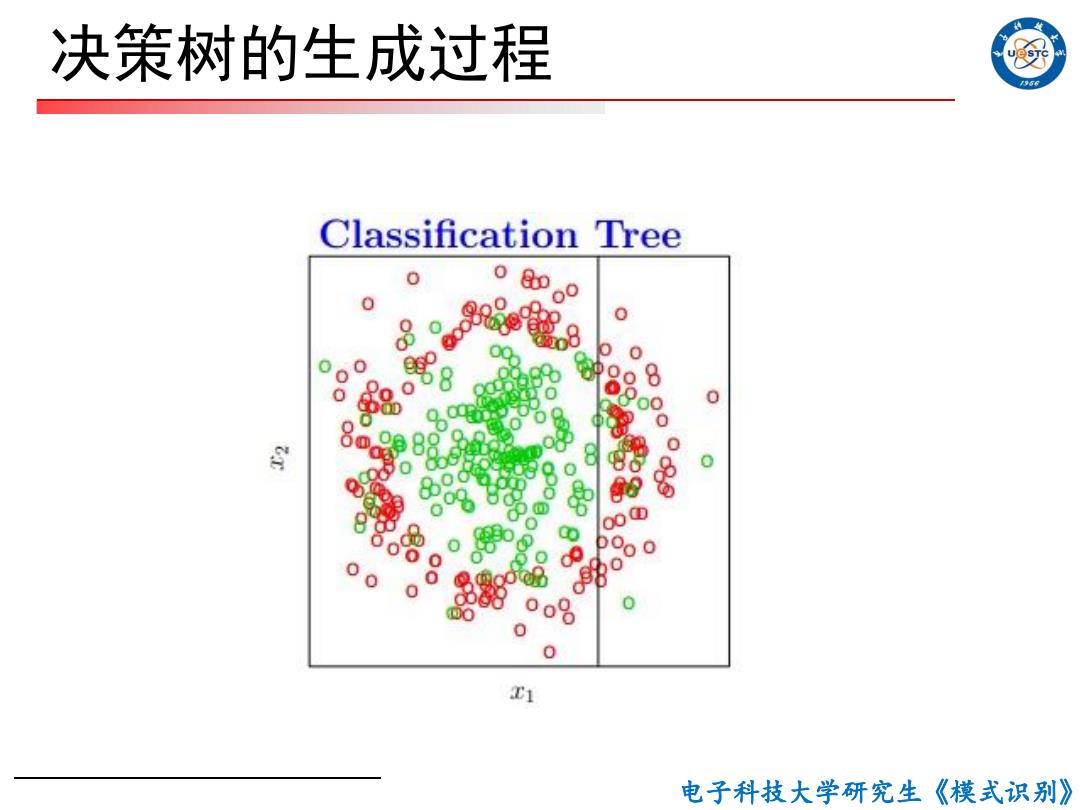
决策树的生成过程 956 Classification Tree 0 0 0 含 气M 0 00 0 0 o% 0 0 1 电子科技大学研究生《模式识别》
电子科技大学研究生《模式识别》 决策树的生成过程
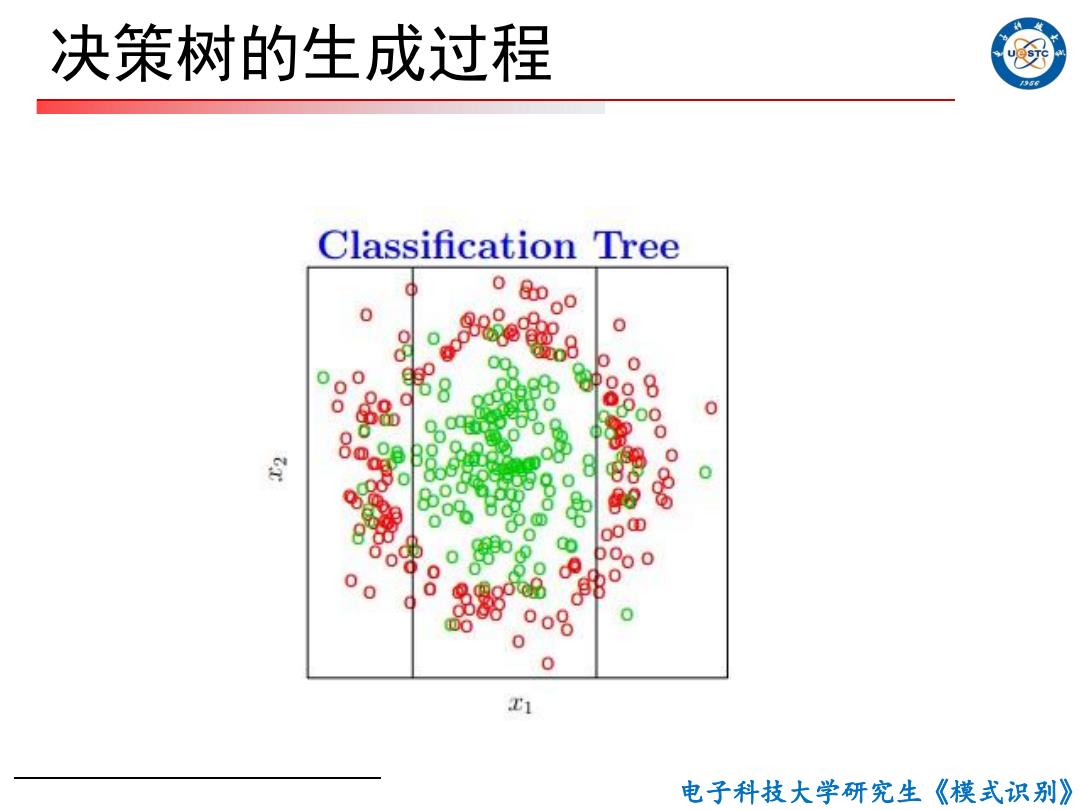
决策树的生成过程 956 Classification Tree 0 0 800 0 850 ① 0 0 00 0 o8 0 T1 电子科技大学研究生《模式识别》
电子科技大学研究生《模式识别》 决策树的生成过程