
决策问题 例 956 顾客编号 年龄 性别 月收入 是否购买 1 21 男 4000 否 汽车销售店客户情况的例子 2 33 女 5000 否 3 30 女 3800 否 4 38 女 2000 否 5 25 男 7000 否 6 32 女 2500 否 7 20 女 2000 否 8 26 女 9000 是 9 32 男 5000 是 10 24 男 7000 否 11 40 女 4800 否 12 28 男 2800 否 13 35 女 4500 否 14 33 男 2800 是 15 37 男 4000 是 16 31 女 2500 否 电子科技大学研究生《模式识别》
电子科技大学研究生《模式识别》 决策问题
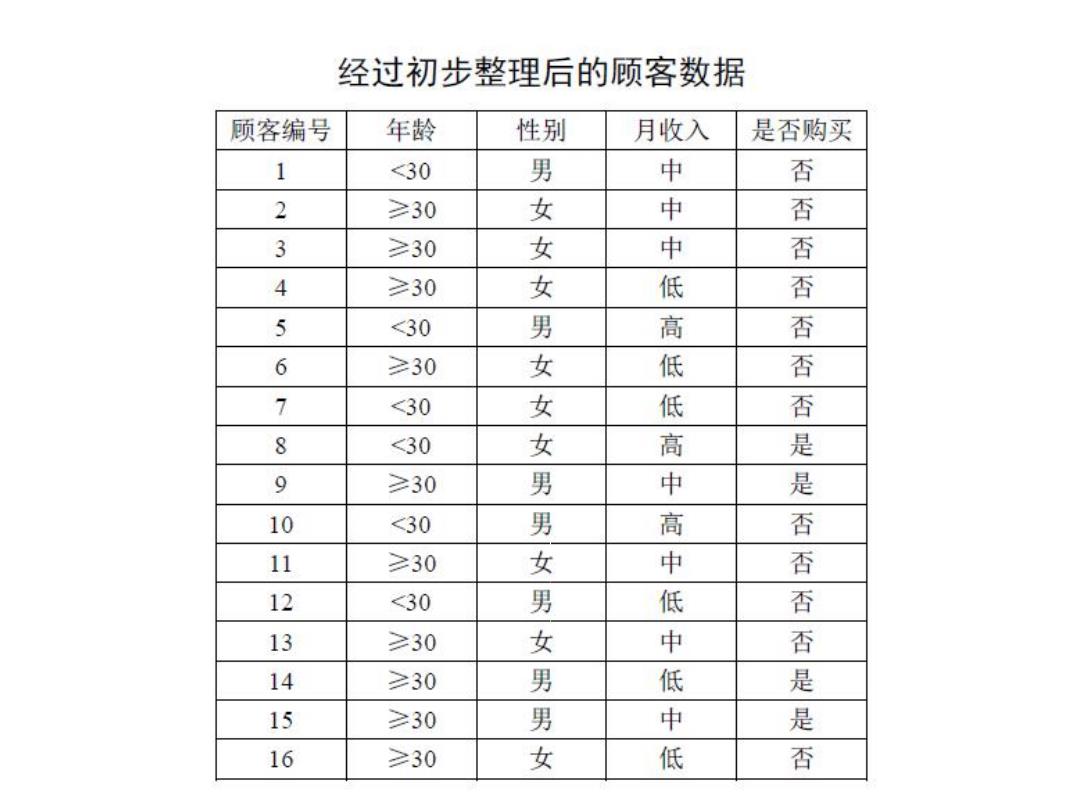
经过初步整理后的顾客数据 顾客编号 年龄 性别 月收入 是否购买 1 <30 男 中 否 2 ≥30 女 中 否 3 ≥30 女 中 否 4 ≥30 女 低 否 5 <30 男 高 否 6 ≥30 女 低 否 7 <30 女 低 否 8 <30 女 高 是 9 ≥30 男 中 是 10 <30 男 高 否 11 ≥30 女 中 否 12 <30 男 低 否 13 ≥30 女 中 否 14 ≥30 男 低 是 15 ≥30 男 中 是 16 ≥30 女 低 否
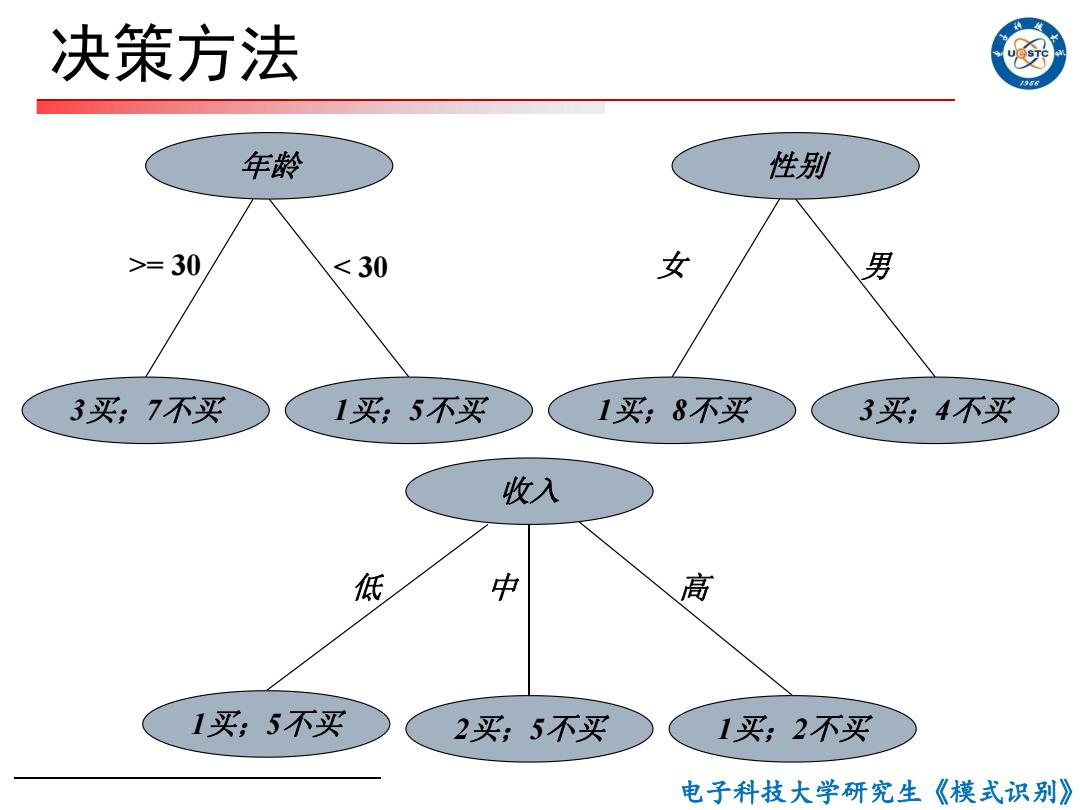
决策方法 年龄 性别 >=30 <30 女 男 3买;7不买 1买;5不买 1买,8不买 3买;4不买 收入 低 中 高 1买;5不买 2买;5不买 1买;2不买 电子科技大学研究生《模式识别》
电子科技大学研究生《模式识别》 决策方法 年龄 3买;7不买 1买;5不买 >= 30 < 30 性别 1买;8不买 3买;4不买 女 男 收入 1买;5不买 2买;5不买 低 高 1买;2不买 中

决策树 ▣概念 按树结构来决策,希望分支结点所包含的样本尽可能 属于同一类别,即结,点的“纯度”越来越高,可以高效地 从根结点到达叶结,点,得到决策结果。 口关键? ■纯度:属性如何做最优划分 三种度量结点“纯度”的指标: 1.信息增益 2.增益率 3.基尼指数 电子科技大学研究生《模式识别》
电子科技大学研究生《模式识别》 o 概念 o 关键? n 纯度:属性如何做最优划分 按树结构来决策,希望分支结点所包含的样本尽可能 属于同一类别,即结点的“纯度”越来越高,可以高效地 从根结点到达叶结点,得到决策结果。 三种度量结点“纯度”的指标: 1. 信息增益 2. 增益率 3. 基尼指数 决策树

决策树:D3 信息熵:平均而言发生一个事件我们得到的信息量 大小。所以数学上,信息熵其实是信息量的期望。 口特征X的熵: 熵:表示随机变量的不确定性。变量不 H(X)=->P;logpa 确定性越高,熵越高。 2=1 口条件熵:在一个条件下,阝 随机变量的不确定性。 特征X的信息增益:信息增益=entroy(前)- entroy(后) IG(X=H(c)-H(c X) 电子科技大学研究生《模式识别》
电子科技大学研究生《模式识别》 o 信息熵:平均而言发生一个事件我们得到的信息量 大小。所以数学上,信息熵其实是信息量的期望。 o 特征X的熵: o 条件熵:在一个条件下,随机变量的不确定性。 o 特征X的信息增益 :信息增益 = entroy(前) - entroy(后) 决策树:ID3 熵:表示随机变量的不确定性。变量不 确定性越高,熵越高