
§2.3静电场问题求解方法概述 直接积分法: 由电荷分布直接积分求场。 【例】 (p.34,例2-4):有一半径为a,面电荷密度为p 的均匀带电圆盘,求圆盘边缘上任一点的电位。 (解】:选观察点为坐标原点。 P,ds 4π60 R 源点 Ps RdRdo 4π6 R 2a cos0 dR πeo
§2.3 静电场问题求解方法概述 一、直接积分法: 由电荷分布直接积分求场。 R a 源点 场 点 x y 【例】(p. 34, 例 2-4):有一半径为 a,面电荷密度为 ρs 的均匀带电圆盘,求圆盘边缘上任一点的电位。 【解】:选观察点为坐标原点。 0 2 cos 0 / 2 / 2 0 0 0 4 4 4 1 a d dR R RdRd R dS s a s S s S s
§2.3静电场问题求解方法概述 二、高斯定理(十迭加原理 ①平板形电荷分布 【例】:无限大无限薄平板电荷分布。 分析可知:E=E脫 平板 由高斯定理可得: Ps x>0 260 X Ps x<0 260 对多个无限大无限薄平板,可应用迭加原理
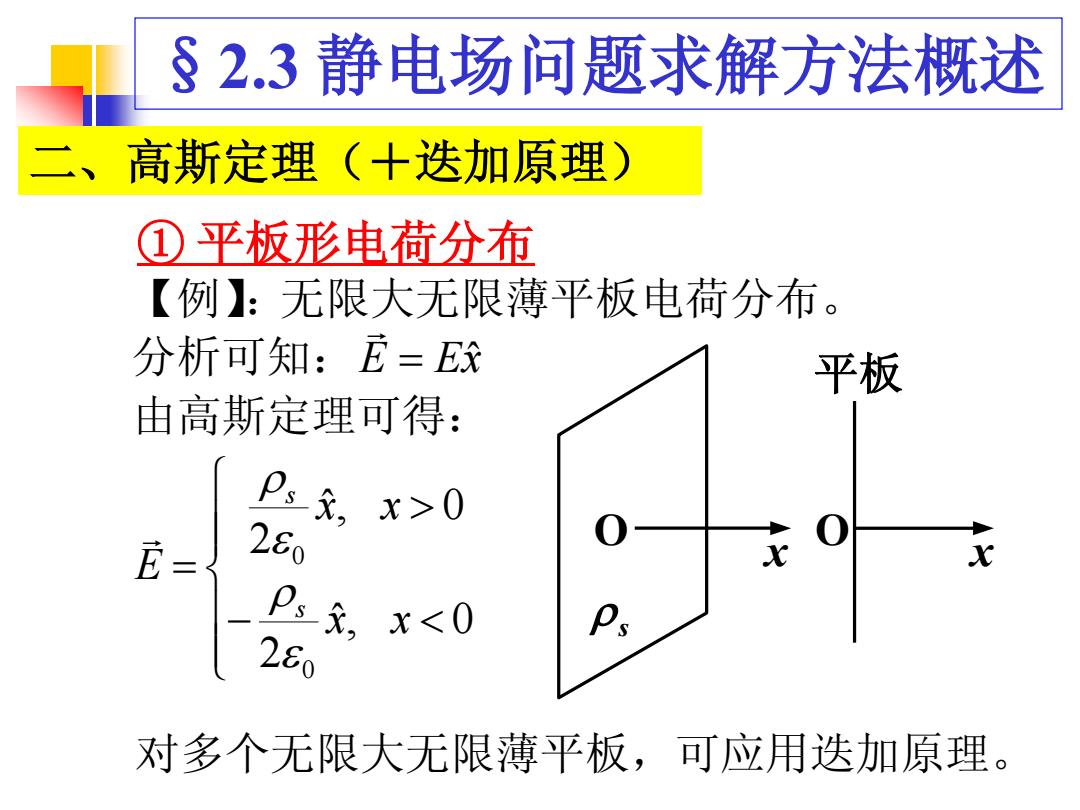
§2.3 静电场问题求解方法概述 二、高斯定理(+迭加原理) ① 平板形电荷分布 s x x O x x 平板 O 【例】:无限大无限薄平板电荷分布。 分析可知:E Exˆ 由高斯定理可得: ˆ, 0 2 ˆ, 0 2 0 0 x x x x E s s 对多个无限大无限薄平板,可应用迭加原理

【例】:体电荷密度为p(x)、厚度为d的 无限大平板电荷分布 E Ps。 3) 260 280 其中,p,=pxw。 X 08:=地 260 p(x) 区:=-必云wa 可见:(3)区和(1)区的场等同于面电荷密度为p的 无限大无限薄平板产生的场。在x→士∞的远 区更是如此。若p(x)反对称,则(3)区和(1) 区的场为零
(3)区: 0 0 2 2 s b a dx E 。 其中, b a s (x )dx 。 (1)区: 0 0 2 2 s b a dx E (2)区: b x x a b x x a dx dx dx dx E 0 0 0 2 1 2 2 【例】:体电荷密度为 ρ(x)、厚度为 d 的 无限大平板电荷分布 可见:(3)区和(1)区的场等同于面电荷密度为 ρs的 无限大无限薄平板产生的场。在x 的远 区更是如此。若 ρ(x)反对称,则(3)区和(1) 区的场为零。 b x ρ(x) (1) (2) (3) a

【例】(p.46,例2-5):p=P,求电 场强度和电位。 (3) E=E欧,ps=pod (3)区:E=P4 260 (1)☒:E=-PA 280 -d/2 d2 (2)区:E= x*-n爱小2 Po 选坐标原点为电位零点。等位面:=常数。 ②=o0-厂6f:-25= 260 3收:0=9+i-- Pod2 860 20 dx=- 280 880 0区:=同引--2h Pod 2o 880
(2)区: 0 2 0 0 0 0 0 2 ( ) ( ) (0) x dx x x x E d x x (3)区: 0 2 0 0 0 2 0 0 0 2 2 0 2 8 2 2 8 ( ) d x d dx d d E d d x x d d x (1)区: 0 2 0 0 2 0 0 0 0 2 2 0 2 8 2 8 ( ) d x d dx d d E d d x d x d x E Exˆ ,ρs=ρ0d (3)区: 0 0 2 d E 。 (1)区: 0 0 2 d E (2)区: 0 0 0 0 2 0 2 2 1 x x d d E x 选坐标原点为电位零点。等位面:x=常数。 d/2 x ρ0 (1) (2) (3) -d/2 O 【例】(p. 46, 例 2-5): 0,求电 场强度和电位

§2.3静电场问题求解方法概述 柱形电荷分布 =p()=p(x,y) 无限长线电荷分布p: E= 2π8r 无限长柱形体电荷分布p: S R d0' p=p(x,y) Ps 无限长柱形面电荷分布p: pdS→p.d',S→J
§2.3 静电场问题求解方法概述 ② 柱形电荷分布 (r) (x, y) 无限长线电荷分布 : r r E ˆ 2 0 无限长柱形体电荷分布 ρ: dS R r r R R E S , ˆ 2 1 0 无限长柱形面电荷分布 ρs: S dS sd , r dS (x, y) S s d ˆ z