
归东程子末军 5.1.2回溯法的基本思想 SHANDONG UNIVERSITY OF TECHNOLOGY 华器会空空合安会空会的会 ●在搜索至树中任一结,点时,先判断该结,点对应的部 分解是否满足约束条件,或者是否超出限界函数的 界,也就是判断该结点是否包含问题的(最优)解, 如果肯定不包含,则跳过对以该结,点为根的子树的 搜索,即所谓剪枝(Pruning);否则,进入以该结 点为根的子树,继续按照深度优先策略搜索。 ●在搜索过程中,通常采用两种策略避免无效搜索: ()用约束条件剪去得不到可行解的子树; (2)用限界函数剪去得不到最优解的子树。 这两类函数统称为剪枝函数(Pruning Function)。 2025年4月3日 21
2025年4月3日 21 5.1.2 回溯法的基本思想 ⚫ 在搜索至树中任一结点时,先判断该结点对应的部 分解是否满足约束条件,或者是否超出限界函数的 界,也就是判断该结点是否包含问题的(最优)解, 如果肯定不包含,则跳过对以该结点为根的子树的 搜索,即所谓剪枝(Pruning);否则,进入以该结 点为根的子树,继续按照深度优先策略搜索。 ⚫ 在搜索过程中,通常采用两种策略避免无效搜索: (1)用约束条件剪去得不到可行解的子树; (2)用限界函数剪去得不到最优解的子树。 这两类函数统称为剪枝函数(Pruning Function)
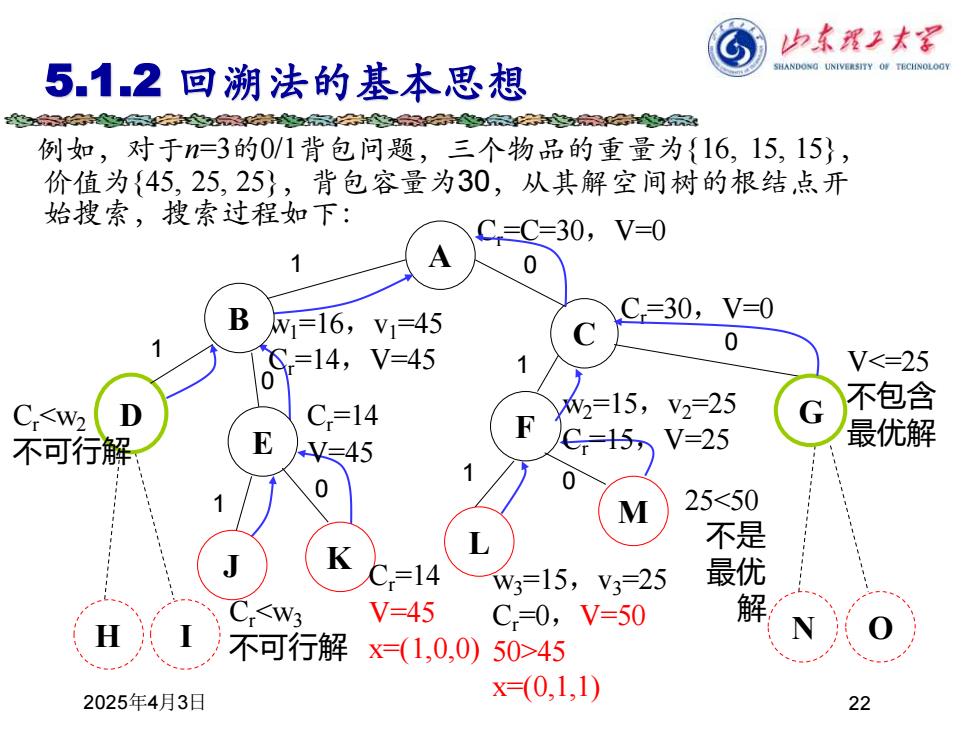
白东理上太黑 5.1.2回溯法的基本思想 SHANDONG UNIVERSITY OF TECHNOLOOY 华5空空实是子3分是,京☆ 例如,对于n=3的0/1背包问题,三个物品的重量为{16,15,15}, 价值为{45,25,25},背包容量为30,从其解空间树的根结,点开 始搜索,搜索过程如下: C=C=30,V=0 B w1=16,V1=45 C=30,V=0 014, 0 V=45 V<=25 Mw2=15,V2=25 不包含 C<w2 D C=14 不可行解 V=45 C=15 V=25 最优解 0 M 25<50 不是 C=14 w3=15,V3=25 最 <W3 V=45 C,=0,V=50 解 不可行解x=(1,0,0)50>45 2025年4月3日 x=(0,1,1) 22
2025年4月3日 22 5.1.2 回溯法的基本思想 例如,对于n=3的0/1背包问题,三个物品的重量为{16, 15, 15}, 价值为{45, 25, 25},背包容量为30,从其解空间树的根结点开 始搜索,搜索过程如下: A Cr=C=30,V=0 H I w1=16,v1=45 Cr=14,V=45 B 1 Cr<w2 D 不可行解 1 J Cr<w3 不可行解 1 F w2=15,v2=25 Cr=15,V=25 1 C Cr=30,V=0 0 Cr=14 E V=45 0 L w3=15,v3=25 Cr=0,V=50 50>45 x=(0,1,1) 1 K Cr=14 V=45 x=(1,0,0) 0 M 25<50 不是 最优 解 0 N O G V<=25 不包含 最优解 0

归东程子末军 5.1.2回溯法的基本思想 SHANDONG UNIVERSITY OF TECHNOLOGY 华器会空空合安会空会的会 回溯法是一种通用性解法,可以将回溯法看作是 带优化的穷举法。 回潮法的基本思想是在一棵含有问题全部可能解 的状态空间树上进行深度优先搜索,解为叶子结 点,搜索过程中,每到达一个结点时,则判断该 结点为根的子树是否含有问题的解,如果不含有 问题的解,则放弃对该子树的搜索,退回到上层 父结点,继续下一步深度优先搜索过程。 在回溯法中,并不是先构造出整棵状态空间树 再进行搜索,而是在搜索过程,逐步构造出状态 空间树,即边搜索,边构造; 2025年4月3日 23
2025年4月3日 23 5.1.2 回溯法的基本思想 ◼回溯法是一种通用性解法,可以将回溯法看作是 带优化的穷举法。 ◼回溯法的基本思想是在一棵含有问题全部可能解 的状态空间树上进行深度优先搜索,解为叶子结 点,搜索过程中,每到达一个结点时,则判断该 结点为根的子树是否含有问题的解,如果不含有 问题的解,则放弃对该子树的搜索,退回到上层 父结点,继续下一步深度优先搜索过程。 ◼在回溯法中,并不是先构造出整棵状态空间树, 再进行搜索,而是在搜索过程,逐步构造出状态 空间树,即边搜索,边构造;

白东程子太军 5.1.3递归回溯 SHANDONG UNIVERSITY OF TECINOLOGY 华绿修空点冷华会品品 void backtrack (int t) 表示递归深度,即对解空间树的第层节点进行深度优先搜索; if(t>n)output(;ln表示解空间树的高度; else for (int i=f(n,t);i<=g(n,t);i++){ /f(,t)和gn,t)分别表示在当前扩展结点处末搜索过的子树的起始 编号和终止编号; t)]=h(①);h)表示在当前扩展结点处t的第i个可选值; if(constraint(t)&&bound(t))backtrack(t+1); ∥constraint(t)和oound()分别表示在当前扩展结点处的约束函数 和限界函数; 2025年4月3日 24
2025年4月3日 24 5.1.3 递归回溯 void backtrack (int t) //t表示递归深度,即对解空间树的第t层节点进行深度优先搜索; { if (t>n) output(x); //n表示解空间树的高度; else for (int i=f(n,t);i<=g(n,t);i++) { //f(n,t)和g(n,t)分别表示在当前扩展结点处未搜索过的子树的起始 编号和终止编号; x[t]=h(i); //h(i)表示在当前扩展结点处x[t]的第i个可选值; if (constraint(t)&&bound(t)) backtrack(t+1); // constraint(t)和bound(t)分别表示在当前扩展结点处的约束函数 和限界函数; } }

归东理子太军程 5.1.4迭代回溯 SHANDONG UNIVERSITY OF TECHNOLOGY 华器会空空合安的会器空会的会路 void IterativeBacktrack ( { int t=1; while (t>0){ if (f(n,t)<=g(n,t)) for (int i=f(n,t);i<=g(n,t);i++) 对t]=h(0); if(constraint(t)&&bound(t)){ /函数solution()判断在当前扩展结点处是否找到问题的 一个可行解; if (solution(t))output(x); else t++;) } else t-; 2025年4月3日 25
2025年4月3日 25 5.1.4 迭代回溯 void IterativeBacktrack () { int t=1; while (t>0) { if (f(n,t)<=g(n,t)) for (int i=f(n,t);i<=g(n,t);i++) { x[t]=h(i); if (constraint(t)&&bound(t)) { //函数solution(t)判断在当前扩展结点处是否找到问题的 一个可行解; if (solution(t)) output(x); else t++;} } else t-; } }