
引言 归本程上太军 SHANDONG UNIVERSITY OF TECHNOLOGY ●有许多问题,当需要找出它的解集或者要求回答 什么解是满足某些约束条件的最佳解时,往往要 使用回溯法。 ● 回溯法的基本做法是搜索,或是一种组织得井井 有条的、能避免不必要搜索的穷举式搜索法。这 种方法适用于解一些组合数相当大的问题。 回溯法在问题的解空间树中,按深度优先策略, 从根结点出发搜索解空间树。算法搜索至解空间 树的任意一点时,先判断该结点是否包含问题的 解:如果肯定不包含,则跳过对该结点为根的子 树的搜索,逐层向其祖先结点回溯;否则,进入 该子树,继续按深度优先策略搜索。 2025年4月3日
2025年4月3日 11 引言 ⚫ 有许多问题,当需要找出它的解集或者要求回答 什么解是满足某些约束条件的最佳解时,往往要 使用回溯法。 ⚫ 回溯法的基本做法是搜索,或是一种组织得井井 有条的、能避免不必要搜索的穷举式搜索法。这 种方法适用于解一些组合数相当大的问题。 ⚫ 回溯法在问题的解空间树中,按深度优先策略, 从根结点出发搜索解空间树。算法搜索至解空间 树的任意一点时,先判断该结点是否包含问题的 解:如果肯定不包含,则跳过对该结点为根的子 树的搜索,逐层向其祖先结点回溯;否则,进入 该子树,继续按深度优先策略搜索

白东程子太军 5.1回溯法的算法框架 SHANDONG UNIVERSITY OF TECHNOLOOY 会会空的3会的是条 ●本节介绍回溯法算法框架的有关问题: ■一、问题的解空间 ■二、回溯法的基本思想 ■三、递归回溯 ■四、迭代回溯 ■五、子集树与排列树 2025年4月3日 12
2025年4月3日 12 5.1 回溯法的算法框架 ⚫ 本节介绍回溯法算法框架的有关问题: ◼一、问题的解空间 ◼二、回溯法的基本思想 ◼三、递归回溯 ◼四、迭代回溯 ◼五、子集树与排列树
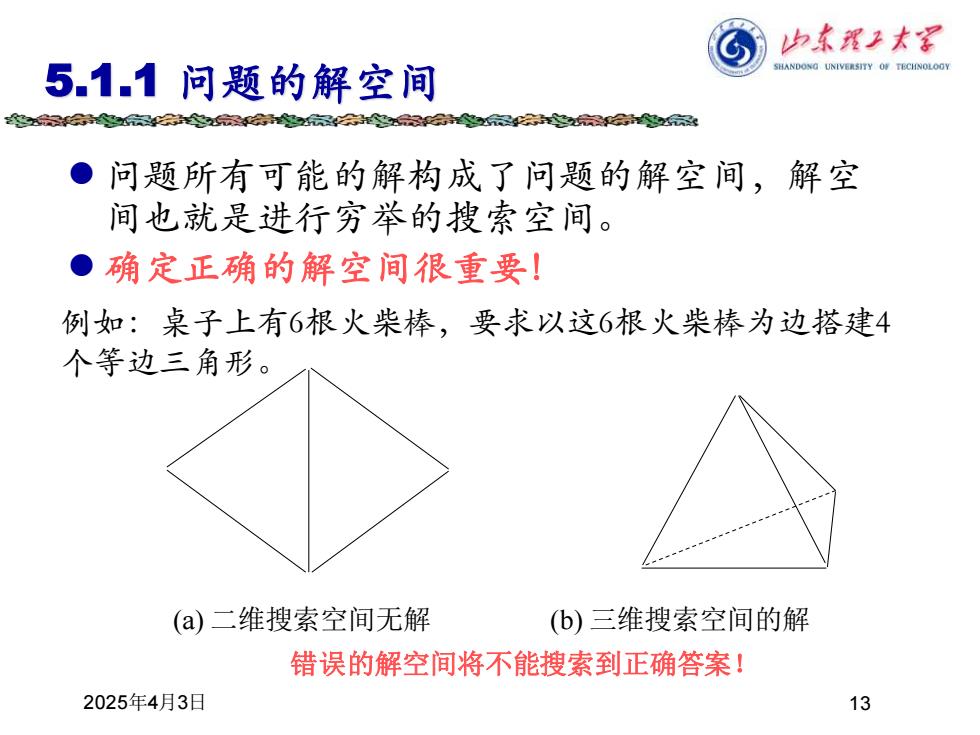
归本程子末军 5.1.1问题的解空间 SHANDONG UNIVERSITY OF TECHNOLOGY 红会合会点会器空深会是会点 ●问题所有可能的解构成了问题的解空间,解空 间也就是进行穷举的搜索空间。 ●确定正确的解空间很重要! 例如:桌子上有6根火柴棒,要求以这6根火柴棒为边搭建4 个等边三角形。 (a)二维搜索空间无解 (b)三维搜索空间的解 错误的解空间将不能搜索到正确答案! 2025年4月3日 13
2025年4月3日 13 5.1.1 问题的解空间 ⚫ 问题所有可能的解构成了问题的解空间,解空 间也就是进行穷举的搜索空间。 ⚫ 确定正确的解空间很重要! 例如:桌子上有6根火柴棒,要求以这6根火柴棒为边搭建4 个等边三角形。 (a) 二维搜索空间无解 (b) 三维搜索空间的解 错误的解空间将不能搜索到正确答案!

白东程子太军 5.1.1问题的解空间 HANDONG UNIVERSITY OF TECHNOLOOY 的合会3纹会品条 ●对于任何一个问题,可能解的表示方式和它相应的 解释隐含了解空间及其大小。 ●例如,对于有个物品的0/1背包问题,其可能解的 表示方式可以有以下两种: (1)可能解由一个不等长向量组成,当物品i(1≤≤n)装入 背包时,解向量中包含分量,否则,解向量中不包含分 量i,当=3时,其解空间是: {(),(1),(2),(3),(1,2),(1,3),(2,3),(1,2,3)} (2)可能解由一个等长向量{1,X2,Xm}组成,其中 X=1(1≤还n)表示物品i装入背包,x=0表示物品i没有装 入背包,当=3时,其解空间是: {(0,0,0),(0,0,1),(0,1,0),(1,0,0),(0,1,1),(1,0,1), (1,1,0),(1,1,1)} 2025年4月3日 14
2025年4月3日 14 5.1.1 问题的解空间 ⚫ 对于任何一个问题,可能解的表示方式和它相应的 解释隐含了解空间及其大小。 ⚫ 例如,对于有n个物品的0/1背包问题,其可能解的 表示方式可以有以下两种: (1)可能解由一个不等长向量组成,当物品i(1≤i≤n)装入 背包时,解向量中包含分量i,否则,解向量中不包含分 量i,当n=3时,其解空间是: { ( ), (1), (2), (3), (1, 2), (1, 3), (2, 3), (1, 2, 3) } (2)可能解由一个等长向量{x1 , x2 , ., xn }组成,其中 xi=1(1≤i≤n)表示物品i装入背包,xi=0表示物品i没有装 入背包,当n=3时,其解空间是: {(0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0), (1, 1, 1) }

归本程子末军 SHANDONG UNIVERSITY OF TECINOLOGY 器会会空会品器会的是会 •问题的解向量:回溯法希望一个问题的解能够表示 成一个n元式(x1,x2,.,xn)的形式。 ·显约束:对分量x的取值限定。 •隐约束:为满足问题的解而对不同分量之间施加的 约束。 •解空间:对于问题的一个实例,解向量满足显式约 束条件的所有多元组,构成了该实例的一个解空间。 注意:同一个问题可以有多种表示,有些 表示方法更简单,所需表示的状态空间更 小(存储量少,搜索方法简单)。 2025年4月3日 15
2025年4月3日 15 •问题的解向量:回溯法希望一个问题的解能够表示 成一个n元式(x1,x2,.,xn)的形式。 •显约束:对分量xi的取值限定。 •隐约束:为满足问题的解而对不同分量之间施加的 约束。 •解空间:对于问题的一个实例,解向量满足显式约 束条件的所有多元组,构成了该实例的一个解空间。 注意:同一个问题可以有多种表示,有些 表示方法更简单,所需表示的状态空间更 小(存储量少,搜索方法简单)