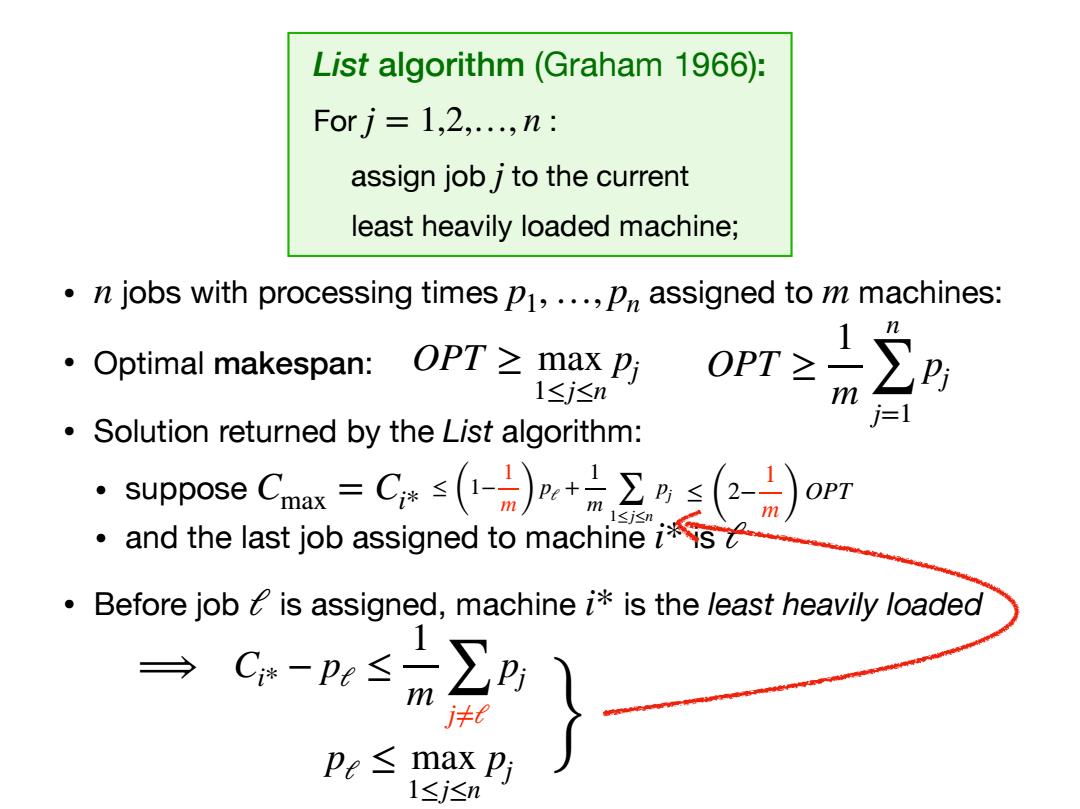
List algorithm (Graham 1966): Forj=1,2,.,n: assign job j to the current least heavily loaded machine; n jobs with processing times p1,...,p assigned to m machines: ·Optimal makespan:OPT≥max P; 1≤j≤n m i=1 Solution returned by the List algorithm: ·Suppose C=C≤(-H)+六三(月)oPr and the last job assigned to machine is Before job is assigned,machine i is the least heavily loaded 9C-w≤元∑4 Pe≤ max Pi 1≤j≤n
• jobs with processing times assigned to machines: • Optimal makespan: • Solution returned by the List algorithm: • suppose • and the last job assigned to machine is • Before job is assigned, machine is the least heavily loaded n p1,…, pn m Cmax = Ci* i* ℓ ℓ i* ⟹ Ci* − pℓ ≤ 1 m ∑ j≠ℓ pj List algorithm (Graham 1966): For : assign job to the current least heavily loaded machine; j = 1,2,…, n j OPT ≥ max 1≤j≤n pj OPT ≥ 1 m n ∑ j=1 pj pℓ ≤ max 1≤j≤n pj } ≤ (1− 1 m) pℓ + 1 m ∑ 1≤j≤n pj ≤ (2− 1 m) OPT

Graham's List Algorithm List algorithm (Graham 1966): Forj=1,2,.,n: assign job j to the current least heavily loaded machine; n jobs are assigned to m machines The List algorithm returns a schedule with makespan: .Caw≤(k-)opr This is tight in the worst case
Graham’s List Algorithm List algorithm (Graham 1966): For : assign job to the current least heavily loaded machine; j = 1,2,…, n j • jobs are assigned to machines • The List algorithm returns a schedule with makespan: • • This is tight in the worst case. n m Cmax ≤ (2 − 1 m) OPT

Local Search locally improve the solution until no improvement can be made (local optima,fixpoint) Local search: Start from an arbitrary schedule; repeat until no job is reassigned (a local optima): if the last finished job can finish earlier by moving to machine i transfer job&to machine i;
Local Search locally improve the solution until no improvement can be made (local optima, fixpoint) Local search: Start from an arbitrary schedule; repeat until no job is reassigned (a local optima): if the last finished job can finish earlier by moving to machine transfer job to machine ; ℓ i ℓ i

Local search: Start from an arbitrary schedule; repeat until no job is reassigned(a local optima): if the last finished job&can finish earlier by moving to machine i transfer job to machine i; 。Optimal makespan:OPT≥】 max Pi OPT≥1∑B 1≤j≤n m ·In a local optima: 1≤j≤n ·pC=C)+8(e-)or and job finishes the last ·local optima→Ci*-P is the least heavy load C-P%s∑n m Pe≤ max Pi 1≤jsn
Local search: Start from an arbitrary schedule; repeat until no job is reassigned (a local optima): if the last finished job can finish earlier by moving to machine transfer job to machine ; ℓ i ℓ i • Optimal makespan: • In a local optima: • suppose • and job finishes the last • local optima is the least heavy load Cmax = Ci* ℓ ⟹Ci* − pℓ OPT ≥ max 1≤j≤n pj OPT ≥ 1 m ∑ 1≤j≤n pj Ci* − pℓ ≤ 1 m ∑ j≠ℓ pj pℓ ≤ max 1≤j≤n pj ≤ (1− 1 m ) pℓ + 1 m ∑ 1≤j≤n pj ≤ (2− 1 m ) OPT }

Local search: Start from an arbitrary schedule; repeat until no job is reassigned(a local optima): if the last finished job&can finish earlier by moving to machine i transfer job to machine i; For a local optima: List algorithm(Graham 1966): the schedule returned Forj=1,2,.,n: by the List algorithm assign job j to the current must be a local optima least heavily loaded machine; 。→ the schedule returned by the List algorithm: cns≤(2-)or
Local search: Start from an arbitrary schedule; repeat until no job is reassigned (a local optima): if the last finished job can finish earlier by moving to machine transfer job to machine ; ℓ i ℓ i For a local optima: Cmax ≤ (2− 1 m) OPT List algorithm (Graham 1966): For : assign job to the current least heavily loaded machine; j = 1,2,…, n j the schedule returned by the List algorithm must be a local optima • ⟹ the schedule returned by the List algorithm: Cmax ≤ (2− 1 m) OPT