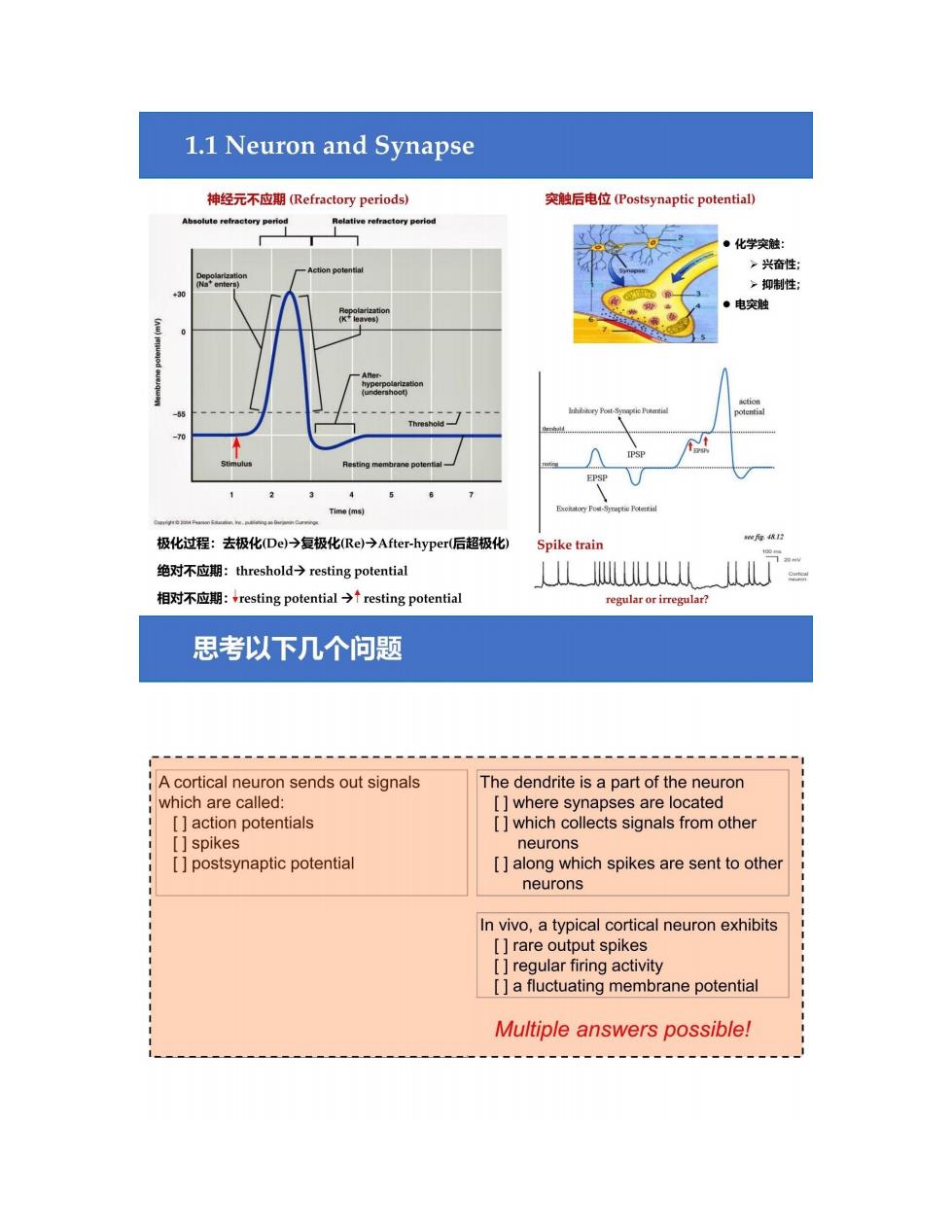
1.1 Neuron and Synapse 神经元不应期(Refractory periods) 突触后电位(Postsynaptic potential) Absolute refractory period Rolative refractory period ●化学突触: >兴奋性: >抑制性: 30 ·电突触 action Post-S oEat EPSP 2 3 4 5 Tme(ms Exitatory Po-Syeptic Poteial 极化过程:去极化(De)→复极化(Re)→After-hyper(后超极化) Spike train 绝对不应期:threshold→resting potential 相对不应期:resting potential→resting potential regular or irregular? 思考以下几个问题 A cortical neuron sends out signals The dendrite is a part of the neuron which are called: where synapses are located [action potentials which collects signals from other [spikes neurons [postsynaptic potential [along which spikes are sent to other neurons In vivo,a typical cortical neuron exhibits rare output spikes [regular firing activity [a fluctuating membrane potential Multiple answers possible!

How to model neurons:A simple way 整合发放(integrate-and-fire)思想 Spike Spike reception emission 一一一 9 linearly >Spikes are events >triggered at threshold Urest ↑↑↑↑1 spike/reset/refractoriness t Subthreshold regime 1.2 The Passive Membrane 考虑采用RC电路来模拟被动膜 () I(t). E 膜电位:=4n~out 22 膜外 膜内 dt u-E)+IE=re R du 不考虑压控离子通道 =-(u-E)+RI dt

1.2 The Passive Membrane 考虑第1种情况: I() 若初始条件满足u(O)=4st+u和()=0,试分析u随时间的变化 R 数学分析过程: 令V=u-urest 则业 d(u-ure)_-V+Rl dt dt T 因为It)=0,所以:V=Cer=u-ue d=-(u-we)+R d 考虑初始条件u(0)=uet+lo,可得到:C=4o 1u↑ 解为:u=4e+uer 以指数形式达到稳态4est >膜时间常数控制达稳态速度 1.2 The Passive Membrane (step response) 考虑第2种情况(step current input): I(t)为下图所示的阶跃函数,初始条件满足u(t)=4est(t冬t), I(t) 试分析u随时间的变化 以指数相关的形式达到稳态lest+R R 达到稳态后所有电流都从电阻走 =-(u-uet)+Rl dt w+I-Ce学→C=-,→u=w+M,a-e台)

1.2 The Passive Membrane (impulse response) 考虑第3种情况: I(t)为下图所示的脉冲电流,始条件满足u()=4est(t≤t6), I(t) 试分析u随时间的变化 △=t1-t 以指数相关的形式达到一个值后, R 再以指数形式下降至4,est u rest d=-(u-une)+Rl d _1-a u(t)=urest +IoR(1-e ),to<tst 1-1 u(t)=ures +[u(t)-ures Je :,t>t 1.2 The Passive Membrane (impulse response) 基于第3种情况,考虑更特殊的情况△趋于零时,随时间的变化 快速到达4res+Io△/C后,指数衰减 I(t) u rest to t - △ =-(u-4et)+Rl u=ures +Rlo(l-e :)=ures +RIo(l-e : x2x3 狄拉克δ函数 由于e'=1+x+ +…(Taylor展开) 23! δ(t)=0,t≠0 得到u=uew+RL, T 6()d=1
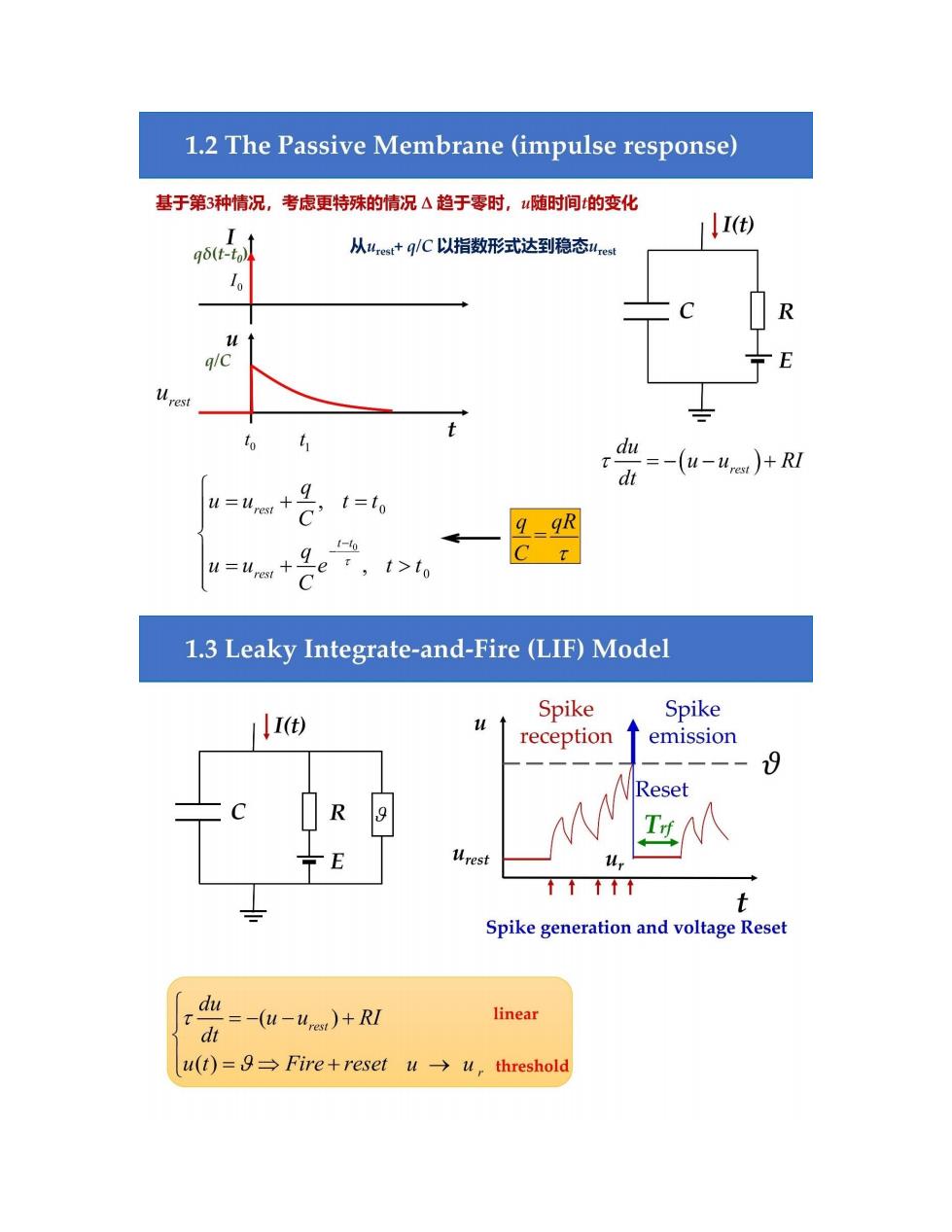
1.2 The Passive Membrane (impulse response) 基于第3种情况,考虑更特殊的情况△趋于零时,随时间的变化 I(t) gδ(t-to 从4,et+q/C以指数形式达到稳态lret R q/c ÷E Uresi to t d=-(u-)+Rl d u=+名1= e r,t>to C 1.3 Leaky Integrate-and-Fire (LIF)Model I() Spike Spike reception emission 8 Reset R urest ↑↑↑↑1 t Spike generation and voltage Reset du T linear dt =-(u-urest)+RI u(t)=g→Fire+reset u→u,threshold