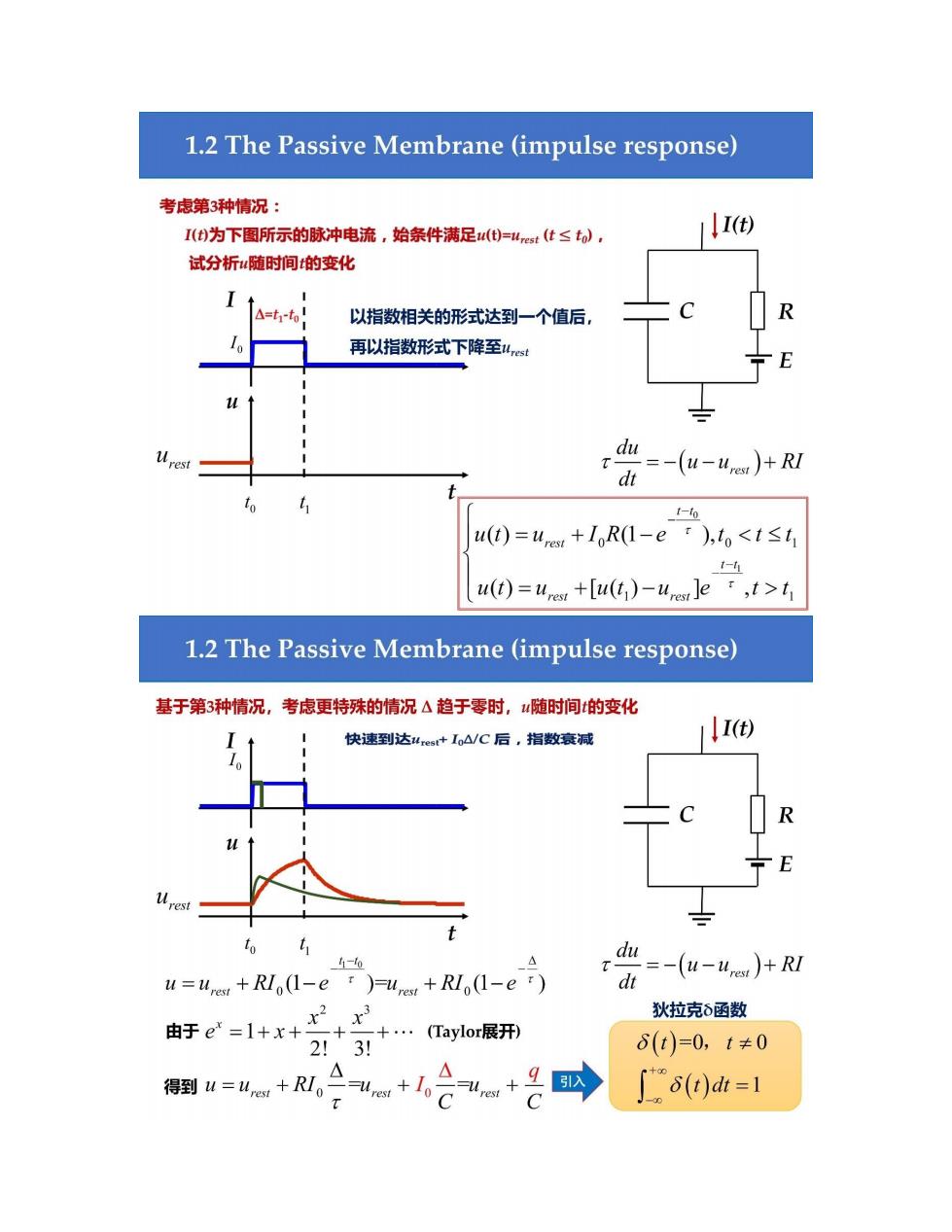
1.2 The Passive Membrane (impulse response) 考虑第3种情况: I(t)为下图所示的脉冲电流,始条件满足u()=4est(t≤t6), I(t) 试分析u随时间的变化 △=t1-t 以指数相关的形式达到一个值后, R 再以指数形式下降至4,est u rest d=-(u-une)+Rl d _1-a u(t)=urest +IoR(1-e ),to<tst 1-1 u(t)=ures +[u(t)-ures Je :,t>t 1.2 The Passive Membrane (impulse response) 基于第3种情况,考虑更特殊的情况△趋于零时,随时间的变化 快速到达4res+Io△/C后,指数衰减 I(t) u rest to t - △ =-(u-4et)+Rl u=ures +Rlo(l-e :)=ures +RIo(l-e : x2x3 狄拉克δ函数 由于e'=1+x+ +…(Taylor展开) 23! δ(t)=0,t≠0 得到u=uew+RL, T 6()d=1
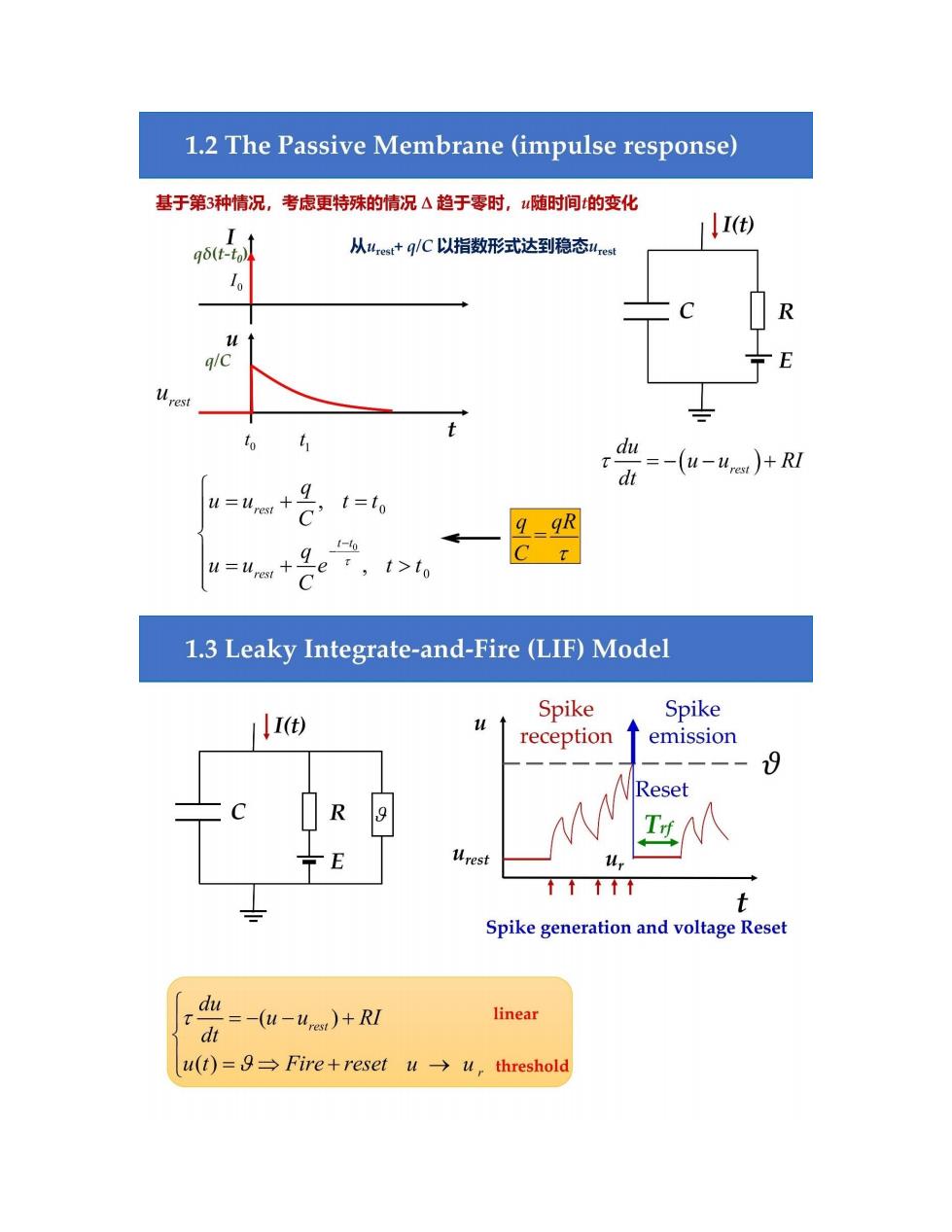
1.2 The Passive Membrane (impulse response) 基于第3种情况,考虑更特殊的情况△趋于零时,随时间的变化 I(t) gδ(t-to 从4,et+q/C以指数形式达到稳态lret R q/c ÷E Uresi to t d=-(u-)+R d u=+名1= e r,t>to C 1.3 Leaky Integrate-and-Fire (LIF)Model I() Spike Spike reception emission 8 Reset R urest ↑↑↑↑1 t Spike generation and voltage Reset du T linear dt =-(u-urest)+RI u(t)=g→Fire+reset u→u,threshold

1.3 Leaky Integrate-and-Fire Model 作业:当D,≠D,es时,求LF神经 我们考虑一个简单的形式,即当:,=0es时, 元放电率公式(解析解和数值解) 若F神经元接收常电流,那么膜电位从静息电位开始需要多久放电? 1-to a 1=1.8μA 令u=ue+RL(l-et))=9 至201 0 1=202μA 毫20 21A 220 40 60 RIo r (ms) RIo-9+urest du linear T+Td dt =-(u-4e)+RI u(t)=9→Fire+reset u-→u,threshold Io= 9-urest R 1.3 Leaky Integrate-and-Fire Model 怎样利用计算机做数值解:欧拉法、改进欧拉法、龙格库塔法等等 dy 欧拉法精度O(h) 考虑如下微分方程和初始值条件: =f(x,y) and dx y(xo)=Yo 可用欧拉法计算其数值解: (x4y4) x1=x+△x ○ (x1,y)= =y+f(xo,yo)△x (x33)。 (1y1) (Xacyact) x2=x1+△x (x2,2)= (2y2) y2=y+f(x,y)△ (xoyo) △x x3=x2+△x (x3,3)= 3=2+f(x2,y2)△x X0 X1 X2 X3 X4 x4=x3+△x xn+=xn+△x (x4,y4)= (X)= y4=y3+f(x3,3)△x yn1=yn+f(xn,yn)△x
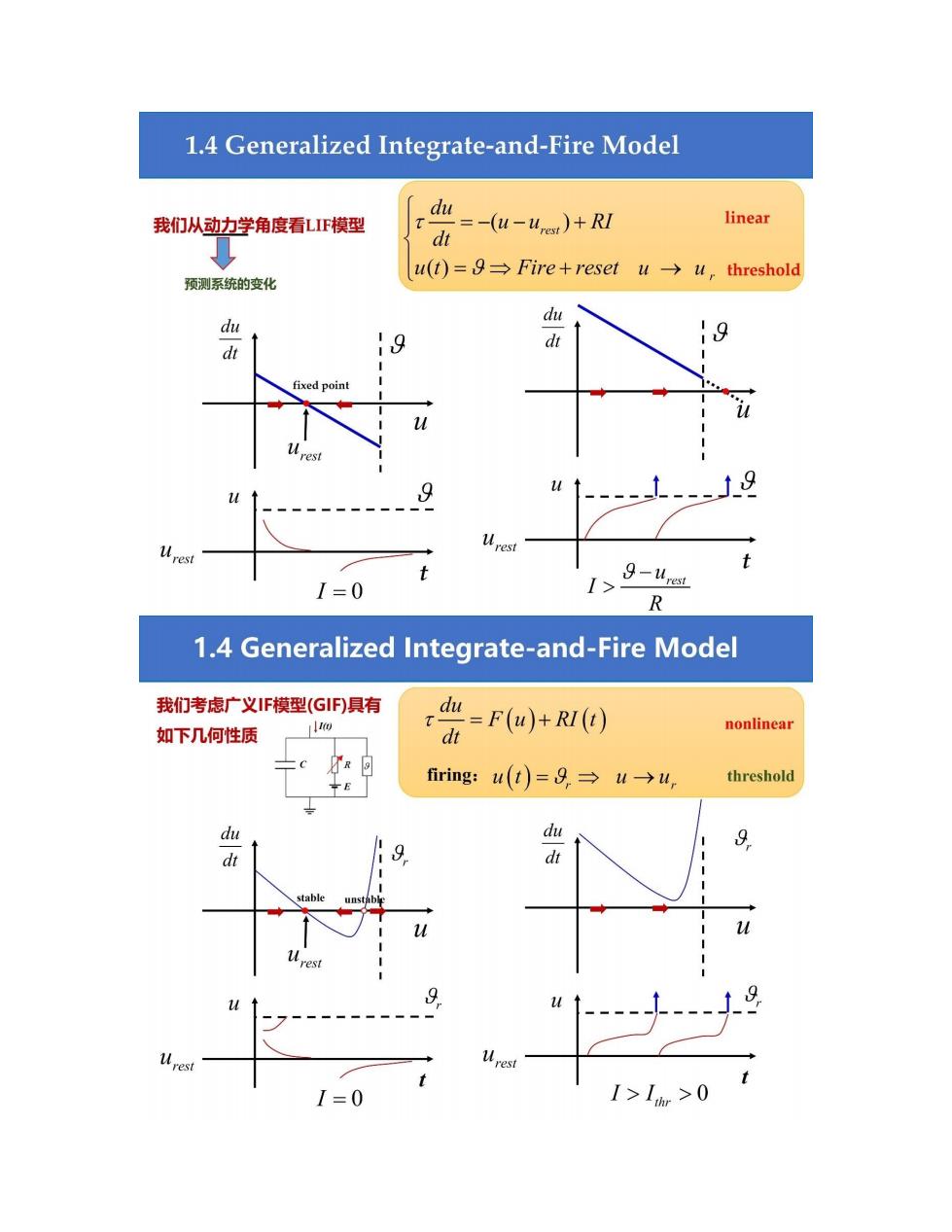
1.4 Generalized Integrate-and-Fire Model du 我们从动力学角度看LIF模型 =-(u-urest)+RI linear ↓ dt u(t)=9→Fire+reset u-u,threshold 预测系统的变化 du du dt 19 fixed point Urest I> g-urest R 1.4 Generalized Integrate-and-Fire Model 我们考虑广义F模型(GF)具有 1 rdu-F(u)+RI(t) dt nonlinear 如下几何性质 firing:u(t))=9,→u>u, threshold du du 9, dt 9 stable rest I0
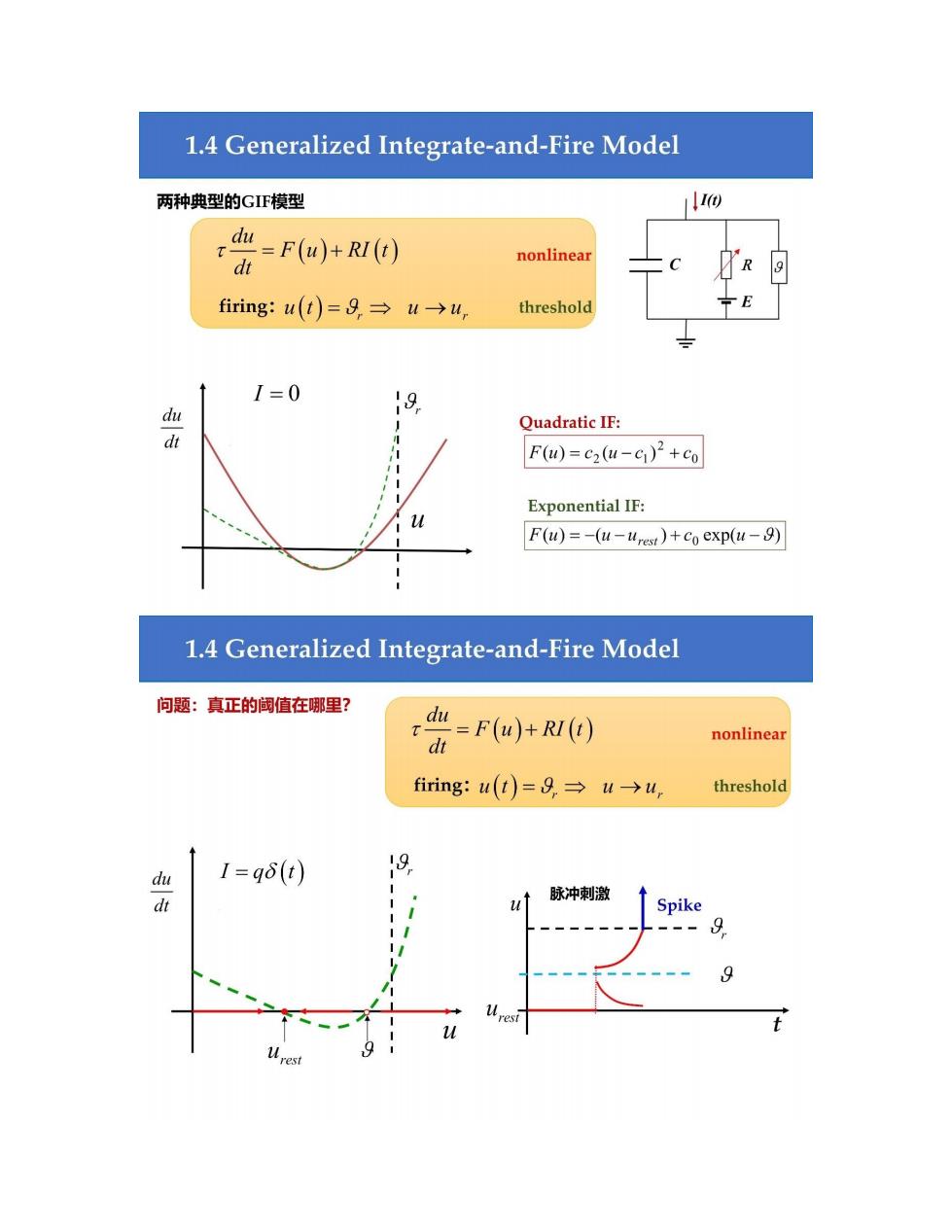
1.4 Generalized Integrate-and-Fire Model 两种典型的GF模型 du dt =F(u)+RI(t) nonlinear firing:u(t))=9,→u→w, threshold I=0 19 Quadratic IF: F(u)=c2(u-c1)2+co Exponential IF: F(u)=-(u-urest)+co exp(u-9) 1.4 Generalized Integrate-and-Fire Model 问题:真正的阈值在哪里? d=F(u)+RI() nonlinear firing:u(t)=9,→u→w, threshold 1=qδ(t) 9 脉冲刺激 Spike 9 u resi rest