
China-pub.com 第4章自顶向下的分析 115 下载 现在A之后的记号,则要挑选A一α以使A消失。请注意规则2中当=E时的特殊情况。 很难直接完成这些规则。在下一节中,我们将为此开发一个算法,这其中包括了早已提到 过的Fist和FoIlow集合。但在极为简单的例子中,这些规则是可手工完成的。 读者可考虑在前一小节中使用成对括号的文法的第1个示例,它有一个非终结符(S、3个 记号(左括号、右括号和$),以及两个选择。由于5只有一个非空产生式,即S一(S,每 个可从S派生的串必须或为空或以左括号开始,并将这个产生式选择添加到项目M[S,中(且 仅能在这里)。这样就完成了规则1之下的所有情况。因为有S一(S)S,规则2应用了α=e, =(,A=S,a=)且y=S$,所以S→e就被添加到MS,)】中了。由于SS一*S$(空推导), 所以S一e也被添加到MS,S】中。这样就完成了这个文法的LL()分析表的构造,我们可以将 它写在下面的格式中: MIN.T] $ S→(5)5 S→6S→e 为了完善LL(1)分析算法,该表必须为每个非终结符-记号对给出唯一选择,可以从下面的 定义开始。 定义:如果文法G相关的LL(1)分析表的每个项目中至多只有一个产生式,则该文法 就是LL(1)文法(LL(l)grammar)。 由于上面的定义暗示着利用LL(I)文法表就能构造出一个无二义性的分析,所以LL(1)文法 不能是二义性的。当给出LL(1)文法时,程序清单4-2中有使用LL(1)分析表的一个分析算法。 这个算法完全导致了在前一小节的示例中描述的那些动作。 虽然程序清单4-2中的算法要求分析表的每个项目最多只能有一个产生式,但仍有可能在 表构造中建立消除二义性的规则,它可处理简单的二义性情况,如在与递归下降程序相似的方 式中的悬挂clse问题。 程序清单42基于表的LL(1)分析算法 of the parsing s the mext input token◆sdo then (match" push X onto the parsing stack; tppma- the next input token =S then ac else error;
现在A之后的记号,则要挑选A→a以使A消失。请注意规则2中当a= 时的特殊情况。 很难直接完成这些规则。在下一节中,我们将为此开发一个算法,这其中包括了早已提到 过的F i r s t和F o l l o w集合。但在极为简单的例子中,这些规则是可手工完成的。 读者可考虑在前一小节中使用成对括号的文法的第 1个示例,它有一个非终结符 (S)、3个 记号(左括号、右括号和 $),以及两个选择。由于 S只有一个非空产生式,即 S→(S)S,每一 个可从S派生的串必须或为空或以左括号开始,并将这个产生式选择添加到项目 M [S, (] 中(且 仅能在这里)。这样就完成了规则 1之下的所有情况。因为有 S Þ (S) S,规则2应用了a= , b= (, A = S, a = ) 且g = S $,所以S→ 就被添加到M [S, )] 中了。由于S $ Þ *S$(空推导), 所以S→ 也被添加到M [S, $] 中。这样就完成了这个文法的 L L ( 1 )分析表的构造,我们可以将 它写在下面的格式中: 为了完善L L ( 1 )分析算法,该表必须为每个非终结符 -记号对给出唯一选择,可以从下面的 定义开始。 定义:如果文法G相关的L L ( 1 )分析表的每个项目中至多只有一个产生式,则该文法 就是L L ( 1 )文法(LL(1) grammar)。 由于上面的定义暗示着利用L L ( 1 )文法表就能构造出一个无二义性的分析,所以 L L ( 1 )文法 不能是二义性的。当给出 L L ( 1 )文法时,程序清单 4 - 2中有使用L L ( 1 )分析表的一个分析算法。 这个算法完全导致了在前一小节的示例中描述的那些动作。 虽然程序清单4 - 2中的算法要求分析表的每个项目最多只能有一个产生式,但仍有可能在 表构造中建立消除二义性的规则,它可处理简单的二义性情况,如在与递归下降程序相似的方 式中的悬挂e l s e问题。 程序清单4-2 基于表的L L ( 1 )分析算法 第 4章 自顶向下的分析 1 1 5 下载
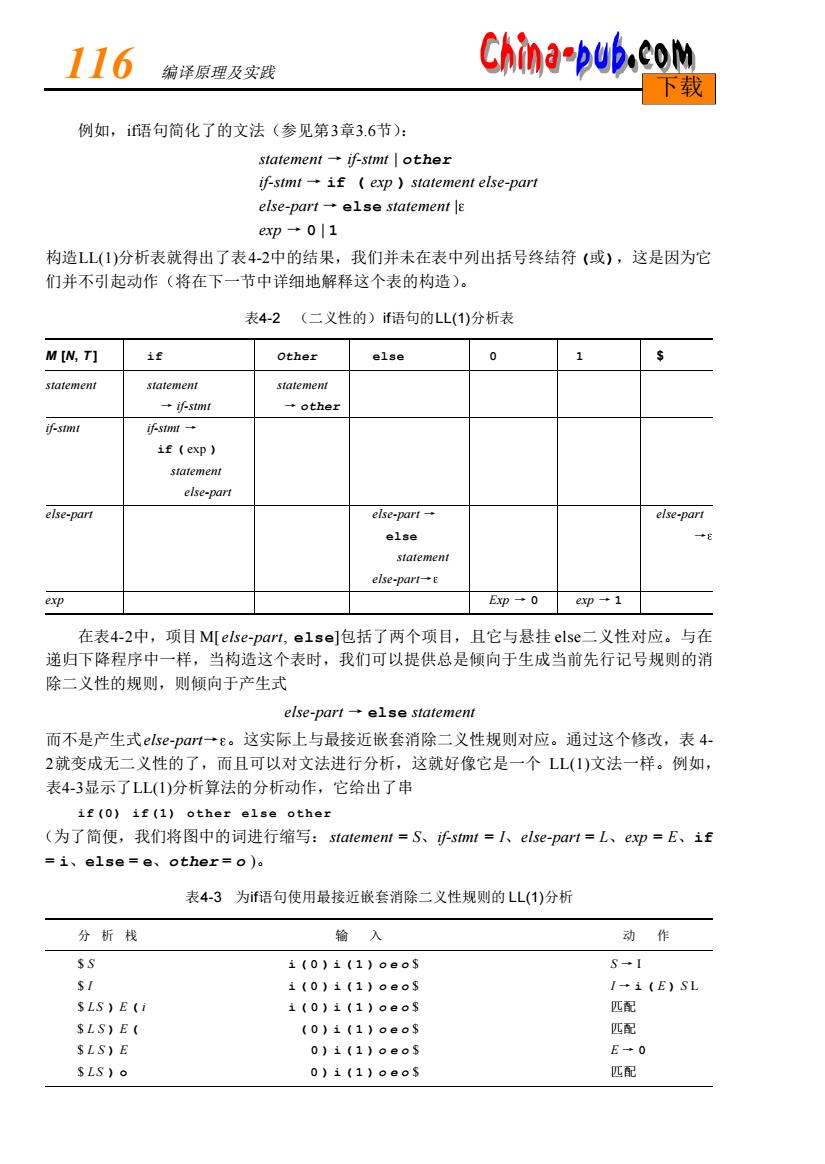
116 编译原理及实践 China-pub.co 下载 例如,i语句简化了的文法(参见第3章3.6节) statement-if-simt other if-stmt-if exp statement else-part else-part-else statement le ep→01 构造LL(1)分析表就得出了表4-2中的结果,我们并未在表中列出括号终结符(或),这是因为它 们并不引起动作(将在下一节中详细地解释这个表的构造)。 表4-2(二义性的)语句的LL(1)分析表 M IN,T] Other else 0 1 statement statement statement +ismt othe 小stm f (exp) statement else-part else-part else-pa→ else-part statemen ele-paH→E exp Exp0 exp-1 在表4-2中,项目M[else--pat,else]包括了两个项目,且它与悬挂else二义性对应。与在 递归下降程序中一样,当构造这个表时,我们可以提供总是倾向于生成当前先行记号规则的消 除二义性的规则,则倾向于产生式 else-part-else statement 而不是产生式ese-pam一e。这实际上与最接近嵌套消除二义性规则对应。通过这个修改,表4 2就变成无二义性的了,而且可以对文法进行分析,这就好像它是一个LL(1)文法一样。例如, 表4-3显示了LL()分析算法的分析动作,它给出了串 if(0)if(1)other else other (为了简便,我们将图中的词进行缩写:statement=S、诉sml=人、else-par1=L、exp=E、iE =i、else=e、other=0) 表4-3为f语句使用最接近嵌套消除二义性规则的LL(1)分析 分析栈 输入 动作 i(0)i(1)oeos S-1 i(0)i(1)oeoS I-(E)SL $LS)E(i i(0)i(1)oeoS 匹配 SLS)EU (0)i(1)oeoS 匹配 SLS)E 0)1(1)00s E0 0)(1)0os 匹配
例如,i f语句简化了的文法(参见第3章3 . 6节): statement → if-stmt | o t h e r if-stmt → if ( exp ) statement else-part e l s e - p a rt → e l s e statement | exp → 0 | 1 构造L L ( 1 )分析表就得出了表4 - 2中的结果,我们并未在表中列出括号终结符 (或),这是因为它 们并不引起动作(将在下一节中详细地解释这个表的构造)。 表4-2 (二义性的)i f语句的L L ( 1 )分析表 M [N, T ] i f O t h e r e l s e 0 1 $ s t a t e m e n t s t a t e m e n t s t a t e m e n t → i f - s t m t → o t h e r i f - s t m t if-stmt → i f ( exp ) s t a t e m e n t e l s e - p a rt e l s e - p a rt e l s e - p a rt → e l s e - p a rt e l s e → s t a t e m e n t e l s e - p a rt→ e x p Exp → 0 exp → 1 在表4 - 2中,项目M[ e l s e - p a rt, e l s e]包括了两个项目,且它与悬挂 e l s e二义性对应。与在 递归下降程序中一样,当构造这个表时,我们可以提供总是倾向于生成当前先行记号规则的消 除二义性的规则,则倾向于产生式 e l s e - p a rt → e l s e s t a t e m e n t 而不是产生式e l s e - p a rt→ 。这实际上与最接近嵌套消除二义性规则对应。通过这个修改,表 4 - 2就变成无二义性的了,而且可以对文法进行分析,这就好像它是一个 L L ( 1 )文法一样。例如, 表4 - 3显示了L L ( 1 )分析算法的分析动作,它给出了串 if(0) if(1) other else other (为了简便,我们将图中的词进行缩写:statement = S、if-stmt = I、e l s e - p a rt = L、exp = E、i f = i、e l s e = e、o t h e r = o )。 表4-3 为i f语句使用最接近嵌套消除二义性规则的 L L ( 1 )分析 分 析 栈 输 入 动 作 $ S i ( 0 ) i ( 1 ) o e o $ S → I $ I i ( 0 ) i ( 1 ) o e o $ I → i ( E ) S L $ L S ) E ( i i ( 0 ) i ( 1 ) o e o $ 匹配 $ L S ) E ( ( 0 ) i ( 1 ) o e o $ 匹配 $ L S ) E 0 ) i ( 1 ) o e o $ E → 0 $ L S ) o 0 ) i ( 1 ) o e o $ 匹配 1 1 6 编译原理及实践 下载

China-pub.com 第4章自顶向下的分析 117 下载 (续) 分析栈 输入 动作 SLS) )1(1)o9os 匹配 发Ls 1t1}。eas 餐+ SLI 4(1)00os SLLS)E 1-1(E)SL S LL S E (i 1(1)0903 配 S LL S E (1)oe05 匹配 S LL S)E 1)0e0s E+1 SLLS) 匹配 SILS 060S S LL e03 L-es SLS e eoS 匹配 $L5 oS S+0 $L0 os 匹配 4.2.3消除左递归和提取左因子 LL()分析中的重复和选择也存在着与在递归下降程序分析中遇到的类似问题,而且正是 由于这个原因,还不能够为前一节的简单算法表达式文法给出一个LL(1)分析表。我们利用 EBNF表示法解决了递归下降程序中的这些问题,但却不能在LL(I)分析中使用相同的办法:而 必须将BNF表示法中的文法重写到LL(I)分析算法所能接受的格式上。此时应用的两个标准技 术是左递归消除(left recursion removal)和提取左因子(left factoring)。我们将逐个考虑它们。 必须指出的是:这两个技术无法保证可将一个文法变成LL(I)文法,这就同EBNF一样无法保证 在编写递归下降程序中可以解决所有的问题。然而,在绝大多数情况下,它们都十分有用,并 且具有可自动操作其应用程序的优点,因此,假设有一个成功的结果,利用它们就可自动地生 成LL(1)分析程序(参见“注意与参考”一节)。 )左递归消除左递归被普遍地用来运算左结合,如在简单表达式文法中, exp-exp addop term term 使得运算由addop左结合来代表。这是左递归的最简单情况,在其中只有一个左递归产生式选 择。当有不止一个的选择是左递归时,就略微复杂一些了,如可将addop?写出来: exp-exp+term l exp-term term 这两种情况都涉及到了直接左递归(immediate left recursion),而左递归仅发生在一单个非终 结符(如exp)的产生式中。间接左递归是更复杂的情况,如在规则 A→Bb B→Aal. 中。这样的规则在真正的程序设计语言文法中几乎不可能发生,但本书为了完整仍给出它的解 决方法。首先考虑直接左递归
(续) 分 析 栈 输 入 动 作 $ L S ) ) i ( 1 ) o e o $ 匹配 $ L S i ( 1 ) o e o $ S → I $ L I i ( 1 ) o e o $ I → i ( E ) S L $ L L S ) E ( i i ( 1 ) o e o $ I → i ( E ) S L $ L L S ) E ( i i ( 1 ) o e o $ 匹配 $ L L S ) E ( ( 1 ) o e o $ 匹配 $ L L S ) E 1 ) o e o $ E → 1 $ L L S ) ) o e o $ 匹配 $ L L S o e o $ S → o $ L L o o e o $ 匹配 $ L L e o $ L → e S $ L S e e o $ 匹配 $ L S o $ S → o $ L o o $ 匹配 $ L $ L → $ $ 接受 4.2.3 消除左递归和提取左因子 L L ( 1 )分析中的重复和选择也存在着与在递归下降程序分析中遇到的类似问题,而且正是 由于这个原因,还不能够为前一节的简单算法表达式文法给出一个 L L ( 1 )分析表。我们利用 E B N F表示法解决了递归下降程序中的这些问题,但却不能在 L L ( 1 )分析中使用相同的办法;而 必须将B N F表示法中的文法重写到 L L ( 1 )分析算法所能接受的格式上。此时应用的两个标准技 术是左递归消除(left recursion removal)和提取左因子(left factoring)。我们将逐个考虑它们。 必须指出的是:这两个技术无法保证可将一个文法变成 L L ( 1 )文法,这就同E B N F一样无法保证 在编写递归下降程序中可以解决所有的问题。然而,在绝大多数情况下,它们都十分有用,并 且具有可自动操作其应用程序的优点,因此,假设有一个成功的结果,利用它们就可自动地生 成L L ( 1 )分析程序(参见“注意与参考”一节)。 1) 左递归消除 左递归被普遍地用来运算左结合,如在简单表达式文法中, exp → exp addop term | t e r m 使得运算由a d d o p左结合来代表。这是左递归的最简单情况,在其中只有一个左递归产生式选 择。当有不止一个的选择是左递归时,就略微复杂一些了,如可将 a d d o p写出来: exp → exp + term | exp - term | t e r m 这两种情况都涉及到了直接左递归( immediate left recursion),而左递归仅发生在一单个非终 结符(如e x p)的产生式中。间接左递归是更复杂的情况,如在规则 A → B b | . . . B → A a | . . . 中。这样的规则在真正的程序设计语言文法中几乎不可能发生,但本书为了完整仍给出它的解 决方法。首先考虑直接左递归。 第 4章 自顶向下的分析 1 1 7 下载

118 编译原理及实践 China-pub.co 下载 情况1:简单直接左递归 在这种情况下,左递归只出现在格式 A-AaIB 的文法规则中,其中α和B是终结符和非终结符的串,而且B不以4开头。在3.2.3节中,我们看 到这个文法规则生成了格式Ba(n≥0)的串。选择A一B是基本情况,而A一Aa是递归情况。 为了消除左递归,将这个文法规则重写为两个规则:一个是首先生成B,另一个是生成的 重复,它不用左递归却用右递归: A一B A'→a'|e 例4.1再次考虑在简单表达式文法中的左递归规则: exp-exp addop term term 它属于格式A一AaB,且A=exp,a=addop1em,B=erm。将这个规则重写以消除左递归, 就可得到 exp→term exp' exp'-addop term exp'le 情况2:普遍的直接左递归 这种情况发生在有如下格式的产生式 4-Ma,1 4a,1...14a,I B,IB,1...IB. 中。其中B,…,阝,均不以4开头。在这种情况下,其解法与简单情况类似,只需将选择相应地 扩展: A→B.A'IB.A'1..1BA" 例4.2考虑文法规则 exp exp term exp -term term 如下消除左递归: ep→term exp exp'-+term exp'-term exp' 情况3:一般的左递归 这里描述的算法仅是指不带有e产生式且不带有循环的文法,其中循环(cyce)是至少有 一步是以相同的非终结符:A三α三*A开始和结束的推导。循环几乎背定能导致分析程序进入 无穷循环,而且带有循环的文法从不作为程序设计语言文法出现。程序设计语言文法确实是有 ε产生式,但这经常是在非常有限的格式中,所以这个算法对于这些文法也几乎总是有效的。 该算法的方法是:为语言的所有非终结符选择任意顺序,如A, A。,接着再消除不增 加4,索引的所有左递归。它消除所有A,一A,Y,其中≤i形式的规则。如果按这样操作从1到m 的每一个,则由于这样的循环的每个步骤只增加索引,且不能再次到达原始索引,因此就不 会留下任何递归循环了。程序清单43是这个算法的详细步骤
情况1:简单直接左递归 在这种情况下,左递归只出现在格式 A→Aa | b 的文法规则中,其中 a和b是终结符和非终结符的串,而且 b不以A开头。在3 . 2 . 3节中,我们看 到这个文法规则生成了格式b an (n≥0)的串。选择A→b是基本情况,而A→Aa是递归情况。 为了消除左递归,将这个文法规则重写为两个规则:一个是首先生成 b,另一个是生成a的 重复,它不用左递归却用右递归: A →bA¢ A ¢→aA¢ | 例4.1 再次考虑在简单表达式文法中的左递归规则: exp → exp addop term | t e r m 它属于格式A → Aa | b,且A = e x p,a = addop term,b = t e r m。将这个规则重写以消除左递归, 就可得到 exp → term exp¢ e x p¢ → addop term exp¢ | 情况2:普遍的直接左递归 这种情况发生在有如下格式的产生式 A → Aa1 | Aa2 | . . . | Aan | b1 | b2 | . . . | bm 中。其中b1 , . . . , bm 均不以A开头。在这种情况下,其解法与简单情况类似,只需将选择相应地 扩展: A →b1 A¢ | b2 A¢ | . . . | bm A¢ A¢ →a1 A¢ | a2 A¢ | . . . | an A¢ | 例4.2 考虑文法规则 exp → exp + term | exp - term | t e r m 如下消除左递归: exp → term exp¢ e x p¢ → + term exp¢ | - term exp¢ | 情况3:一般的左递归 这里描述的算法仅是指不带有 产生式且不带有循环的文法,其中循环( c y c l e)是至少有 一步是以相同的非终结符:A Þ aÞ*A开始和结束的推导。循环几乎肯定能导致分析程序进入 无穷循环,而且带有循环的文法从不作为程序设计语言文法出现。程序设计语言文法确实是有 产生式,但这经常是在非常有限的格式中,所以这个算法对于这些文法也几乎总是有效的。 该算法的方法是:为语言的所有非终结符选择任意顺序,如 A1 , . . . , Am,接着再消除不增 加Ai ¢ 索引的所有左递归。它消除所有 Ai→Aj g,其中j≤i 形式的规则。如果按这样操作从 1到m 的每一个i,则由于这样的循环的每个步骤只增加索引,且不能再次到达原始索引,因此就不 会留下任何递归循环了。程序清单4 - 3是这个算法的详细步骤。 1 1 8 编译原理及实践 下载

China-pub.com 第4章自顶向下的分析 119 下载 程序清单43普遍左递归消除的算法 -1 do replace each era mar rule choice of the form AA B by the rule a B.whtere Ajal a...ar is remvediate recu oing 例4.3考虑下面的文法: A-BalAalc B→Bb|AbId (由于该情况在任何标准程序设计语言中都不会发生,所以这个文法完全是自造的)。 为了使用算法,就须令B的数比A的数大(即A,=A,且A:=B)。因为n=2,则图4-3中的 算法的外循环执行两次,一次是当i=1,另一次是当i=2。当i=1时,不执行内循环(带有素 引),这样唯一的动作就是消除4的直接左递归。最后得到的文法是 A→BaA'cA' A→aA'Ie B→Bb1Ab1d 现在为1=2执行外循环,且还执行一次内循环,此时=1。在这种情况下,我们通过用第1个 规则中的选择替换A而省略了规则B一Ab。因此就得到了文法 A→BacA A”aA'e B→BblBaA'bIcA"bId 最后消除B的直接左递归以得到 A→BaA'|c A→aAe B→cA'bBldB B→bB|aA'bB|E 这个文法没有左递归。 左递归消除并不改变正被识别的语言,但它却改变了文法和分析树。这种改变确实导致了 分析程序变得复杂起来(对于分析程序设计人员而言,也更困难了)。例如在前面作为标准示 例的简单表达式文法中,该文法是左递归的,表达运算的结合性的表达式也是左递归。若要像 在例4.1中一样消除直接左递归,就可得到图41中所给出的文法。 ep→term exp' exp'addop term exp' addop一+|- tem→factor term term'-mulop factor term' mulop-* factor(ep)|number 图4】消除了左递归的简单算术表达式文法
程序清单4-3 普遍左递归消除的算法 例4.3 考虑下面的文法: A → B a | A a | c B → B b | A b | d (由于该情况在任何标准程序设计语言中都不会发生,所以这个文法完全是自造的)。 为了使用算法,就须令B的数比A的数大(即A1 = A,且A2 = B)。因为n = 2,则图4 - 3中的 算法的外循环执行两次,一次是当i = 1,另一次是当i = 2。当i = 1时,不执行内循环(带有索 引j),这样唯一的动作就是消除A的直接左递归。最后得到的文法是 A →B a A¢ | c A¢ A¢ → a A¢ | B → B b | A b| d 现在为i = 2执行外循环,且还执行一次内循环,此时 j = 1。在这种情况下,我们通过用第 1个 规则中的选择替换A而省略了规则B→A b。因此就得到了文法 A →B a A¢ | c A¢ A¢ → a A¢ | B → B b | B a A¢b | c A¢b | d 最后消除B的直接左递归以得到 A → B a A¢ | c A¢ A¢ → a A¢| B → c A¢ b B¢ | d B¢ B¢ → b B¢ | a A¢b B¢ | 这个文法没有左递归。 左递归消除并不改变正被识别的语言,但它却改变了文法和分析树。这种改变确实导致了 分析程序变得复杂起来(对于分析程序设计人员而言,也更困难了)。例如在前面作为标准示 例的简单表达式文法中,该文法是左递归的,表达运算的结合性的表达式也是左递归。若要像 在例4 . 1中一样消除直接左递归,就可得到图4 - 1中所给出的文法。 exp → t e r m e x p¢ e x p¢ → a d d o p t e r m e x p¢ | a d d o p → + | - t e r m → f a c t o r t e r m¢ t e r m¢ → m u l o p f a c t o r t e r m¢ | m u l o p → * f a c t o r → ( exp ) | n u m b e r 图4-1 消除了左递归的简单算术表达式文法 第 4章 自顶向下的分析 1 1 9 下载