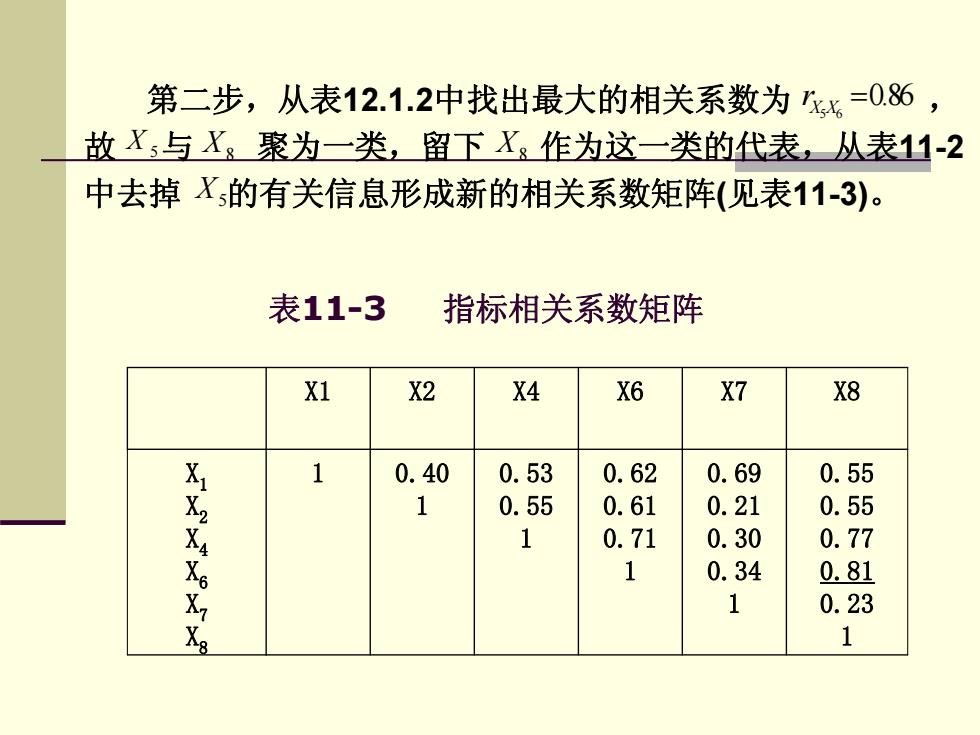
第二步,从表12.1.2中找出最大的相关系数为kx=0.86, 故X与X:聚为一类,留下X:作为这一类的代表,丛表11-2 中去掉X的有关信息形成新的相关系数矩阵(见表11-3)。 表11-3 指标相关系数矩阵 X1 X2 X4 X6 X7 X8 1 0.40 0.53 0.62 0.69 0.55 0.55 0.61 0.21 0.55 1 0.71 0.30 0.77 1 0.34 0.81 1 0.23 1
第二步,从表12.1.2中找出最大的相关系数为 , 故 与 聚为一类,留下 作为这一类的代表,从表11-2 中去掉 的有关信息形成新的相关系数矩阵(见表11-3)。 5 6 0.86 X X r = X 5 X8 X8 X5 表11-3 指标相关系数矩阵 X1 X2 X4 X6 X7 X8 X1 X2 X4 X6 X7 X8 1 0.40 1 0.53 0.55 1 0.62 0.61 0.71 1 0.69 0.21 0.30 0.34 1 0.55 0.55 0.77 0.81 0.23 1

■ 第三步,表11-3中最大的相关系数为x,x=0.81,所 以X6与X8聚成一类,由于X8已与X聚成一类了,所 以该步实际上是将XX6X聚为一类。 ■重复这一过程,直至将所有指标聚为一类为止。由于 有8个指标,所以需要七步(第四步至第七步聚类过程 从略)。最终形成聚类图(谱系图)如图1-1所示。 0.5+ 346 58 指标序号 图11-1 聚类图(谱系图)小
第三步,表11-3中最大的相关系数为 ,所 以 与 聚成一类,由于 已与 聚成一类了,所 以该步实际上是将 聚为一类。 重复这一过程,直至将所有指标聚为一类为止。由于 有8个指标,所以需要七步(第四步至第七步聚类过程 从略)。最终形成聚类图(谱系图)如图1-1所示。 6 8 0.81 X X r = X6 X8 X8 X5 X5 X6 X8

11.2.1.2评价指标的选择方法 第三种方法:主成分分析法 ■主成分分析就是设法将原来众多的具有一定相关性的 指标(比如p个指标),重新组合成一组新的相互无关的 综合指标来代替原来的指标。 ■ 主成分分析计算步骤如下: ①由已知的原始数据矩阵X计算样本均值向量 立=x=(低,m)'(11-1)其中元=∑x,=12,m) ②计算样本协方差矩阵立=n一,)o, (11-2)其中 号,=2(x,-xx,-)6j=12,m)
第三种方法:主成分分析法 主成分分析就是设法将原来众多的具有一定相关性的 指标(比如p个指标),重新组合成一组新的相互无关的 综合指标来代替原来的指标。 主成分分析计算步骤如下: ①由已知的原始数据矩阵 计算样本均值向量 (11-1)其中 ②计算样本协方差矩阵 (11-2)其中 X n m× 1 2 ˆ (, , , ) T m μ = = x xx x L 1 1 ( 1, 2, , ) n i ij j x xi m n = = = ∑ L 1 ˆ () ( ) ˆ 1 V sij ij n = = σ − 1 ( )( ) ( , 1, 2, , ) n ij li i lj j l s x xx x i j m = = −− = ∑ L 11.2.1.2 评价指标的选择方法

11.2.1.2评价指标的选择方法 ③把原始数据标准化,即玉,=一王记京m=低,) (11-3) 形成样本相关矩阵=?;(11-4) ■ ④求的P特征根1≥2≥.≥m≥0及相应的标准正交化的 特征向量4,.,4m,可得主成分为y=4,x(i=1,2,.,m)。 (11-5)
③把原始数据标准化,即 记 。 (11-3) 形成样本相关矩阵 ; (11-4) ④求的 特征根 及相应的标准正交化的 特征向量 ,可得主成分为 。 (11-5) ij j ij jj x x x σ − % = ( ) X x % n m ij × = % ˆ T R XX = % % 1 2 0 λ ≥≥≥ ≥ λ λ L m R ˆ 1 2 , m uu u L ( 1, 2, , ) T i i y u xi m = = L 11.2.1.2 评价指标的选择方法