《纺织复合材料》课程参考文献（Mechanics of Composite Materials with MATLAB）13 Solutions to Problems

Solutions to Problems 225 16 P=1 14 p=2.eta=0.4 p=2eta=0.5 p=2,eta=0.6 p=3 10 0 0 6 Qw-G 0.2 0.4 0.6 0.8 Fig.Variation of E2 versus V for Problem 3.6 >v(11)=E2(1,14.8,3.45,0,0.3,0.3,0.36,85.6,3) v 3.45004.15644.60415.07675.62496.28787.1155 8.18459.622811.665714.8000 >x=[0;0.1;0.2;0.3;0.4;0.5;0.6;0.70.8; 0.9;1] 0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000 1.0000

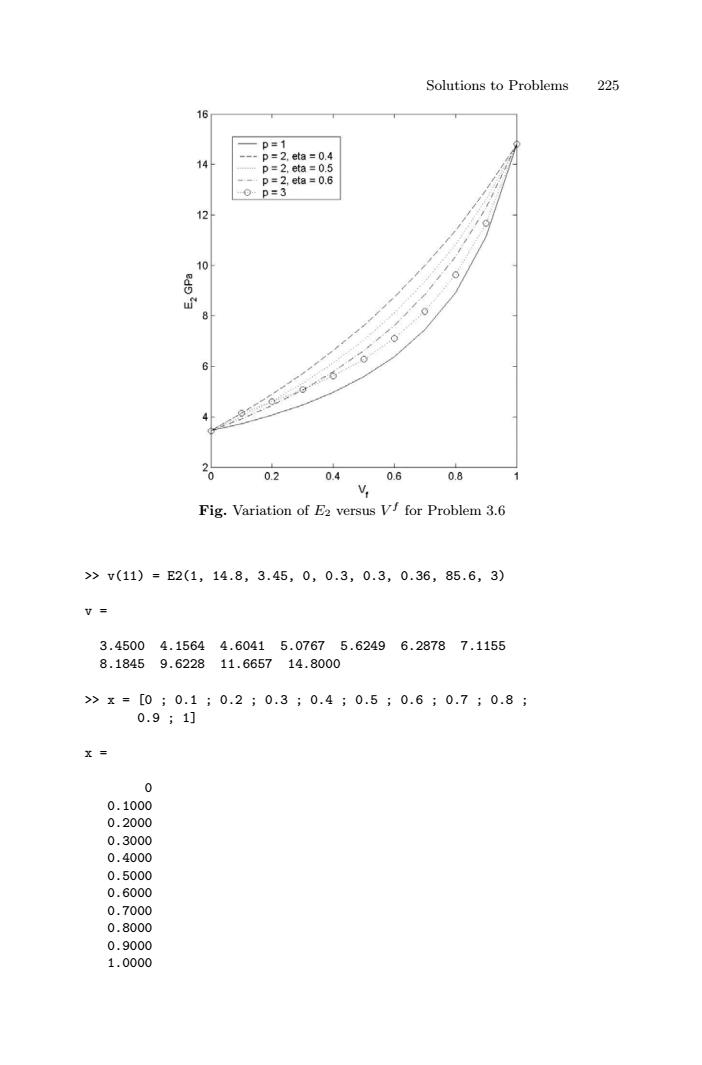
Solutions to Problems 225 Fig. Variation of E2 versus V f for Problem 3.6 >> v(11) = E2(1, 14.8, 3.45, 0, 0.3, 0.3, 0.36, 85.6, 3) v = 3.4500 4.1564 4.6041 5.0767 5.6249 6.2878 7.1155 8.1845 9.6228 11.6657 14.8000 >> x = [0 ; 0.1 ; 0.2 ; 0.3 ; 0.4 ; 0.5 ; 0.6 ; 0.7 ; 0.8 ; 0.9 ; 1] x = 0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000 1.0000

226 Solutions to Problems >plot(x,y,k-’,x,z,k-’,x,w,k:’,x,u,k-.’,x,,‘k0:) >xlabel('V_f'); >ylabel('E_2 GPa'); >1 egend(‘p=1',‘p=2,eta=0.4',‘p=2,eta=0.5’, ‘p=2,eta=0.6’,‘p=3',5); Problem 3.7 The shear modulus G12 is calculated in GPa using three different formulas using the MATLAB function G12 as follows.Notice that the second and third values obtained are very close. >G12(0.55,28.3,1.27,0,1) ans 2.6755 >G12(0.55,28.3,1.27,0.6,2) ans 3.5340 >G12(0.55,28.3,1.27,0,3) ans 3.8382 Problem 3.8 >y(1)=G12(0,28.3,1.27,0,1) y= 1.2700 >>y(2)=G12(0.1,28.3,1.27,0,1) y= 1.27001.4041 >y(3)=G12(0.2,28.3,1.27,0,1)

226 Solutions to Problems >> plot(x,y,‘k-’,x,z,‘k--’,x,w,‘k:’,x,u,‘k-.’,x,v,‘ko:’) >> xlabel(‘V_f’); >> ylabel(‘E_2 GPa’); >> legend(‘p = 1’, ‘p = 2, eta = 0.4’, ‘p = 2, eta = 0.5’, ‘p = 2, eta = 0.6’, ‘p = 3’, 5); Problem 3.7 The shear modulus G12 is calculated in GPa using three different formulas using the MATLAB function G12 as follows. Notice that the second and third values obtained are very close. >> G12(0.55, 28.3, 1.27, 0, 1) ans = 2.6755 >> G12(0.55, 28.3, 1.27, 0.6, 2) ans = 3.5340 >> G12(0.55, 28.3, 1.27, 0, 3) ans = 3.8382 Problem 3.8 >> y(1) = G12(0, 28.3, 1.27, 0, 1) y = 1.2700 >> y(2) = G12(0.1, 28.3, 1.27, 0, 1) y = 1.2700 1.4041 >> y(3) = G12(0.2, 28.3, 1.27, 0, 1)

Solutions to Problems 227 y= 1.27001.40411.5699 >>y(4)=G12(0.3,28.3,1.27,0,1) y= 1.27001.40411.56991.7801 >y(5)=G12(0.4,28.3,1.27,0,1) y= 1.27001.40411.56991.78012.0552 >y(6)=G12(0.5,28.3,1.27,0,1) y= 1.27001.40411.56991.78012.05522.4309 >>y(7)=G12(0.6,28.3,1.27,0,1) y= 1.27001.40411.56991.78012.05522.43092.9748 >>y(8)=G12(0.7,28.3,1.27,0,1) y= 1.27001.40411.56991.78012.05522.43092.9748 3.8321 >y(9)=G12(0.8,28.3,1.27,0,1) y= 1.27001.40411.56991.78012.05522.43092.9748 3.83215.3836 >y(10)=G12(0.9,28.3,1.27,0,1) y= 1.27001.40411.56991.78012.05522.43092.9748 3.8321 5.38369.0463

Solutions to Problems 227 y = 1.2700 1.4041 1.5699 >> y(4) = G12(0.3, 28.3, 1.27, 0, 1) y = 1.2700 1.4041 1.5699 1.7801 >> y(5) = G12(0.4, 28.3, 1.27, 0, 1) y = 1.2700 1.4041 1.5699 1.7801 2.0552 >> y(6) = G12(0.5, 28.3, 1.27, 0, 1) y = 1.2700 1.4041 1.5699 1.7801 2.0552 2.4309 >> y(7) = G12(0.6, 28.3, 1.27, 0, 1) y = 1.2700 1.4041 1.5699 1.7801 2.0552 2.4309 2.9748 >> y(8) = G12(0.7, 28.3, 1.27, 0, 1) y = 1.2700 1.4041 1.5699 1.7801 2.0552 2.4309 2.9748 3.8321 >> y(9) = G12(0.8, 28.3, 1.27, 0, 1) y = 1.2700 1.4041 1.5699 1.7801 2.0552 2.4309 2.9748 3.8321 5.3836 >> y(10) = G12(0.9, 28.3, 1.27, 0, 1) y = 1.2700 1.4041 1.5699 1.7801 2.0552 2.4309 2.9748 3.8321 5.3836 9.0463

228 Solutions to Problems >y(11)=G12(1,28.3,1.27,0,1) y= Columns 1 through 10 1.27001.40411.56991.78012.05522.43092.9748 3.83215.38369.0463 Column 11 28.3000 >z(1)=G12(0,28.3,1.27,0.6,2) z= 1.2700 >z(2)=G12(0.1,28.3,1.27,0.6,2) 2= 1.27001.4928 >>z(3)=G12(0.2,28.3,1.27,0.6,2) z= 1.27001.49281.7661 >>z(4)=G12(0.3,28.3,1.27,0.6,2) 2= 1.27001.49281.76612.1095 >z(5)=G12(0.4,28.3,1.27,0.6,2) z= 1.27001.49281.76612.10952.5538 >z(6)=G12(0.5,28.3,1.27,0.6,2) z= 1.27001.49281.76612.10952.55383.1510

228 Solutions to Problems >> y(11) = G12(1, 28.3, 1.27, 0, 1) y = Columns 1 through 10 1.2700 1.4041 1.5699 1.7801 2.0552 2.4309 2.9748 3.8321 5.3836 9.0463 Column 11 28.3000 >> z(1) = G12(0, 28.3, 1.27, 0.6, 2) z = 1.2700 >> z(2) = G12(0.1, 28.3, 1.27, 0.6, 2) z = 1.2700 1.4928 >> z(3) = G12(0.2, 28.3, 1.27, 0.6, 2) z = 1.2700 1.4928 1.7661 >> z(4) = G12(0.3, 28.3, 1.27, 0.6, 2) z = 1.2700 1.4928 1.7661 2.1095 >> z(5) = G12(0.4, 28.3, 1.27, 0.6, 2) z = 1.2700 1.4928 1.7661 2.1095 2.5538 >> z(6) = G12(0.5, 28.3, 1.27, 0.6, 2) z = 1.2700 1.4928 1.7661 2.1095 2.5538 3.1510

Solutions to Problems 229 >>z(7)=G12(0.6,28.3,1.27,0.6,2) z= 1.27001.49281.76612.10952.55383.15103.9966 >>z(8)=G12(0.7,28.3,1.27,0.6,2) z= 1.27001.49281.76612.10952.55383.15103.9966 5.2863 >z(9)=G12(0.8,28.3,1.27,0.6,2) z= 1.27001.49281.76612.10952.55383.15103.9966 5.28637.4945 >>z(10)=G12(0.9,28.3,1.27,0.6,2) 2= 1.27001.49281.76612.10952.55383.15103.9966 5.28637.494512.1448 >z(11)=G12(1,28.3,1.27,0.6,2) 2= Columns 1 through 10 1.27001.49281.76612.10952.55383.15103.9966 5.28637.494512.1448 Column 11 28.3000 >(1)=G12(0,28.3,1.27,0,3) w= 1.2700

Solutions to Problems 229 >> z(7) = G12(0.6, 28.3, 1.27, 0.6, 2) z = 1.2700 1.4928 1.7661 2.1095 2.5538 3.1510 3.9966 >> z(8) = G12(0.7, 28.3, 1.27, 0.6, 2) z = 1.2700 1.4928 1.7661 2.1095 2.5538 3.1510 3.9966 5.2863 >> z(9) = G12(0.8, 28.3, 1.27, 0.6, 2) z = 1.2700 1.4928 1.7661 2.1095 2.5538 3.1510 3.9966 5.2863 7.4945 >> z(10) = G12(0.9, 28.3, 1.27, 0.6, 2) z = 1.2700 1.4928 1.7661 2.1095 2.5538 3.1510 3.9966 5.2863 7.4945 12.1448 >> z(11) = G12(1, 28.3, 1.27, 0.6, 2) z = Columns 1 through 10 1.2700 1.4928 1.7661 2.1095 2.5538 3.1510 3.9966 5.2863 7.4945 12.1448 Column 11 28.3000 >> w(1) = G12(0, 28.3, 1.27, 0, 3) w = 1.2700