
2.2线性表的顺序存储及操作实现 2.2.1顺序存储 线性表的顺序存储是把线性表的数据元 素放在一组地址连续的存储单元中。(以元 素在计算机内存储器内的物理位置来体现互 为前驱和后继的逻辑关系,线性表中相邻的 元素在内存储器内也相邻) 假设每个元素占用1(小写L)个存储单 元,线性表中第一个元素的存储地址 L0C(al)=b,那麽线性表中第i个元素的存储 地址是多少?
2.2线性表的顺序存储及操作实现 2.2.1 顺序存储 线性表的顺序存储是把线性表的数据元 素放在一组地址连续的存储单元中。(以元 素在计算机内存储器内的物理位置来体现互 为前驱和后继的逻辑关系,线性表中相邻的 元素在内存储器内也相邻) 假设每个元素占用l( 小写L)个存储单 元,线性表中第一个元素的存储地址 LOC(a1)=b,那麽线性表中第i个元素的存储 地址是多少?
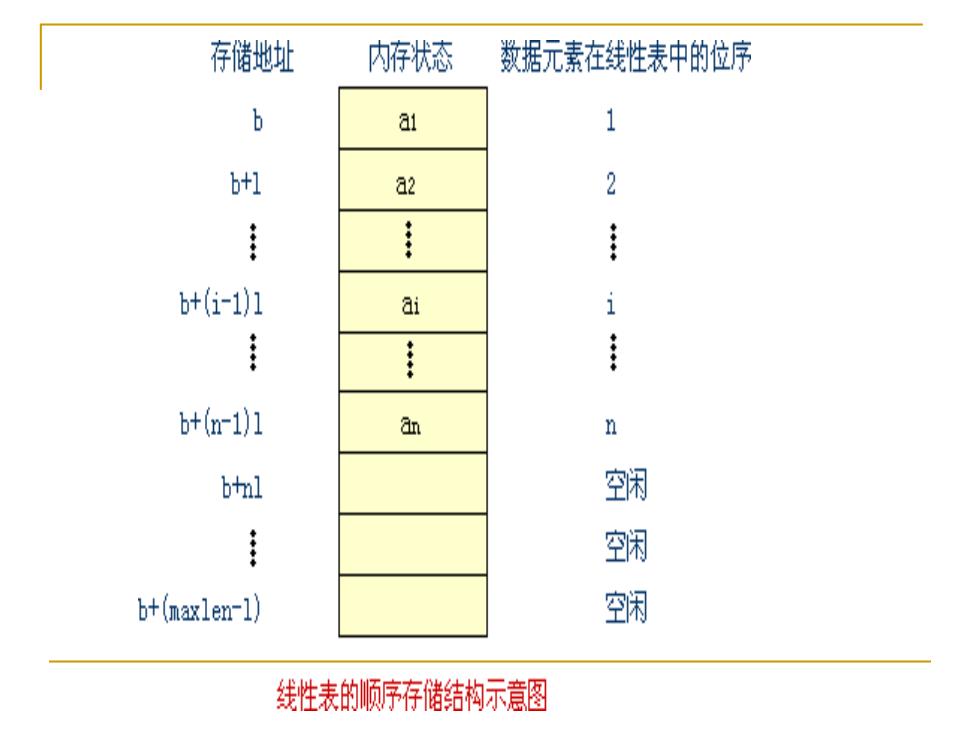
存储地址 内存状态 数据元素在线性表中的位序 b ai b+l a2 2 b+(i-1)l ai i bt(n-101 an btnl 空闲 空闲 bt(maxlen-l) 空闲 线性表的顺序存储结构示意图

因为是在java语言的层面上讨论问题(不是在机器语 言的层面上,存储单元的编号即地址对我们来说是透 明的,不可见的) ■在java虚拟处理器中我们认为线性表的顺序存储是把 线性表的数据元素放在一维数组中,(数组占用的就 是一组地址连续的存储单元)数据元素在数组中相邻 就表示它们在线性表中互为前驱和后继。 。在抽象数据类型的定义中讲过:定义于逻辑结构上的 基本操作不能实现,存储结构确定了之后才能实现。 下面就来讨论在顺序存储结构下基本操作的实现。重 点讨论插入和删除两种操作
◼ 因为是在java语言的层面上讨论问题(不是在机器语 言的层面上,存储单元的编号即地址对我们来说是透 明的,不可见的) ◼ 在java虚拟处理器中我们认为线性表的顺序存储是把 线性表的数据元素放在一维数组中,(数组占用的就 是一组地址连续的存储单元) 数据元素在数组中相邻 就表示它们在线性表中互为前驱和后继。 ◼ 在抽象数据类型的定义中讲过:定义于逻辑结构上的 基本操作不能实现,存储结构确定了之后才能实现。 下面就来讨论在顺序存储结构下基本操作的实现。重 点讨论插入和删除两种操作
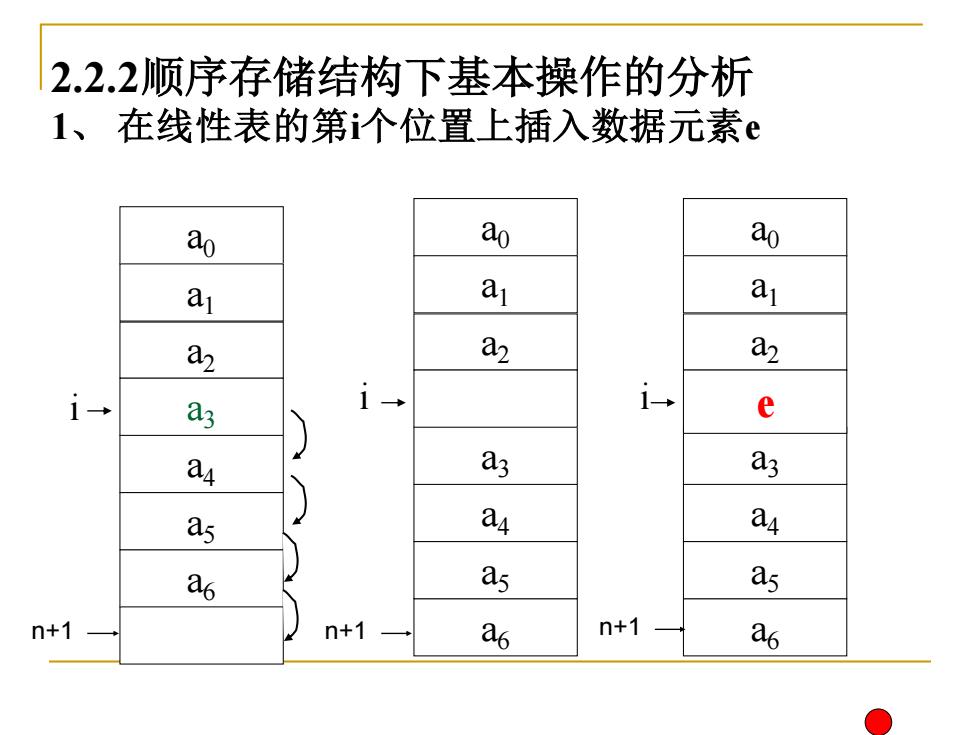
2.2.2顺序存储结构下基本操作的分析 1、在线性表的第i个位置上插入数据元素e ao ao ao a a a a2 a2 a i→ ag i i e ay a ag as ay ay a6 as as n+1 n+1 as n+1 as
i a0 a1 a2 a6 a5 a4 a3 a0 a1 a2 a6 i a5 a4 a3 a0 a1 a2 a6 i a5 a4 a3 e n+1 n+1 n+1 2.2.2顺序存储结构下基本操作的分析 1、 在线性表的第i个位置上插入数据元素e

■?分析插入数据元素到线性表(即数组)的第个位置上所需移动 元素次数: ■答:从第i个数据元素到第n个都需移动,共需移动n-i+1次 ■?每一个位置上都有可能插入数据元素,平均移动次数是多少? ■答:第一个位置上n次,第二个位置上n-1次,第三个位置上n-2次 ,依次类推,第+1个位置上0次,平均移动次数为: ■[n+(n-1)+.+1]/n+1=n/2,即: ∑j n(n+1) 平均移动次数 .2 n n+1 n+1 2
◼ ?分析插入数据元素到线性表(即数组)的第i个位置上所需移动 元素次数: ◼ 答:从第 i个数据元素到第n 个都需移动,共需移动n-i+1次 ◼ ?每一个位置上都有可能插入数据元素,平均移动次数是多少? ◼ 答:第一个位置上n次,第二个位置上n-1次,第三个位置上n-2次 ,依次类推,第n+1个位置上0次,平均移动次数为: ◼ [n+(n-1)+.+1]/n+1=n/2 , 即: ◼ ◼ 2 n n 1 2 n(n 1) n 1 j n j 1 = + + = + = 平均移动次数 =