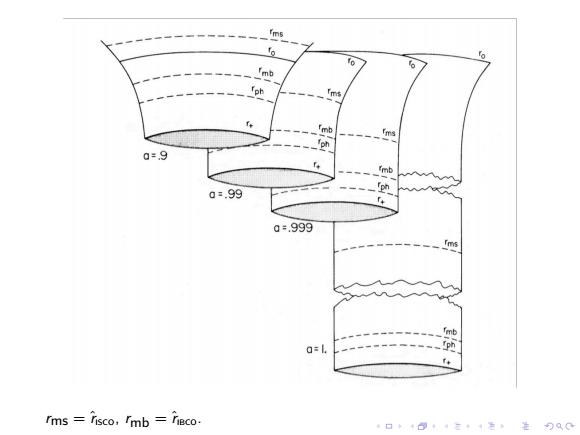
ms fmb ph mb ms ph a=9 0.99 a=.999 mb rms risco.Imb heco. 4口◆4回4三+1声,¥)QC
. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. rms = ˆr . ISCO, rmb = ˆrIBCO

Kerr spacetime In terms of Boyer-Lindquist coordinates,7,0,the metric of a Kerr spacetime is de(12Cia +(+2GM327sin20. sinGMasind where △=P-2GM+a2,∑=2+a2cos20, and a is the Kerr parameter a=J/M. For a near extreme Kerr BH,introduce a parameter <<1. The ISCO and IBCO have different scaling behaviors under A-0 limit GM+21/3,23GM+0A) GM+21/2λGM+o(). This motivates us to consider two different limits of near horizon geometry. 口卡三4色至习Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Kerr spacetime In terms of Boyer-Lindquist coordinates ˆt,ˆr, θ, ϕˆ, the metric of a Kerr spacetime is ds2 = −(1 − 2GMˆr Σ )dˆt + Σ ∆ dˆr 2 + Σdθ 2 + +(ˆr 2 + a 2 + 2GMa2ˆrsin2 θ Σ )sin2 θdϕˆ2 − 4GMaˆrsin2 θ Σ dˆtdϕˆ where ∆ ≡ ˆr 2 − 2GMˆr + a 2 , Σ ≡ ˆr 2 + a 2 cos2 θ, and a is the Kerr parameter a = J/M. For a near extreme Kerr BH, introduce a parameter λ = √ 1 − J 2 M4 << 1. The ISCO and IBCO have different scaling behaviors under λ → 0 limit ˆrISCO = GM + 21/3λ 2/3GM + O(λ) ˆrIBCO = GM + 21/2λGM + o(λ). This motivates us to consider two different limits of near horizon geometry

NHEK:near horizon geometry of extreme Kerr Taking the high spin limit入→O, T-嘉,R-,=- M we get the NEHK geometryJ.M.Be G.T.HroM0 ds2 =2MT(0) (-Rar+e+ar+A2o(d0+an where the polar functions are T(0)= 1+cos20 2sin0 2 A(0)= 1+cos20' Obviously it has enhanced SL(2,R)x U(1)symmetry. 口◆4回t1三1声,¥99C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . NHEK: near horizon geometry of extreme Kerr Taking the high spin limit λ → 0, T = ˆt 2M λ 2/3 , R = ˆr −ˆr+ M λ −2/3 , Φ = ϕˆ − ˆt 2M , we get the NEHK geometryJ. M. Bardeen and G.T. Horowitz 9905099 ds2 = 2M2Γ(θ) ( −R 2 dT2 + dR2 R2 + dθ 2 + Λ2 (θ)(dΦ + RdT) 2 ) , where the polar functions are Γ(θ) = 1 + cos2 θ 2 , Λ(θ) = 2 sin θ 1 + cos2 θ . Obviously it has enhanced SL(2, R) × U(1) symmetry

Near-NHEK:very near horizon region We may take a different limit:入-→0,fixed t二 2MK -i4,重=6-2 t we will find the near-NHEK geometry:L Bredbers etal.0907.3 ds2 =2MPT(0) dr2 r+2xue+2四+d+Aoo++a9) where >0 is arbitrary as a consequence of emerging scale invariance. The near-NHEK is closer to the horizon than the NHEK.It has enhanced SL(2,R)U(1)symmetry as well. Besides the enhanced symmetry,there is a discrete PT-symmetry in both NHEK and near-NHEK geometries: T→-T,Φ-ΦNHEK t→-t,p→-near-NHEK 口卡+·三4色,在习80
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Near-NHEK: very near horizon region We may take a different limit: λ → 0, κ fixed t = ˆt 2Mκ λ, r = κ ˆr −ˆr+ Mλ , Φ = ϕˆ − ˆt 2M , we will find the near-NHEK geometry: I. Bredberg et.al. 0907.3477 ds2 = 2M2Γ(θ) ( −r(r + 2κ)dt2 + dr2 r(r + 2κ) + dθ 2 + Λ2 (θ)(dϕ + (r + κ)dt) 2 ) , where κ > 0 is arbitrary as a consequence of emerging scale invariance. The near-NHEK is closer to the horizon than the NHEK. It has enhanced SL(2, R) × U(1) symmetry as well. Besides the enhanced symmetry, there is a discrete PT-symmetry in both NHEK and near-NHEK geometries: T → −T, Φ → −Φ NHEK t → −t, ϕ → −ϕ near-NHEK
Remarks The NHEK and near-NHEK has played key roles in setting up the Kerr/CFT correspondence.M.Gulca et00.4266.Bredberg et0074ad c-s ch1001320 4口◆4回t1三1声,¥QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Remarks The NHEK and near-NHEK has played key roles in setting up the Kerr/CFT correspondence. M. Guica et.al. 0809.4266,I. Bredberg et.al. 0907.3477,BC and C-S Chu 1001.3208 Due to the enhanced symmetry, the motion of the point particles can be classified. It turns out to be that the trajectories in such geometry could be related to each other by conformal transformations and PT transformations. A.P. Porfyriadis and A. Strominger 1401.3746,... Very recently G. Compere et.al. studied the gravitational wave in the final stages of EMRIs of non-spinning compact objects into supermassive nearly extremal Kerr BH. G. Compere et.al. 1712.0713 ▶ Geodesic approximation: no internal structure of the compact object, no backreaction ▶ Consider GWs at different stages using Teukolsky’s formalism: asymp. flat ⇒ NHEK ⇒ near-NHEK ▶ Paste GWs in different stages The same treatment can be applied to high spin IMRACs, but