
Preliminary Basic Data Model:Sets Many similarity problems can be couched as finding subsets of some universal set that have significant intersection. Examples include: 1.Documents represented by their sets of shingles (or hashes of those shingles). 2.Similar customers or products
Basic Data Model: Sets • Many similarity problems can be couched as finding subsets of some universal set that have significant intersection. • Examples include: 1. Documents represented by their sets of shingles (or hashes of those shingles). 2. Similar customers or products. Minhashing Preliminary
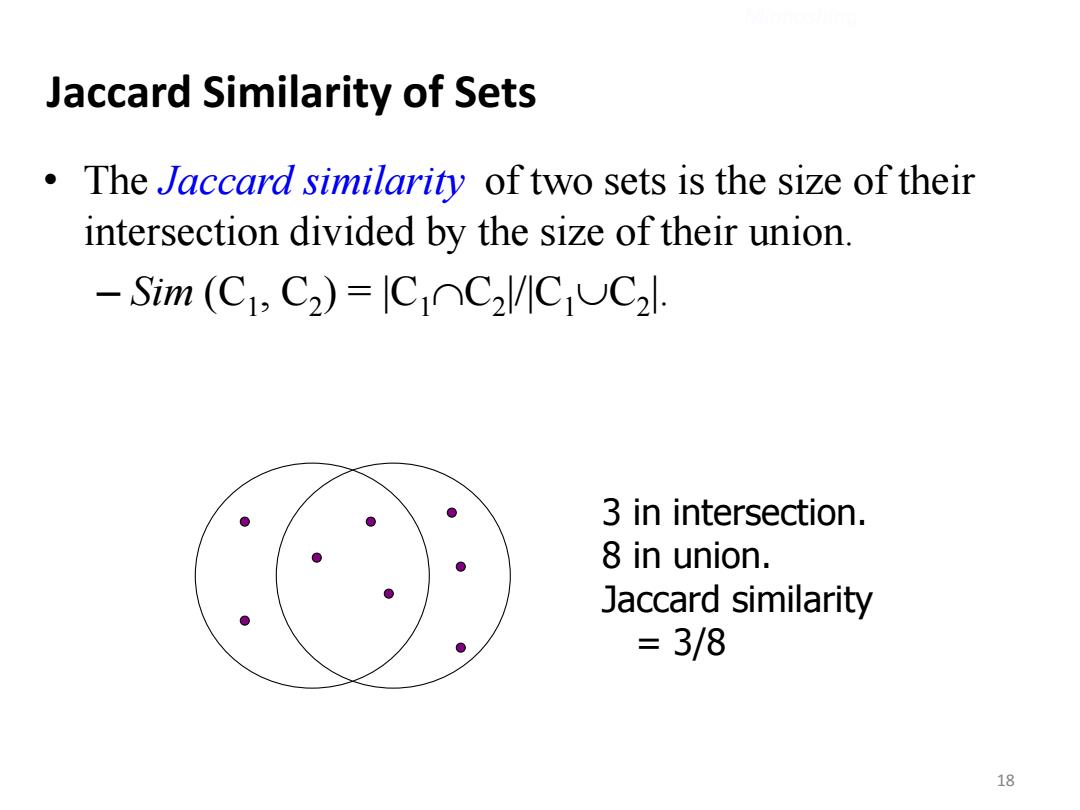
Jaccard Similarity of Sets The Jaccard similarity of two sets is the size of their intersection divided by the size of their union. -Sim (C1,C2)=ICOC2l/ICIUC21. 3 in intersection. 8 in union. Jaccard similarity =3/8 18
18 Jaccard Similarity of Sets • The Jaccard similarity of two sets is the size of their intersection divided by the size of their union. – Sim (C1 , C2 ) = |C1C2 |/|C1C2 |. Minhashing 3 in intersection. 8 in union. Jaccard similarity = 3/8

From Sets to Boolean Matrices Rows elements of the universal set. ·Columns=sets. 1 in row e and column s if and only if e is a member of S. Column similarity is the Jaccard similarity of the sets of their rows with 1. Typical matrix is sparse. 19
19 From Sets to Boolean Matrices • Rows = elements of the universal set. • Columns = sets. • 1 in row e and column S if and only if e is a member of S. • Column similarity is the Jaccard similarity of the sets of their rows with 1. • Typical matrix is sparse. Minhashing

Example:Jaccard Similarity of Columns C1 C2 01 米 1 0 米 11** Sim(C1vC2)=2/5=0.4 0 0 11** 0 1 米 20
20 Example: Jaccard Similarity of Columns C1 C2 0 1 1 0 1 1 Sim (C1 , C2 ) = 2/5 = 0.4 0 0 1 1 0 1 * * * * * * * Minhashing

When Is Similarity Interesting? ① When the sets are so large or so many that they cannot fit in main memory. ② Or,when there are so many sets that comparing all pairs of sets takes too much time. ③ Or both. 21
21 When Is Similarity Interesting? ① When the sets are so large or so many that they cannot fit in main memory. ② Or, when there are so many sets that comparing all pairs of sets takes too much time. ③ Or both. Minhashing