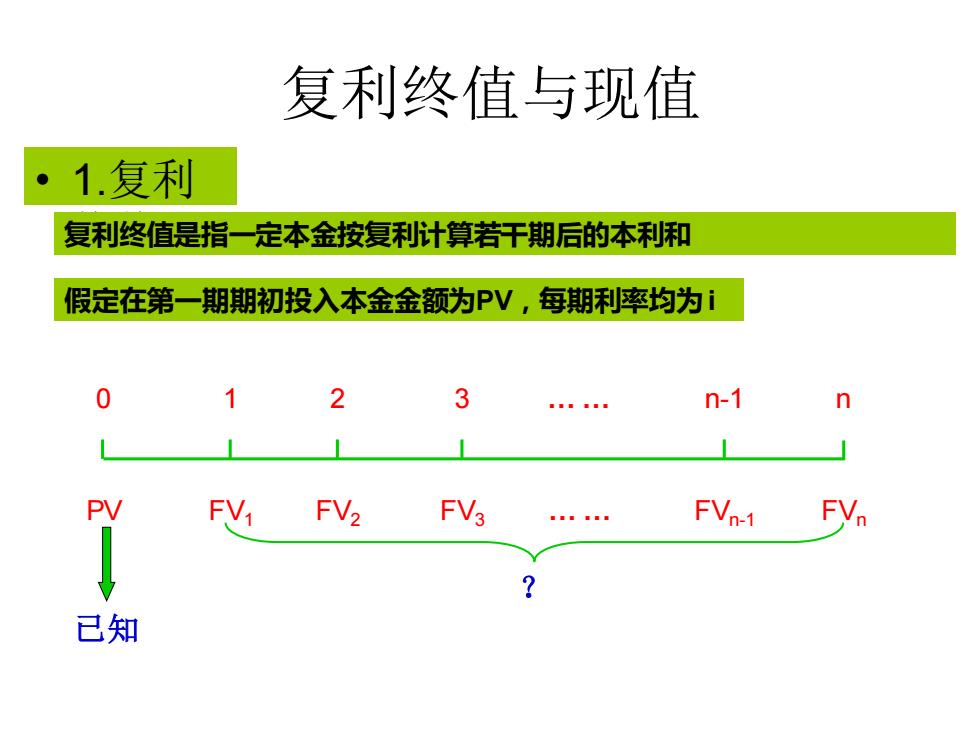
复利终值与现值 1.复利 复利终值是指一定本金按复利计算若干期后的本利和 假定在第一期期初投入本金金额为PV,每期利率均为1 2 3 n-1 n PV FV FV2 FV3 FVn-1 FV 已知
复利终值与现值 • 1.复利 复利终值是指一定本金按复利计算若干期后的本利和 终值 假定在第一期期初投入本金金额为PV,每期利率均为i 0 1 2 3 . . n-1 n PV FV1 FV2 FV3 . . FVn-1 FVn 已知 ?

复利终值推导 第1期终值:FY=PV+Pi=PV(1+i) 第2期终值:FY,=FV+FVi=PV(1+i)+PV(1+i)i=PV(1+i)2 第3期终值:FY,=FY,+FYi=PV(I++PV(1+i=PV(I+识 第n期终值:F刚,=FY,+FVi=PV(I+)+PV1+i)i=PV(I+) 根据上述计算可以推导出,复利终值计算公式为: FV=PV(1+r)n=FVIFr,n 其中n=1,2,3,. FVIFn为复利终值系数
复利终值推导 第1期终值: 第2期终值: 第3期终值: . 第n期终值: (1 ) 1 FV = PV + PVi = PV + i 2 2 1 1 FV = FV + FVi = PV(1+i) + PV(1+i)i = PV(1+i) 2 2 3 3 2 2 FV = FV + FV i = PV(1+ i) + PV(1+ i) i = PV(1+ i) . n n n n n n FV FV FV i PV(1 i) PV(1 i) i PV(1 i) 1 1 = 1 + 1 = + + + = + − − − − 根据上述计算可以推导出,复利终值计算公式为: FV = PV(1 + r)n = FVIFr,n FVIFr,n为复利终值系数 其中n=1,2,3

终值:一般公式 -FV=终值 -PV=现值 一r=每期利率 -T=期数 ·利率终值系数:(1+)
终值: 一般公式 – FV = 终值 – PV = 现值 – r = 每期利率 – T = 期数 • 利率终值系数: (1 + r)t
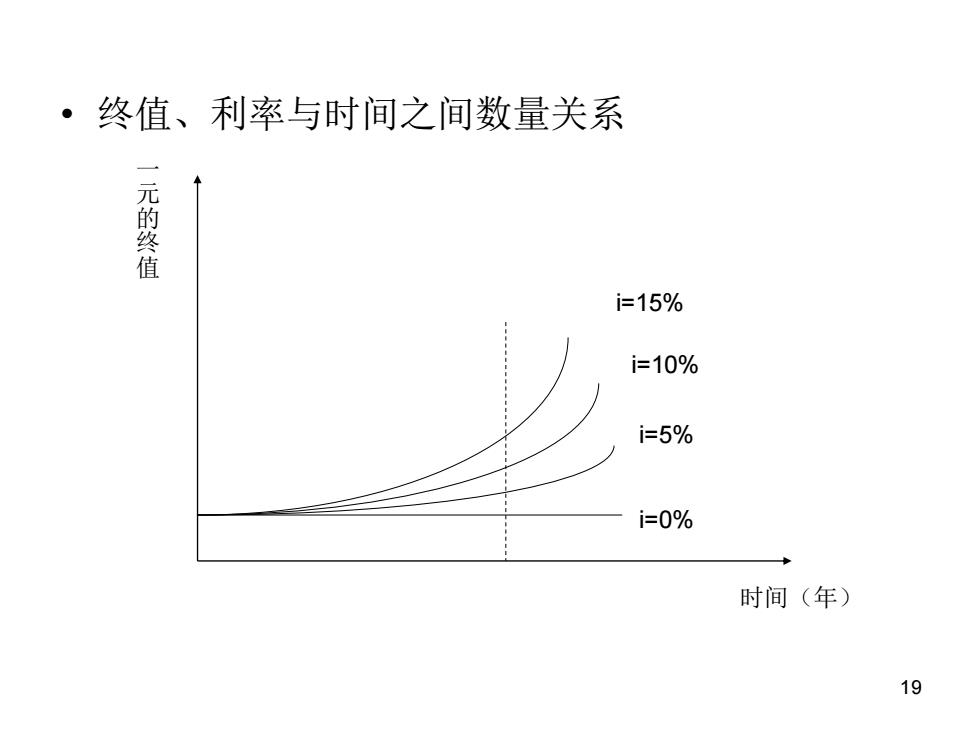
·终值、利率与时间之间数量关系 元的终值 i=15% i=10% i=5% i=0% 时间(年) 19
19 • 终值、利率与时间之间数量关系 时间(年) 一 元 的 终 值 i=0% i=5% i=10% i=15%

复利终值的应用 ·按照复利计息的利息计算式为: FV,-PV=PV[(1+i)”-1] ·考虑计息次数,终值计算式为 FT-PV1 ·如果名义利率为年利率,一年 计息m次,则实际年利率为:
• 按照复利计息的利息计算式为: • 考虑计息次数,终值计算式为 • 如果名义利率为年利率,一年 计息m次,则实际年利率为: [(1 ) 1] n FV PV PV i n − = + − 1 mn n i FV PV m = + 1 1 m i EFF m = + − 复利终值的应用