Dijkstra's algorithm:another example Step N D(v),p(v)D(w),p(w) D(x).p(x)D(y).p(y)D(z).p(z) 0 U 2,U 5,u 1,u 0 o 1 uX← 2,u 4,x 2,X ∞ 2 uXy+ 2,U 3,y 4,y 3 uxyV 3,y 4,y 4 uxyW+ 4,y 5 uxyVWZ+ 5 3 -W- 5 Check out the online interactive exercises for more examples:http://gaia.cs.umass.edu/kurose_ross/interactive/ Network Layer:Control Plane 5-16
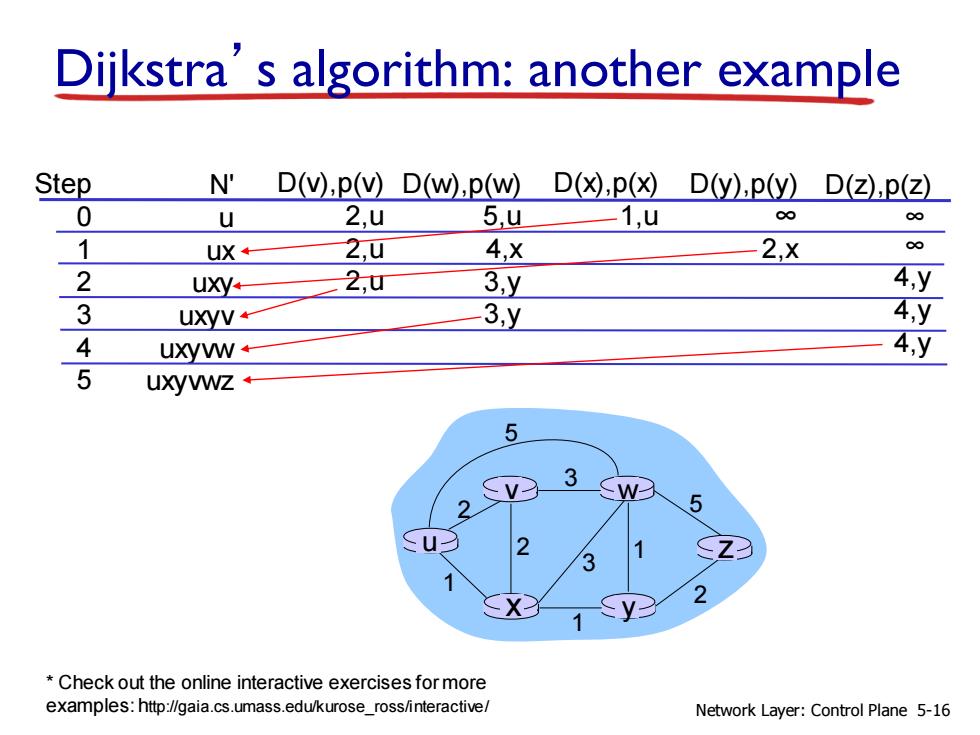
Dijkstra’s algorithm: another example Step 0 1 2 3 4 5 N' u ux uxy uxyv uxyvw uxyvwz D(v),p(v) 2,u 2,u 2,u D(w),p(w) 5,u 4,x 3,y 3,y D(x),p(x) 1,u D(y),p(y) ∞ 2,x D(z),p(z) ∞ ∞ 4,y 4,y 4,y u x y v w z 2 2 1 3 1 1 2 5 3 5 Network Layer: Control Plane 5-16 * Check out the online interactive exercises for more examples: http://gaia.cs.umass.edu/kurose_ross/interactive/
Dijkstra's algorithm:example (2) resulting shortest-path tree from u: &V Su3 <X resulting forwarding table in u: destination link (u,v) X (u,X) y (u,X) W (u,) 2 (u,X) Network Layer:Control Plane 5-17
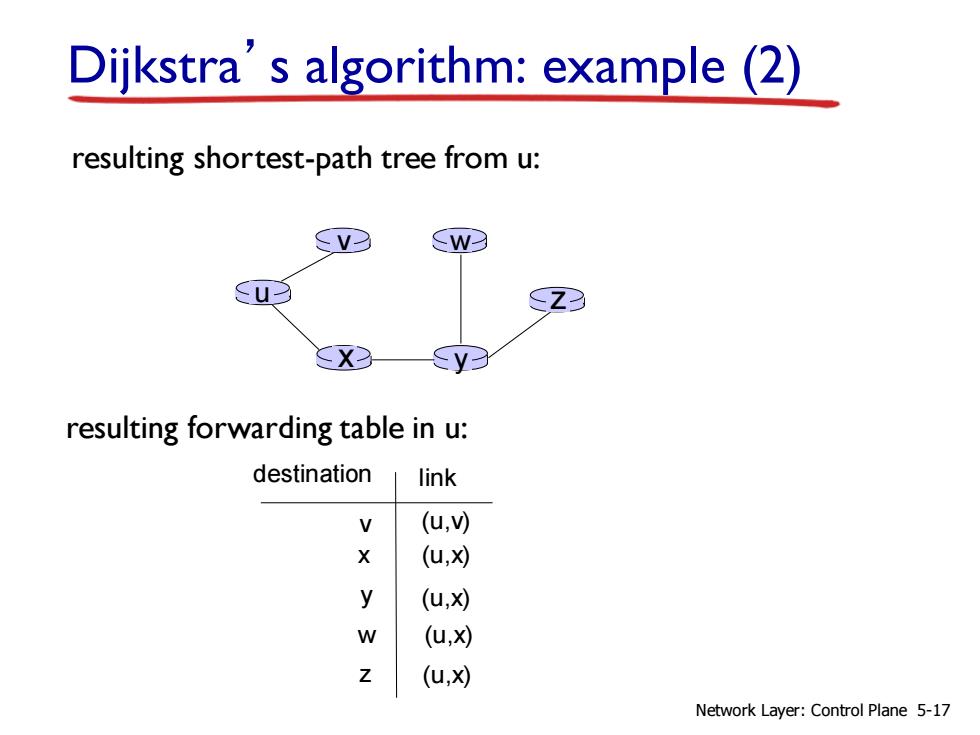
Dijkstra’s algorithm: example (2) u x y v w z resulting shortest-path tree from u: v x y w z (u,v) (u,x) (u,x) (u,x) (u,x) destination link resulting forwarding table in u: Network Layer: Control Plane 5-17
Dijkstra's algorithm,discussion algorithm complexity:n nodes each iteration:need to check all nodes,w,not in N n(n+1)/2 comparisons:O(n2) more efficient implementations possible:O(nlogn) oscillations possible: e.g.,support link cost equals amount of carried traffic: 2+e 十e e initially given these costs, given these costs, given these costs, find new routing.... find new routing....find new routing.... resulting in new costs resulting in new costs resulting in new costs Network Layer:Control Plane 5-18
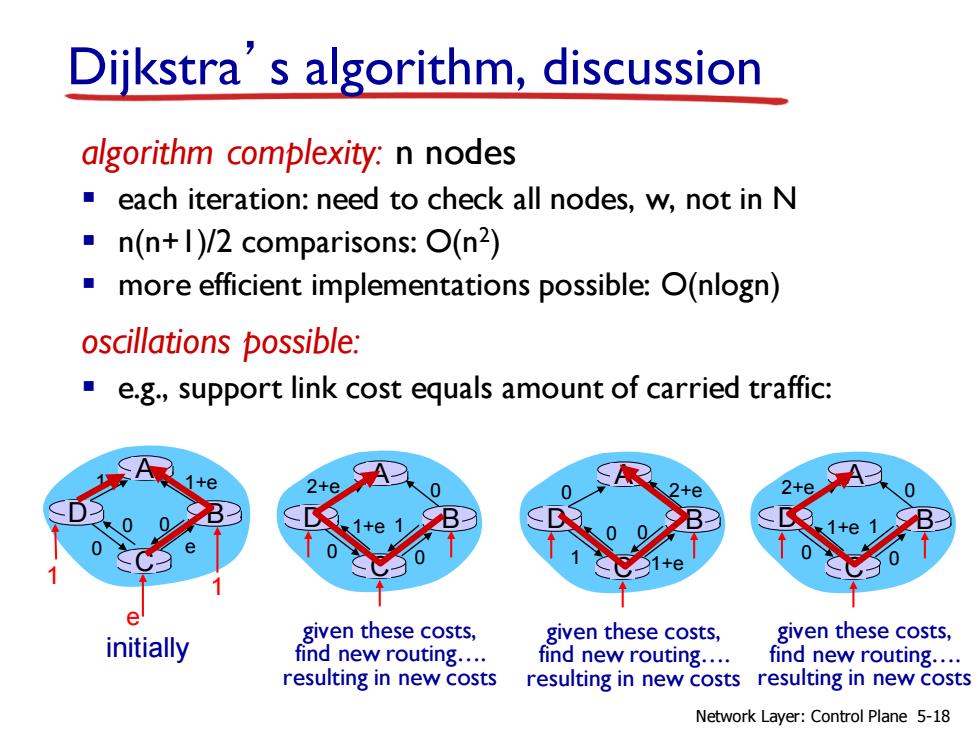
Dijkstra’s algorithm, discussion algorithm complexity: n nodes ▪ each iteration: need to check all nodes, w, not in N ▪ n(n+1)/2 comparisons: O(n2 ) ▪ more efficient implementations possible: O(nlogn) oscillations possible: ▪ e.g., support link cost equals amount of carried traffic: A D C B 1 1+e 0 e e 1 1 0 0 initially A D C B given these costs, find new routing…. resulting in new costs 2+e 0 0 0 1+e 1 A D C B given these costs, find new routing…. resulting in new costs 0 2+e 1+e 1 0 0 A D C B given these costs, find new routing…. resulting in new costs 2+e 0 0 0 1+e 1 Network Layer: Control Plane 5-18

Chapter 5:outline 5.I introduction 5.5 The SDN control plane 5.2 routing protocols 5.6 ICMP:The Internet ■link state Control Message ■distance vector Protocol 5.3 intra-AS routing in the 5.7 Network management Internet:OSPF and SNMP 5.4 routing among the ISPs: BGP Network Layer:Control Plane 5-19
5.1 introduction 5.2 routing protocols ▪ link state ▪ distance vector 5.3 intra-AS routing in the Internet: OSPF 5.4 routing among the ISPs: BGP 5.5 The SDN control plane 5.6 ICMP: The Internet Control Message Protocol 5.7 Network management and SNMP Chapter 5: outline Network Layer: Control Plane 5-19

Distance vector algorithm Bellman-Ford equation(dynamic programming) let d,(y):=cost of least-cost path from x to y then d,(y)=min {c(x,v)+d(y)} cost from neighbor v to destination y cost to neighbor v min taken over all neighbors v of x Network Layer:Control Plane 5-20
Distance vector algorithm Bellman-Ford equation (dynamic programming) let dx (y) := cost of least-cost path from x to y then dx (y) = min {c(x,v) + dv (y) } v cost to neighbor v min taken over all neighbors v of x cost from neighbor v to destination y Network Layer: Control Plane 5-20