
Decimal System ◆ The decimal system can be used to represent both the integer as well as floating point values.The floating point values are generally represented in this system by using a period called decimal point. ◆ The decimal point is used to separate the integer part and the fraction part of the given floating point number. The value of any number represented in the decimal system can be determined by first multiplying the weight associated with each digit in the given number with the digit itself and then adding all these values produced as a result of multiplication operation
Decimal System ◼ The decimal system can be used to represent both the integer as well as floating point values. The floating point values are generally represented in this system by using a period called decimal point. ◼ The decimal point is used to separate the integer part and the fraction part of the given floating point number. ◼ The value of any number represented in the decimal system can be determined by first multiplying the weight associated with each digit in the given number with the digit itself and then adding all these values produced as a result of multiplication operation
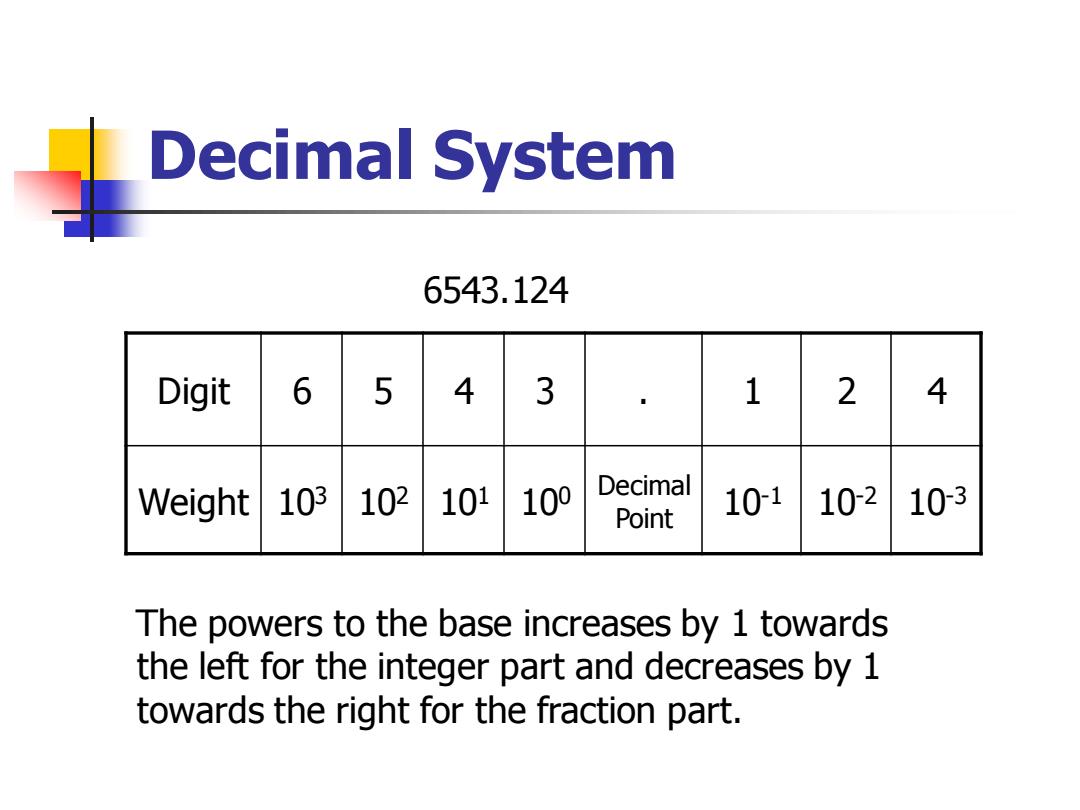
Decimal System 6543.124 Digit 6 5 43 1 2 4 Weight 103 102 101 100 Decimal Point 101 10-2 10-3 The powers to the base increases by 1 towards the left for the integer part and decreases by 1 towards the right for the fraction part
Decimal System Digit 6 5 4 3 . 1 2 4 Weight 103 102 101 100 Decimal Point 10-1 10-2 10-3 6543.124 The powers to the base increases by 1 towards the left for the integer part and decreases by 1 towards the right for the fraction part

Binary System The binary system uses base 2 to represent different values.Therefore,the binary system is also known as base-2 system. ■ As this system uses base 2,only two symbols are available for representing the different values in this system.These symbols are 0 and 1,which are also know as bits in computer terminology. 0 Using binary system,the computer systems can store and process each type of data in terms of 0s and 1s only
Binary System ◼ The binary system uses base 2 to represent different values. Therefore, the binary system is also known as base-2 system. ◼ As this system uses base 2, only two symbols are available for representing the different values in this system. These symbols are 0 and 1, which are also know as bits in computer terminology. ◼ Using binary system, the computer systems can store and process each type of data in terms of 0s and 1s only

Binary System The following are some of the technical terms used in binary system: o I Bit:It is the smallest unit of information used in a computer system.It can either have the value 0 or 1.Derived from the words anary dit/7. Nibble:It is a combination of 4 bits. Byte:It is a combination of 8 bits. ■ Word:It is a combination of 16 bits. Double word:It is a combination of 32 bits. Kilobyte(KB):It is used to represent the 1024 bytes of information. Megabyte(MB):It is used to represent the 1024 KBs of information. Gigabyte (GB):It is used to represent the 1024 MBs of information
Binary System The following are some of the technical terms used in binary system: ◼ Bit: It is the smallest unit of information used in a computer system. It can either have the value 0 or 1. Derived from the words Binary ditIT. ◼ Nibble: It is a combination of 4 bits. ◼ Byte: It is a combination of 8 bits. ◼ Word: It is a combination of 16 bits. ◼ Double word: It is a combination of 32 bits. ◼ Kilobyte (KB): It is used to represent the 1024 bytes of information. ◼ Megabyte (MB): It is used to represent the 1024 KBs of information. ◼ Gigabyte (GB): It is used to represent the 1024 MBs of information
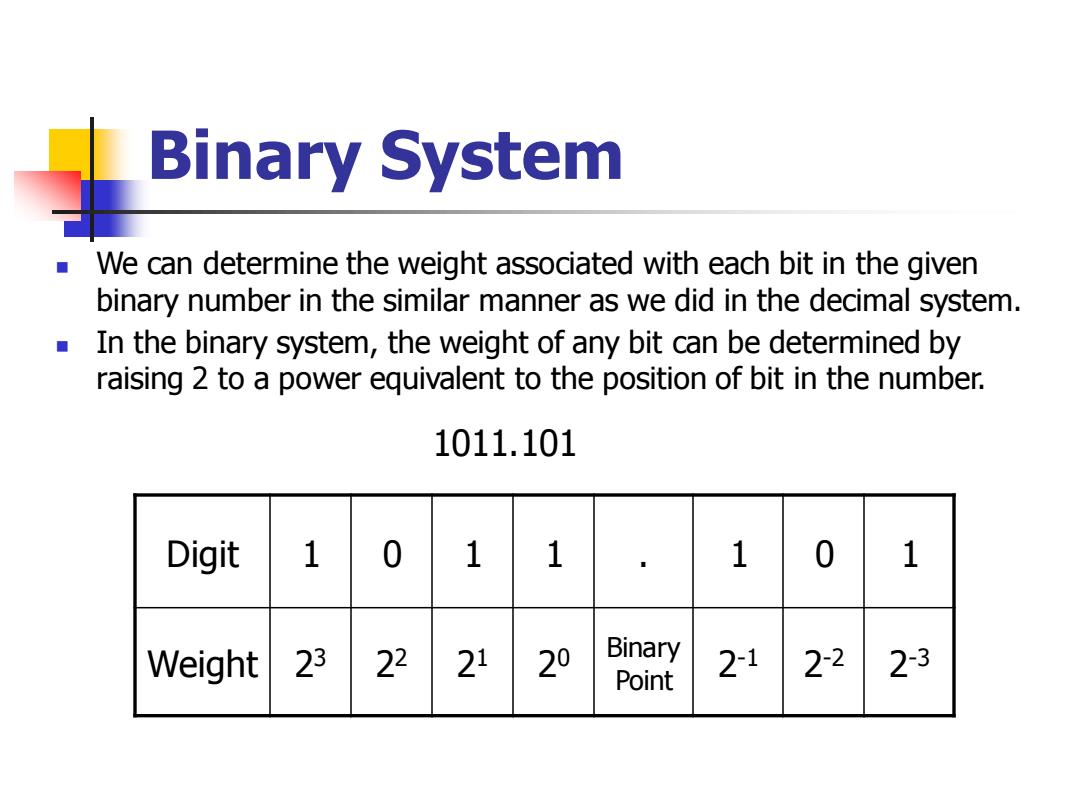
Binary System We can determine the weight associated with each bit in the given binary number in the similar manner as we did in the decimal system. In the binary system,the weight of any bit can be determined by raising 2 to a power equivalent to the position of bit in the number. 1011.101 Digit 1 0 1 1 1 0 1 Weight 23 22 21 20 Binary Point 21 22 2-3
Binary System ◼ We can determine the weight associated with each bit in the given binary number in the similar manner as we did in the decimal system. ◼ In the binary system, the weight of any bit can be determined by raising 2 to a power equivalent to the position of bit in the number. Digit 1 0 1 1 . 1 0 1 Weight 2 3 2 2 2 1 2 0 Binary Point 2 -1 2 -2 2 -3 1011.101