
d 体育运动会项目分组* pre(前一个出队列的元素序号)=n;组号=O; 全体元素入队列; while(队列不空){ 队首元素出对列; fi<pre){/需要开辟新的组 组号+;clash数组初始化; if可以入当前组){ i入组,记下i所属的组号;修改clash数组; else重新入队列; pre=i; ypb@ustc.edu.cn 16 中国科学技术大学
ypb@ustc.edu.cn 16 中国科学技术大学 体育运动会项目分组* pre(前一个出队列的元素序号)=n;组号=0; 全体元素入队列; while(队列不空){ 队首元素i出对列; if(i<pre){ //需要开辟新的组 组号++;clash数组初始化; } if(i可以入当前组){ i入组,记下i所属的组号;修改clash数组; } else i重新入队列; pre=i; }
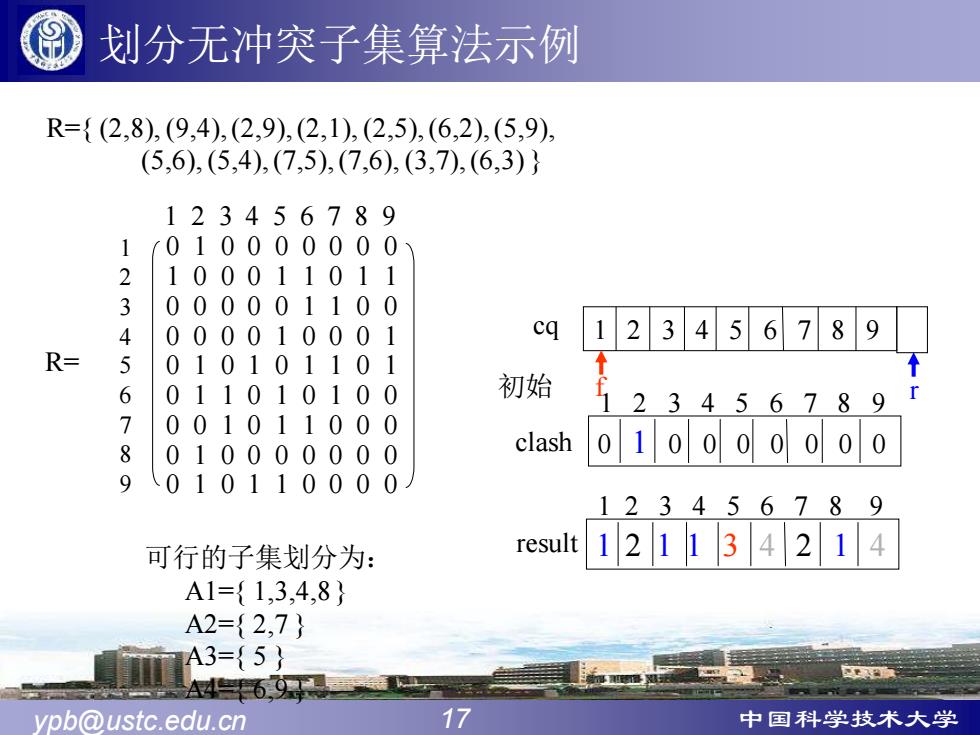
划分无冲突子集算法示例 R={(2,8),(9,4),(2,9),(2,1),(2,5),(6,2),(5,9), (5,6),(5,4),(7,5),(7,6),(3,7),(6,3)} 123456789 1 f010000000 2 100011011 3 000001100 4 000010001 cq 123456789 R= 5 010101101 6 011010100 初始 23456789 7 001011000 8 010000000 clash 010000000 9 010110000 123456789 可行的子集划分为: result 121134214 A1={1,3,4,8} A2={2,7} A3={5} 6, ypb@ustc.edu.cn 17 中国科学技术大学
ypb@ustc.edu.cn 17 中国科学技术大学 划分无冲突子集算法示例 0 1 0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 0 1 1 0 1 0 1 1 0 1 0 1 0 0 0 0 1 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 1 1 0 1 1 R= cq 1 2 3 4 5 6 7 8 9 初始 f r R={ (2,8), (9,4), (2,9), (2,1), (2,5), (6,2), (5,9), (5,6), (5,4), (7,5), (7,6), (3,7), (6,3) } 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 1 1 3 4 2 1 4 1 2 3 4 5 6 7 8 9 result 可行的子集划分为: A1={ 1,3,4,8 } A2={ 2,7 } A3={ 5 } A4={ 6,9 } 0 1 0 0 0 0 0 0 0 1 2 3 4 5 6 7 8 9 clash
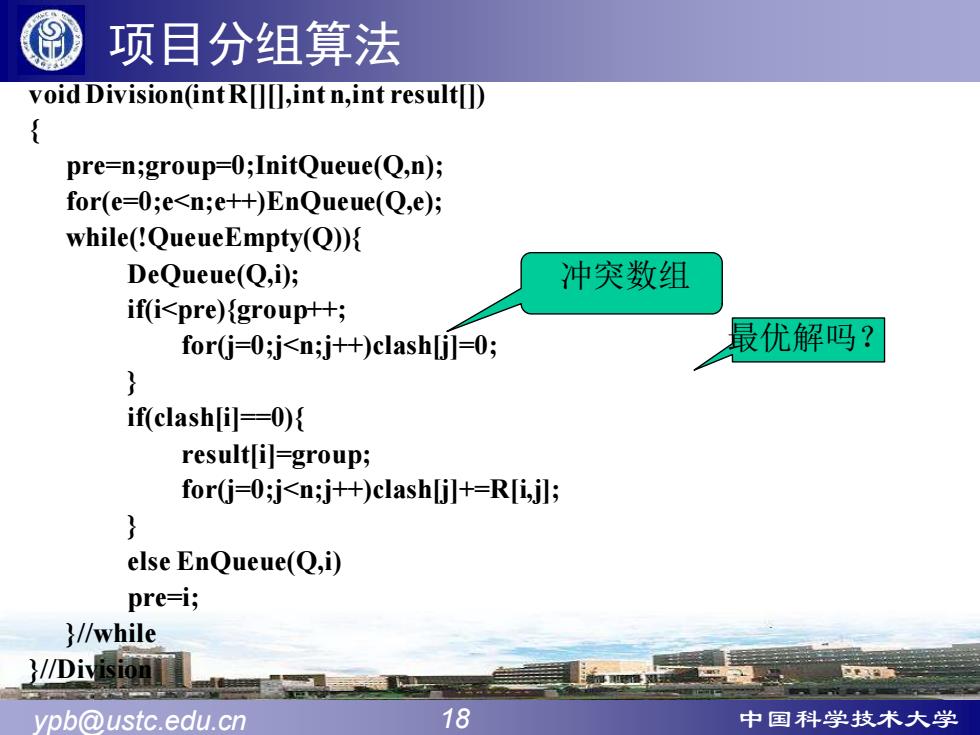
项目分组算法 void Division(int R[][,int n,int result[) pre-n;group-0;InitQueue(Q,n); for(e=0;e<n;e++)EnQueue(Q,e); while(:QueueEmpty(Q)){ DeQueue(Q,i); 冲突数组 ifi<pre){group叶+; for(j=0;j<n;j++)clash[jl=0; 最优解吗? if(clash[i]--0){ result[i]-group; for(j=0;j<n;j++)clash[j]+=R[i,jl; else EnQueue(Q,i) pre=i; }//while }//Division ypb@ustc.edu.cn 18 中国科学技术大学
ypb@ustc.edu.cn 18 中国科学技术大学 项目分组算法 void Division(intR[][],int n,int result[]) { pre=n;group=0;InitQueue(Q,n); for(e=0;e<n;e++)EnQueue(Q,e); while(!QueueEmpty(Q)){ DeQueue(Q,i); if(i<pre){group++; for(j=0;j<n;j++)clash[j]=0; } if(clash[i]==0){ result[i]=group; for(j=0;j<n;j++)clash[j]+=R[i,j]; } else EnQueue(Q,i) pre=i; }//while }//Division 冲突数组 最优解吗?

贪资心那 贪婪法,不是全局最优解 ypb@ustc.edu.cn 19 中国科学技术大学
ypb@ustc.edu.cn 19 中国科学技术大学 贪婪法,不是全局最优解

3.7递归应用示例 讨论以下经典问题: >Ackerman函数 >汉诺塔问题 >八皇后问题 >地图着色问题 ypb@ustc.edu.cn 20 中国科学技术大学
ypb@ustc.edu.cn 20 中国科学技术大学 讨论以下经典问题: ➢ Ackerman函数 ➢ 汉诺塔问题 ➢ 八皇后问题 ➢ 地图着色问题 3.7递归应用示例