
3.1.2.2中位数(Median) 中位数和众数一样,也是一种位置代表值。中位数是将总体中 的数据按顺序排列后,处于数列中点位置上的那个数据值或变量值 ,或者说中位数是累计频率数列中,累计频率为0.50所对应的变量 值。用Me表示。 在总体中,小于中位数的数据个数占一半,大于中位数的数据 个数也占一半,即中位数是将数据按大小顺序排列后,位于二等分 点上的那个数据值。用中位数来代表总体中所有标志值的一般水 平, 可以避免极端值的影响,在有些情况下更具有代表性。 中位数的确定方法,根据所掌握的数据不同而有所不同
3.1.2.2 中位数(Median) 中位数和众数一样,也是一种位置代表值。中位数是将总体中 的数据按顺序排列后,处于数列中点位置上的那个数据值或变量值 ,或者说中位数是累计频率数列中,累计频率为0.50所对应的变量 值。用Me表示。 在总体中,小于中位数的数据个数占一半,大于中位数的数据 个数也占一半,即中位数是将数据按大小顺序排列后,位于二等分 点上的那个数据值。用中位数来代表总体中所有标志值的一般水 平, 可以避免极端值的影响,在有些情况下更具有代表性。 中位数的确定方法,根据所掌握的数据不同而有所不同

[例3-4]某高校一次对食堂伙食满意度的调查 数据如表3-4所示。求满意度的中位数。 表3-4 调查数据次数分布 回答类别 学生人数(人) 学生人数累计(向上累计) 非常不满意 240 240 不满意 1080 1320 一 般 930 2250 满意 450 2700 非常满意 300 3000 合 计 3000 中位数位置=3000/2=1500 从学生数累计看,中位数在第三组,所以,Me= 般
[例3-4] 某高校一次对食堂伙食满意度的调查 数据如表 3-4所示。求满意度的中位数。 回答类别 学生人数(人) 学生人数累计(向上累计) 非常不满意 240 240 不满意 1 080 1 320 一 般 930 2 250 满 意 450 2 700 非常满意 300 3 000 合 计 3 000 —— 表3-4 调查数据次数分布 中位数位置 = 3 000/2 = 1 500 从学生数累计看,中位数在第三组,所以,Me = 一 般

3.1.2.2.2由单项式分组数量数据确定中位数 单项式数量数据分组已经将数据顺序化,这时数据个数即总体 单位数n=∑f,确定中位数位置的方法要通过累计次数计算。 [例3-6]由表3-5数据计算中位数。 中位数的位置是85/2=42.5,因此,Me=2。 表3-5 教师开课门数累计频数表 开课门数(门) 教师数(人) 向上累计教师数(人) 向下累计教师数(人) 15 15 85 2 30 45 70 3 28 73 40 4 12 85 12 合计 85
3.1.2.2.2 由单项式分组数量数据确定中位数 单项式数量数据分组已经将数据顺序化,这时数据个数即总体 单位数n=∑f,确定中位数位置的方法要通过累计次数计算。 [例3-6]由表3-5数据计算中位数。 中位数的位置是85/2 =42.5,因此,Me=2。 表3-5 教师开课门数累计频数表 开课门数(门) 教师数(人) 向上累计教师数(人) 向下累计教师数(人) 1 15 15 85 2 30 45 70 3 28 73 40 4 12 85 12 合计 85 —— ——
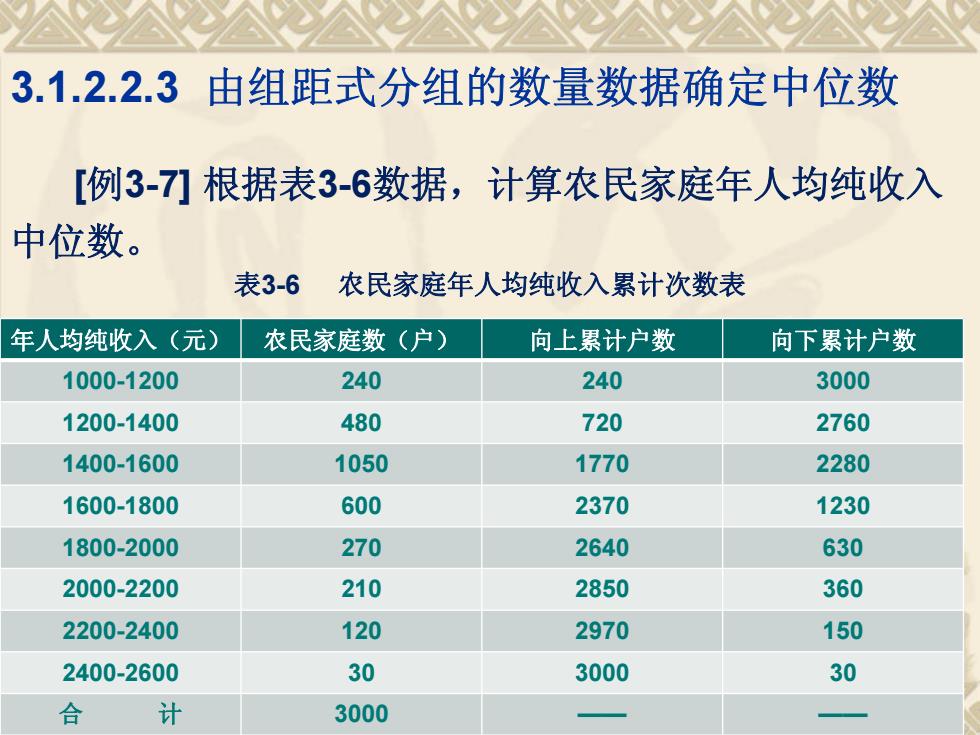
3.1.2.2.3由组距式分组的数量数据确定中位数 [例3-7]根据表3-6数据,计算农民家庭年人均纯收入 中位数。 表3-6 农民家庭年人均纯收入累计次数表 年人均纯收入(元) 农民家庭数(户) 向上累计户数 向下累计户数 1000-1200 240 240 3000 1200-1400 480 720 2760 1400-1600 1050 1770 2280 1600-1800 600 2370 1230 1800-2000 270 2640 630 2000-2200 210 2850 360 2200-2400 120 2970 150 2400-2600 30 3000 30 合 计 3000
3.1.2.2.3 由组距式分组的数量数据确定中位数 [例3-7] 根据表3-6数据,计算农民家庭年人均纯收入 中位数。 表3-6 农民家庭年人均纯收入累计次数表 年人均纯收入(元) 农民家庭数(户) 向上累计户数 向下累计户数 1000-1200 240 240 3000 1200-1400 480 720 2760 1400-1600 1050 1770 2280 1600-1800 600 2370 1230 1800-2000 270 2640 630 2000-2200 210 2850 360 2200-2400 120 2970 150 2400-2600 30 3000 30 合 计 3000 —— ——

3.1.2.3.1四分位数(Quartile) 四分位数又称为四分位点,它利用三个等分点将数据四等分: 第一个等分点称为下四分位数,第二个等分点就是中位数,第三个 等分点称为上四分位数。 四分位数的计算方法与中位数相似,即先确定其位置,再确定其 数值。 (1)顺序数据四分位数位置的确定 Q=in/4(ie1,2,3) 式中,Q是第i个四分位数,n是数据个数即总体单位数。 (2)未分组和单项式分组的数量数据四分位数位置的确定 Q=i(n+1)/4(i=1,2,3) (3)组距式分组数量数据中四分位数位置的确定
3.1.2.3.1 四分位数(Quartile) 四分位数又称为四分位点,它利用三个等分点将数据四等分: 第一个等分点称为下四分位数,第二个等分点就是中位数,第三个 等分点称为上四分位数。 四分位数的计算方法与中位数相似,即先确定其位置,再确定其 数值。 (1)顺序数据四分位数位置的确定 Qi =in/4(i=1,2,3) 式中,Qi 是第i个四分位数,n是数据个数即总体单位数。 (2)未分组和单项式分组的数量数据四分位数位置的确定 Qi =i(n+1)/4(i=1,2,3) (3)组距式分组数量数据中四分位数位置的确定