
procedure insert_child (P:node;E:elemtype); (This procedure is defined for constructing trees in a top-down manner. B A node containing element E will be created and it will be made the right-most child of node P*) procedure delete (var T:tree); B (This procedure deletes all the nodes of the tree T,and T will be made an empty tree.The tree T should not be a subtree of another tree * procedure assign(T1 tree;var T2:tree); (This procedure copies the entire tree T1 and asigns it to T2 * S/B 你能够从你的判断中得到一个一般 性的规律吗: 当你定义一个数据结构时,哪些操 作是必须的,哪些操作是特定的?
B B S/B 你能够从你的判断中得到一个一般 性的规律吗: 当你定义一个数据结构时,哪些操 作是必须的,哪些操作是特定的?

你有没有感觉到,在树这样的数据结构中,递 归如呼吸般自然? ways.These are known as tree walkings or tree traversals.In a tree with the root N and subtrees T1,T2,...,Tn we define: pre-order traversal:visit the root node N,then visit all the nodes in T in pre-order,then visit all the nodes in T2 in pre-order, and so on until all the nodes in Tn are visited in pre-order. post-order traversal:visit the nodes of T1,T2,...,Tn in post-order (in that order);then visit the root node
你有没有感觉到,在树这样的数据结构中,递 归如呼吸般自然?

根树: Level 0 Root Inner node O Leaf Level 1 O Branching node Level 2 Height=3 Level 3 如果任意结点最多有两个子结点,则该根树成为二叉 树binary tree),显然用指针实现链表的方法很容易 扩展到二叉树
根树: Root Inner node Branching node Leaf Level 0 Level 1 Level 2 Level 3 Height=3 如果任意结点最多有两个子结点, 则该根树成为二叉 树(binary tree), 显然用指针实现链表的方法很容易 扩展到二叉树
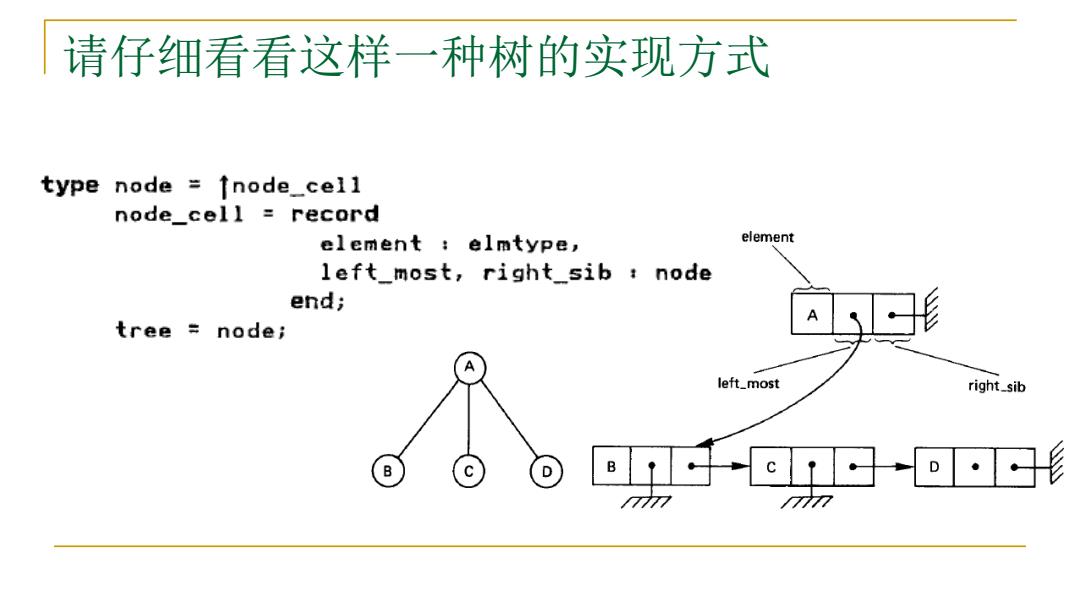
请仔细看看这样一种树的实现方式 type node÷1node_cei1 node_cel】=record element elmtype, element left_most,right_sib node end; tree node; □形 A left_most right_sib B ©□-o形 7777 777
请仔细看看这样一种树的实现方式

a C f 你能 还原 d 9 这颗 e h D 树吗? m
a b c d e g f h i j k mp n 你能 还原 这颗 树吗?