Dijkstra's algorithm:another example D D(w) D(x) D(Y) D(z) N 9 Step p(w p() p(y) p(Z) 0 7,u 3,U 5,u ∞ 5 1 w 6,W 5,00 11,W co 2 u 6,w 11,W 14,X Z 3 uwXv 10,V 14,X 4 12y 5 uwxvyz) notes: construct least-cost-path tree by tracing predecessor nodes ties can exist(can be broken arbitrarily) Network Layer:5-16
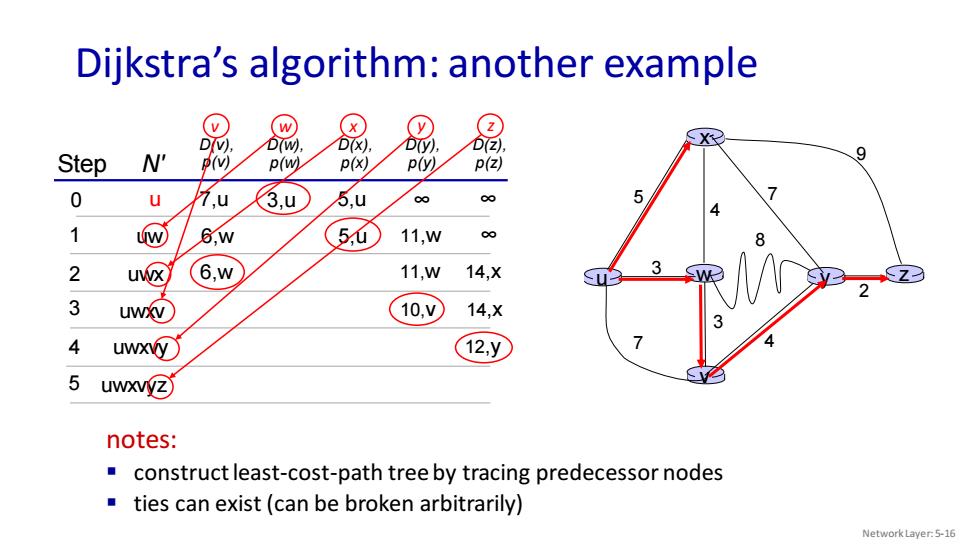
Dijkstra’s algorithm: another example Network Layer: 5-16 3 w 4 v x u 5 3 7 4 y 8 z 2 7 9 Step N' D(v), p(v) 0 1 2 3 4 5 D(w), p(w) D(x), p(x) D(y), p(y) D(z), p(z) u 7,u 3,u 5,u ∞ ∞ uw 6,w 5,u 11,w ∞ uwx 6,w 11,w 14,x uwxv 10,v 14,x uwxvy 12,y notes: ▪ construct least-cost-path tree by tracing predecessor nodes ▪ ties can exist (can be broken arbitrarily) uwxvyz v w x y z

Dijkstra's algorithm:discussion algorithm complexity:n nodes each of n iteration:need to check all nodes,w,not in N n(n+1)/2 comparisons:O(n2)complexity more efficient implementations possible:O(nlogn) message complexity: each router must broadcast its link state information to other n routers efficient(and interesting!)broadcast algorithms:O(n)link crossings to disseminate a broadcast message from one source each router's message crosses O(n)links:overall message complexity:O(n2) Network Layer:5-17
Dijkstra’s algorithm: discussion Network Layer: 5-17 algorithm complexity: n nodes ▪ each of n iteration: need to check all nodes, w, not in N ▪ n(n+1)/2 comparisons: O(n 2 ) complexity ▪ more efficient implementations possible: O(nlogn) message complexity: ▪ each router must broadcast its link state information to other n routers ▪ efficient (and interesting!) broadcast algorithms: O(n) link crossings to disseminate a broadcast message from one source ▪ each router’s message crosses O(n) links: overall message complexity: O(n 2 )

Dijkstra's algorithm:oscillations possible when link costs depend on traffic volume,route oscillations possible sample scenario: routing to destination a,traffic entering at d,c,e with rates 1,e(<1),1 link costs are directional,and volume-dependent given these costs, given these costs, given these costs, initially find new routing.... find new routing.... find new routing.... resulting in new costs resulting in new costs resulting in new costs Network Layer:5-18
Dijkstra’s algorithm: oscillations possible Network Layer: 5-18 ▪ when link costs depend on traffic volume, route oscillations possible a d c b 1 1+e 0 e e 1 1 0 0 initially a d c b given these costs, find new routing…. resulting in new costs 2+e 0 0 0 1+e 1 a d c b given these costs, find new routing…. resulting in new costs 0 2+e 1+e 1 0 0 a d c b given these costs, find new routing…. resulting in new costs 2+e 0 0 0 1+e 1 ▪ sample scenario: • routing to destination a, traffic entering at d, c, e with rates 1, e (<1), 1 • link costs are directional, and volume-dependent e 1 1 e 1 1 e 1 1

Network layer:"control plane"roadmap ■introduction routing protocols link state ■distance vector intra-ISP routing:OSPF routing among ISPs:BGP network management, ■SDN control plane configuration Internet Control Message ·SNMP Protocol ·NETCONF/YANG Network Layer:5-19
Network layer: “control plane” roadmap ▪ network management, configuration • SNMP • NETCONF/YANG ▪ introduction ▪ routing protocols ▪ link state ▪ distance vector ▪ intra-ISP routing: OSPF ▪ routing among ISPs: BGP ▪ SDN control plane ▪ Internet Control Message Protocol Network Layer: 5-19

Distance vector algorithm Based on Bellman-Ford(BF)equation(dynamic programming): Bellman-Ford equation Let D(y):cost of least-cost path from x to y. Then: Dx(y)=miny (cx.v+Dv(y)) v's estimated least-cost-path cost to y min taken over all neighbors v of x direct cost of link from x to v Network Layer:5-20
Based on Bellman-Ford (BF) equation (dynamic programming): Distance vector algorithm Network Layer: 5-20 Let Dx (y): cost of least-cost path from x to y. Then: Dx (y) = minv { cx,v + Dv (y) } Bellman-Ford equation min taken over all neighbors v of x v’s estimated least-cost-path cost to y direct cost of link from x to v