
反码表示法的特点: 1、负数的反码表示不太直观。 2、 0的反码有两组。 3、 异号加运算步骤较简单, 将最高位进位加到运算 结果的最低位。 例1:A=1101,B=-1001, C=0111, 求D=A+B,E=C+B ①[A]反=01101[B]反=10110, 因|A|>|B|,D>0 [A]反+[B]反=01101+10110=“1”00011, [D]反=00011+1=00100,D=0100 ②[C]反=00111,因|C|<|B|,E<0 [C]反+[B]反00111+10110=“0”11101,[E]反=11101, E=[E]反-2m+1+1=11101-100000+1=-0010
反码表示法的特点: 1、负数的反码表示不太直观。 2、 0的反码有两组。 3、异号加运算步骤较简单,将最高位进位加到运算 结果的最低位。 例1: A=1101, B=-1001,C=0111, 求D=A+B,E=C+B ① [A]反=01101 [B]反=10110, 因︱A︱>︱B︱,D > 0 [A]反+ [B]反= 01101+10110=“1”00011, [D]反=00011+1= 00100 , D=0100 。 ②[C]反=00111 ,因︱C︱<︱B︱,E < 0 [C]反+ [B]反= 00111+10110=“0”11101, [E]反= 11101, E = [E]反-2n+1 +1= 11101-100000 +1= -0010

3、负数的二进制补码[X门补 负整数补码表示方式:(反码加1) n位数值码各位取反加1再加最高位符号位《1”。 n十1位二进制补码值与真值X的关系: [X]补=2n+1+X,-2n≤X<0 例:4位二进制整数 X=-1101,[X]反=10010,[X]0=10011 负小数补码表示方式: (反码加2-n) n位数值码各位取反加2-n,整数位为符号位《1”。 补码值与真值X的关系: [X]补=2+X,-1≤X<0 [0]补=0.000..0 例:4位二进制小数 Y=-0.1101,[X]=1.0011
3、负数的二进制补码[X]补 负整数补码表示方式:(反码加1) n位数值码各位取反加1再加最高位符号位“1‖ 。 n+1位二进制补码值与真值X的关系: [X]补 = 2n+1 +X ,- 2n ≤ X < 0 例: 4位二进制整数 X = -1101, [X]反= 10010,[X]补= 10011 负小数补码表示方式: (反码加2-n ) n位数值码各位取反加2-n,整数位为符号位“1‖ 。 补码值与真值X的关系: [X]补 = 2 + X ,- 1 ≤ X < 0 [0]补 = 0.000……0 例: 4位二进制小数 Y= - 0.1101, [X]补= 1.0011

运用补码进行二进制整数减法运算: A-B=A+(-B)=A+X=D,A、B>0,X<0 运算结果:[A补+[X]补=A+2n+1+X=D+2n+1 运算后和的补码[D]补=[A]补+[X]补,与D的符号有关。 若A>B,D>0,[D]补=D 而加补码的运算和:D+2+1≥2n+1,第n+2位=1, 运算和略去进位2+1等于D的补码。 若A<B,D<0, [D]补=D+2m+1 而加补码的运算和:D+2+1<2n+1,第n+2位=0, 运算和等于D的补码。 所以,电路进行整数补码加运算后略去进位信号就 是和的补码
运用补码进行二进制整数减法运算: A-B=A+(-B)= A + X = D, A、B > 0,X < 0 运算结果:[A]补 +[X]补= A+ 2n+1 +X =D + 2n+1 运算后和的补码 [D]补= [A]补 +[X]补,与D的符号有关。 若 A > B ,D > 0, [D]补=D 而加补码的运算和:D + 2n+1 ≥ 2n+1 ,第n+2位=1, 运算和略去进位2n+1等于D的补码。 若A<B,D<0, [D]补 = D+2n+1 而加补码的运算和: D + 2n+1 < 2n+1 ,第n+2位=0, 运算和等于D的补码。 所以,电路进行整数补码加运算后略去进位信号就 是和的补码

补码表示法的特点: 1、负数的补码表示不直观,求取不方便。 2、 0的补码只有一组。 3、异号加运算步骤最简单,舍去最高位进位即可。 例1:A=1101,B=-1001,C=0111, 求D=A+B,E=C+B ①[A]补=01101[B]补=10111, 因|A|>|B|,所以D>0,[D]补=D [A]补+[B]补=01101+10111=“1”00100, [D]补=00100,D=0100 ②[C]补=00111,因|C|<|B|,所以E<0, [E]补=2m+1+E [C]补+[B]补=00111+10111=“0”11110 [E]补=11110,E=[E]补-2+1=11110-100000 =-0010
补码表示法的特点: 1、负数的补码表示不直观,求取不方便。 2、 0的补码只有一组。 3、异号加运算步骤最简单,舍去最高位进位即可。 例1: A=1101, B=-1001,C=0111, 求D=A+B,E=C+B ① [A]补=01101 [B]补=10111, 因︱A︱>︱B︱,所以 D > 0 , [D]补= D [A]补+ [B]补=01101+10111=“1”00100, [D]补= 00100,D=0100 ② [C]补=00111 ,因︱C︱<︱B︱,所以E < 0, [E]补= 2n+1 +E [C]补+ [B]补= 00111+10111=“0”11110 [E]补=11110, E = [E]补- 2n+1 =11110-100000 = -0010
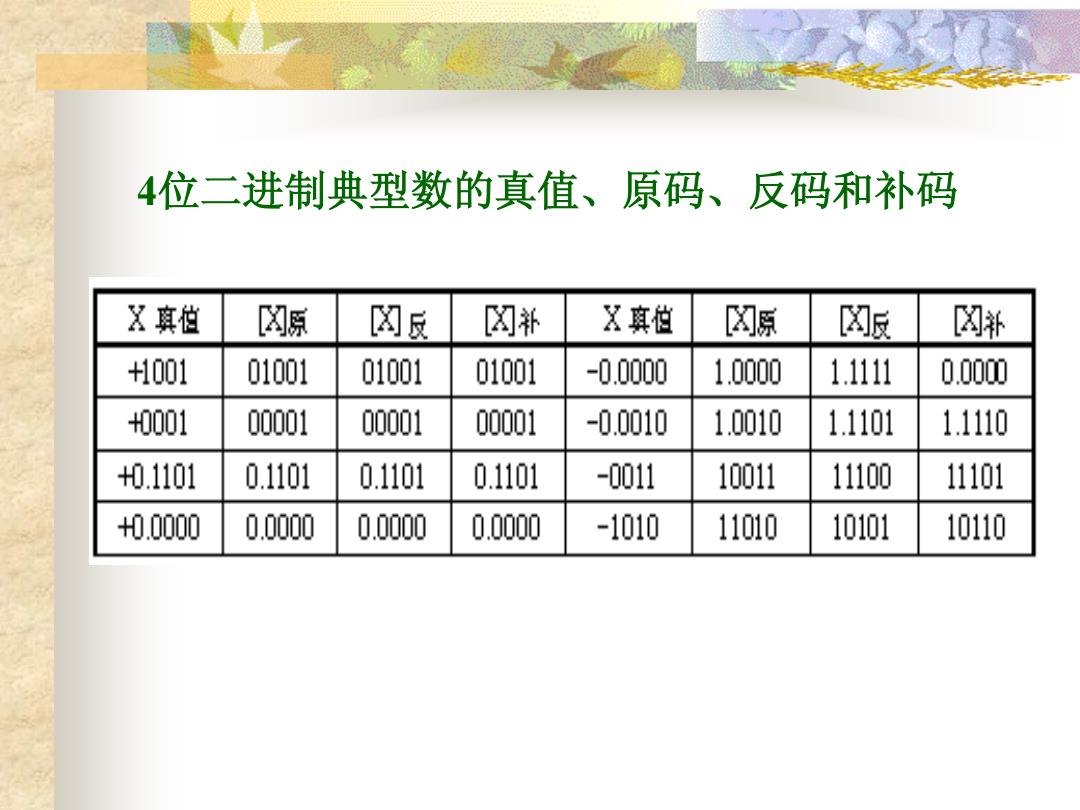
4位二进制典型数的真值、原码、反码和补码 X真位 ☒原 冈反 图补 X真但 ☒原 凶贩 ☒并 +1001 01001 01001 01001 -0.0000 1.0000 1.111 0.0000 +0001 00001 00001 00001 -0.0010 1.0010 1.1101 1.1110 +0.1101 0.1101 0.1101 0.1101 -0011 10011 11100 11101 +0.0000 0.0000 0.0000 0.0000 -1010 11010 10101 10110
4位二进制典型数的真值、原码、反码和补码