
Previous Works Motivation 上浒充通大 Main challenge and contribution SHANGHAI IIAO TONG UNIVERSITY The distribution of destination is analyzed for multicast scenario in social networks.Different from the unicast scenario in previous works,the investigated distribution is related with the multicast scale. The previous study of Euclidean Minimum Spanning Tree(EMST)is under the assumption that the node distribution is unrelated with the network scale.In this paper,a more general theorem is proposed for the case that the node distribution is related with the network scale,which further perfects the theory of EMST. The capacity upper-bound is calculated based on the EMST.An EMST-based transmission scheme is proposed,which is proved to achieve the capacity upper-bound of the social network. Finally,the impact of social features on network capacity is analyzed by comparing the social network capacity with traditional ad-hoc network. 11
Previous Works & Motivation Main challenge and contribution ➢ The distribution of destination is analyzed for multicast scenario in social networks. Different from the unicast scenario in previous works, the investigated distribution is related with the multicast scale. ➢ The previous study of Euclidean Minimum Spanning Tree (EMST) is under the assumption that the node distribution is unrelated with the network scale. In this paper, a more general theorem is proposed for the case that the node distribution is related with the network scale, which further perfects the theory of EMST. ➢ The capacity upper-bound is calculated based on the EMST. An EMST-based transmission scheme is proposed, which is proved to achieve the capacity upper-bound of the social network. ➢ Finally, the impact of social features on network capacity is analyzed by comparing the social network capacity with traditional ad-hoc network. 11

Outline 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY ▣Introduction System model and main idea The capacity upper-bound of multicast social networks OThe capacity achieving scheme ▣Discussion Conclusion and future directions 12
12 Outline ❑ Introduction ❑ System model and main idea ❑ The capacity upper-bound of multicast social networks ❑ The capacity achieving scheme ❑ Discussion ❑ Conclusion and future directions
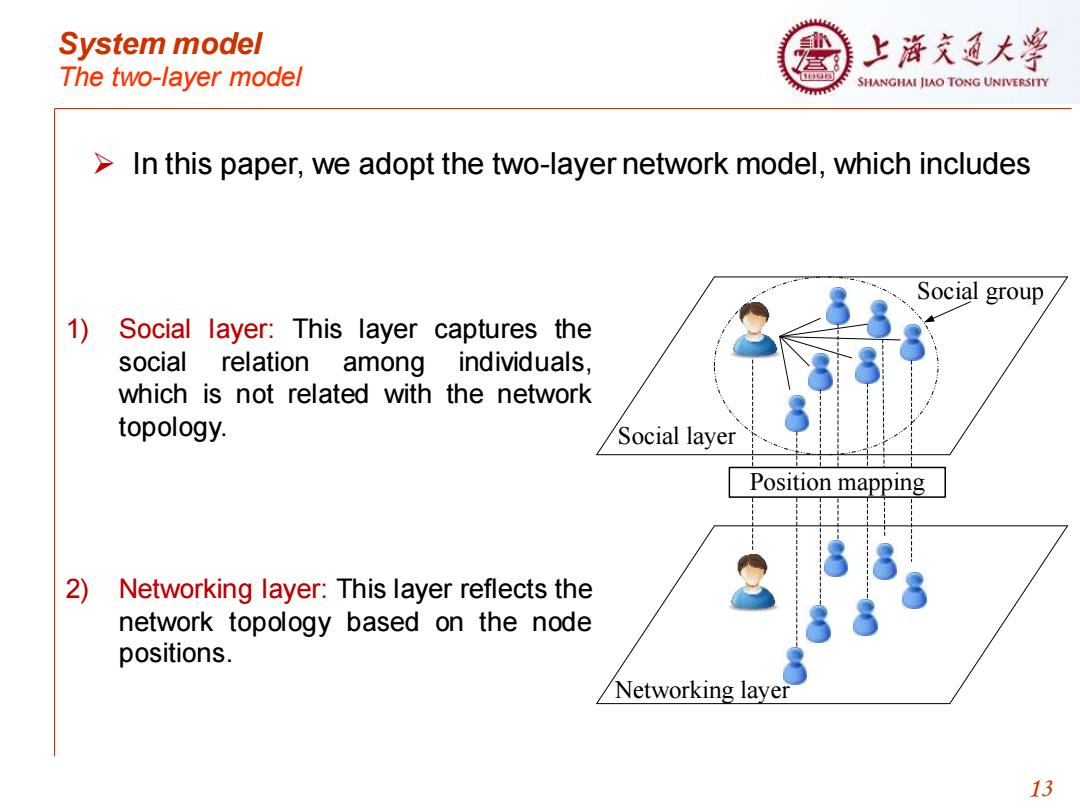
System model 上浒充通大 The two-layer model SHANGHAI JIAO TONG UNIVERSITY In this paper,we adopt the two-layer network model,which includes Social group 1) Social layer:This layer captures the social relation among individuals, which is not related with the network topology. Social layer Position mapping 2) Networking layer:This layer reflects the network topology based on the node positions. Networking layer 13
System model The two-layer model 13 ➢ In this paper, we adopt the two-layer network model, which includes 1) Social layer: This layer captures the social relation among individuals, which is not related with the network topology. 2) Networking layer: This layer reflects the network topology based on the node positions. Social group Social layer Networking layer Position mapping

System model 上浒充通大¥ The two-layer model SHANGHAI JIAO TONG UNIVERSITY Social layer For user i,the probability that it has g;friends satisfies Ptq.-qh-G.d 。1 where B>0 is a constant and G,is This model is verified by the study of large scale social networks [5][7] [81. Moreover,we assume that each user transmits information to all of its friends in this paper. 14
System model The two-layer model 14 ➢ Social layer For user i, the probability that it has qi friends satisfies 1 { } i n q q G q P = = where β>0 is a constant and Gn is 1 1 n n q G q = = This model is verified by the study of large scale social networks [5] [7] [8]. ✓ Moreover, we assume that each user transmits information to all of its friends in this paper

System model 上浒充通大¥ The two-layer model SHANGHAI JIAO TONG UNIVERSITY Networking layer Denoting P as the set consisting all the nodes and d(ij)as the distance between user i and /the rank of j with respect to i is defined as Rank,(j)=kEP:d(i,k)<d(i,j) For user i,the probability that user j is one of its g;friends satisfies 1 P=H,Rank(j) where a>0 is a constant and H,,is defined as This model is verified by the study of large scale social networks [10]. 15
System model The two-layer model 15 ➢ Networking layer For user i, the probability that user j is one of its qi friends satisfies Denoting P as the set consisting all the nodes and d(i,j) as the distance between user i and j, the rank of j with respect to i is defined as ( ) |{ : ( , ) ( , )}| Rank j k P d i k d i j i = 1 ( ) i j n i P H Rank j → = where α >0 is a constant and Hn is defined as 1 1 n n i H i = = This model is verified by the study of large scale social networks [10]