
电子斜技大学 软件技术基础 3.6.1图的基本概念 主讲教师:刘民岷 航空航天学院 a口2 软件技术基础课程组
软件技术基础 主讲教师:刘民岷 航空航天学院 软件技术基础课程组

图是一种对结点的前趋和后趋个数不加限制的数据结构, 在图结构中,结点之间的联系是任意的,每个结点都可以 与其它结点相联系。 有关图的理论,在“离散数学”的图论中有详细论述和证 明。在数据结构中,只讨论图在计算机中的实现和操作。 ·现实生活中,图的应用范围很广泛,涉及: 电讯工程、电网调度、集成电路设计 交通管理、工程管理、系统工程等领域 电子科技大学刘民岷 图 2
电子科技大学 刘民岷 图 2 • 图是一种对结点的前趋和后趋个数不加限制的数据结构, 在图结构中,结点之间的联系是任意的,每个结点都可以 与其它结点相联系。 • 有关图的理论,在“离散数学”的图论中有详细论述和证 明。在数据结构中,只讨论图在计算机中的实现和操作。 • 现实生活中,图的应用范围很广泛,涉及: – 电讯工程、电网调度、集成电路设计 – 交通管理、工程管理、系统工程等领域
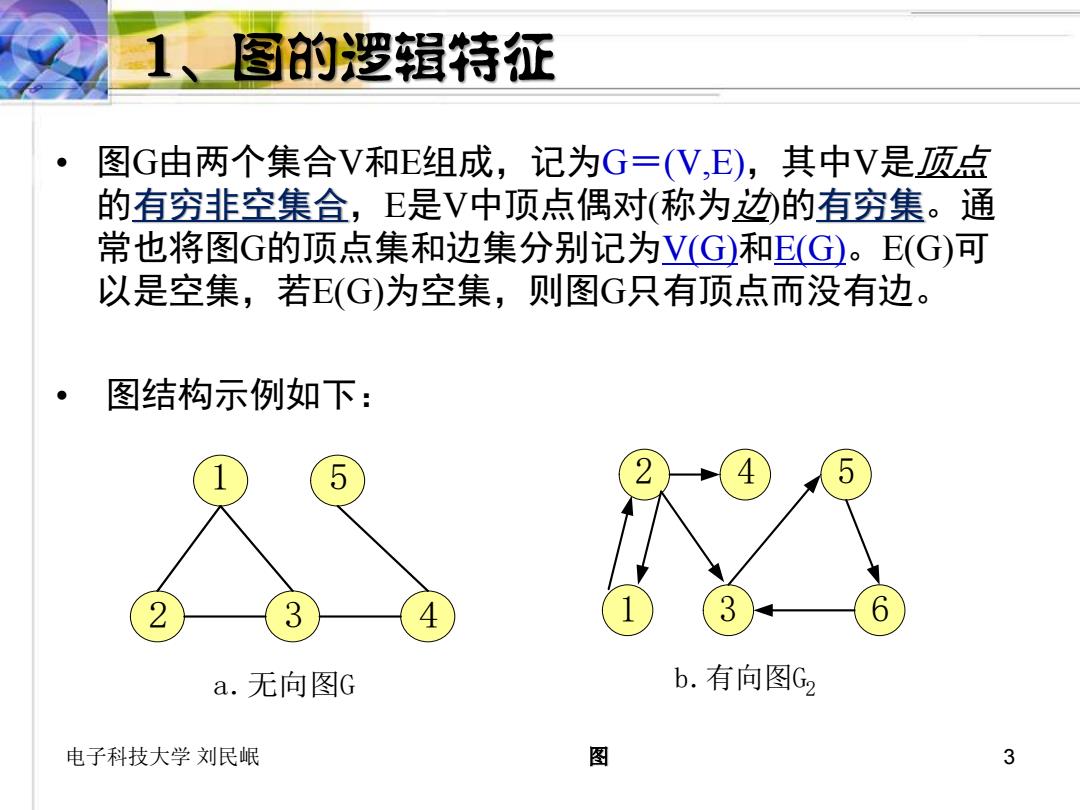
1、图的逻辑特征 图G由两个集合V和E组成,记为G=(V,E),其中V是顶点 的有穷非空集合,E是V中顶点偶对(称为边的有穷集。通 常也将图G的顶点集和边集分别记为V(G)和E(G)。E(G)可 以是空集,若E(G)为空集,则图G只有顶点而没有边。 图结构示例如下: 5 2 2 3 4 3 6 a.无向图G b.有向图G2 电子科技大学刘民岷 图 3
电子科技大学 刘民岷 图 3 • 图G由两个集合V和E组成,记为G=(V,E),其中V是顶点 的有穷非空集合,E是V中顶点偶对(称为边)的有穷集。通 常也将图G的顶点集和边集分别记为V(G)和E(G)。E(G)可 以是空集,若E(G)为空集,则图G只有顶点而没有边。 • 图结构示例如下: 1 2 3 4 5 a.无向图G 1 6 2 3 4 5 b.有向图G2
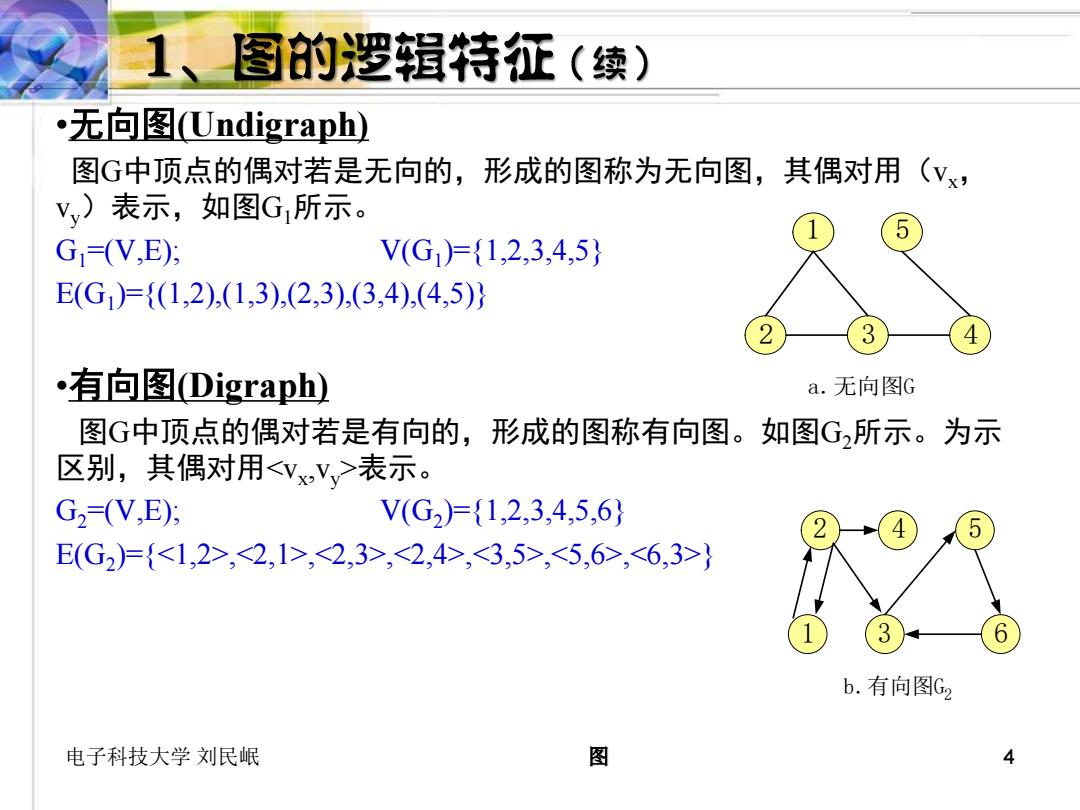
1、图的逻辑特征(续) 无▣图Undigraph) 图G中顶点的偶对若是无向的,形成的图称为无向图,其偶对用(Vx, Vv)表示,如图G所示。 G=(V,E); V(G1)={1,2,3,4,5} E(G1={(1,2),(1,3),(2,3),(3,4),(4,5)} 有向图Digraph) a.无向图G 图G中顶点的偶对若是有向的,形成的图称有向图。如图G,所示。为示 区别,其偶对用<Vx,Vy>表示。 G2(V,E): V(G2)={1,2,3,4,5,6} E(G2)={<1,2>,<2,1>,<2,3>,<2,4>,<3,5>,<5,6>,<6,3>} b.有向图G2 电子科技大学刘民岷 图 4
电子科技大学 刘民岷 图 4 •无向图(Undigraph) 图G中顶点的偶对若是无向的,形成的图称为无向图,其偶对用(vx, vy)表示,如图G1所示。 G1=(V,E); V(G1 )={1,2,3,4,5} E(G1 )={(1,2),(1,3),(2,3),(3,4),(4,5)} •有向图(Digraph) 图G中顶点的偶对若是有向的,形成的图称有向图。如图G2所示。为示 区别,其偶对用<vx ,vy >表示。 G2=(V,E); V(G2 )={1,2,3,4,5,6} E(G2 )={<1,2>,<2,1>,<2,3>,<2,4>,<3,5>,<5,6>,<6,3>} 1 2 3 4 5 a.无向图G 1 6 2 3 4 5 b.有向图G2

1、图的逻辑特征(续) 有关图结构的重要术语和概念 (I)邻接点:对于无向图,如果边(v,u)∈E,则v和u互为邻点,亦即u是v的邻 接点,v也是u的邻接点。 对于有向图,如果弧(v,u)∈E,则u是v的邻接点。 (2)顶点的度:常用D(V)表示,在无向图中,顶点的度就是以该顶点为一 个端点的边的条数。 在有向图中,以某顶点为弧头的弧的数目,称为此顶点的入度,常用 ID(V)表示;以某顶点为弧尾的弧的数目,常用OD(V)表示。有向图顶点 的度是此顶点的入度与出度之和,即D(V)=D(V)+OD(V)。 无论是有向图,还是无向图,顶点数n、边数e和度数之 间有如下关系: e=2) 电子科技大学刘民岷 图 5
电子科技大学 刘民岷 图 5 • 有关图结构的重要术语和概念 (1)邻接点:对于无向图,如果边(v,u)∈E,则v和u互为邻点, 亦即u是v的邻 接点,v也是u的邻接点。 对于有向图,如果弧(v,u)∈E,则u是v的邻接点。 (2)顶点的度:常用D(V)表示,在无向图中,顶点的度就是以该顶点为一 个端点的边的条数。 在有向图中,以某顶点为弧头的弧的数目,称为此顶点的入度,常用 ID(V)表示;以某顶点为弧尾的弧的数目,常用OD(V)表示。有向图顶点 的度是此顶点的入度与出度之和,即D(V)=ID(V)+OD(V)。 无论是有向图,还是无向图,顶点数n、边数e和度数之 间有如下关系: = = n i D Vi e 1 ( ) 2 1