
菲涅耳在惠更斯提出的子波假设基础上,补充 了描述次波基本特征的时空周期的物理量:位相和 振幅,及波的叠加。认为:从同一波阵面上各点发 出的次波,在传播过程中相遇时,也能相互叠加而 产生干涉现象,空间各点波的强度,由各子波在该 点的相干叠加所决定。这就是惠更斯一菲涅耳原理。 惠更斯—菲涅尔原理=次波与次波的相干叠加 首页上页下页退出
首 页 上 页 下 页 退 出 6 ❖ 菲涅耳在惠更斯提出的子波假设基础上,补充 了描述次波基本特征的时空周期的物理量:位相和 振幅,及波的叠加。认为:从同一波阵面上各点发 出的次波,在传播过程中相遇时,也能相互叠加而 产生干涉现象,空间各点波的强度,由各子波在该 点的相干叠加所决定。这就是惠更斯—菲涅耳原理。 惠更斯——菲涅尔原理= 次波与次波的相干叠加
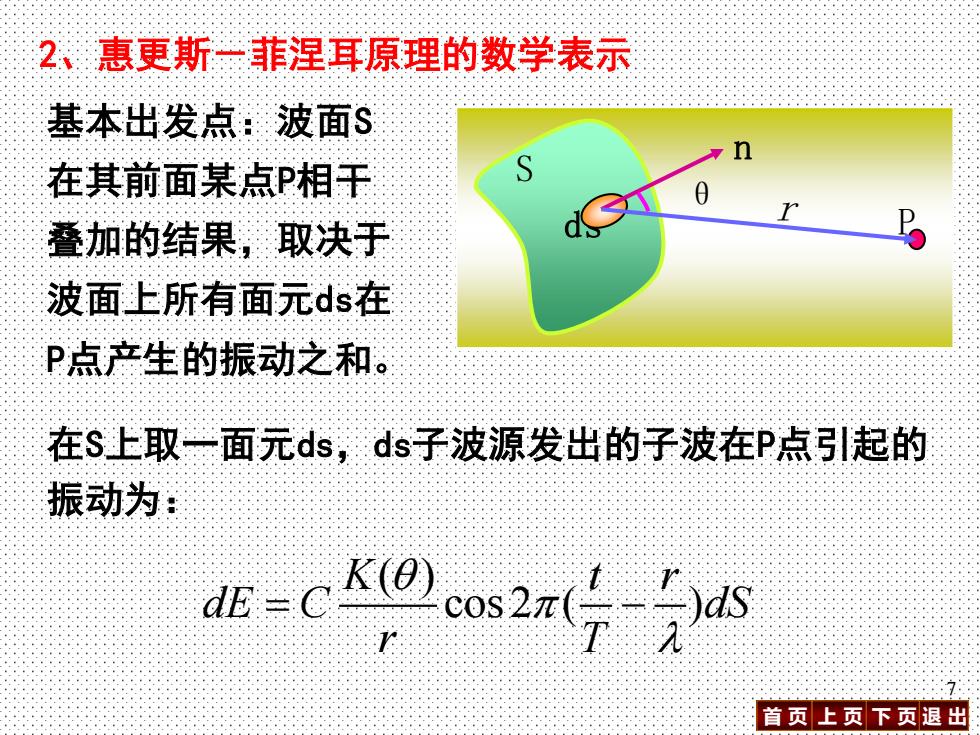
2、惠更斯一菲涅耳原理的数学表示 基本出发点:波面S 在其前面某点P相干 叠加的结果,取决于 波面上所有面元ds在 P点产生的振动之和。 在S上取一面元ds,ds子波源发出的子波在P点引起的 振动为: b=0as2r号26 首页上页下页退出
首 页 上 页 下 页 退 出 7 2、惠更斯-菲涅耳原理的数学表示 在S上取一面元ds,ds子波源发出的子波在P点引起的 振动为: ( ) cos 2 ( ) K t r dE C dS r T = − 基本出发点:波面S 在其前面某点P相干 叠加的结果,取决于 波面上所有面元ds在 P点产生的振动之和。 ds n S P θ r

式中C为比例系数,K(日)为随6角增大而缓慢减小 的函数,称为倾斜因子.当日=O时,K(θ)为最大; 当 时买K(9)=O,因而子波叠加后振幅为零 波阵面上所有6面元发出的子波在P点引起的 合振动为 6jak-co2ah 首页上页下页退出
首 页 上 页 下 页 退 出 8 ❖ 波阵面上所有dS面元发出的子波在P点引起的 合振动为 ( ) cos 2 ( ) K t r E dE C dS r T = = − 式中C为比例系数,K(θ)为随θ角增大而缓慢减小 的函数,称为倾斜因子.当θ=0时,K(θ)为最大; 当 时,K(θ)=0,因而子波叠加后振幅为零. 2
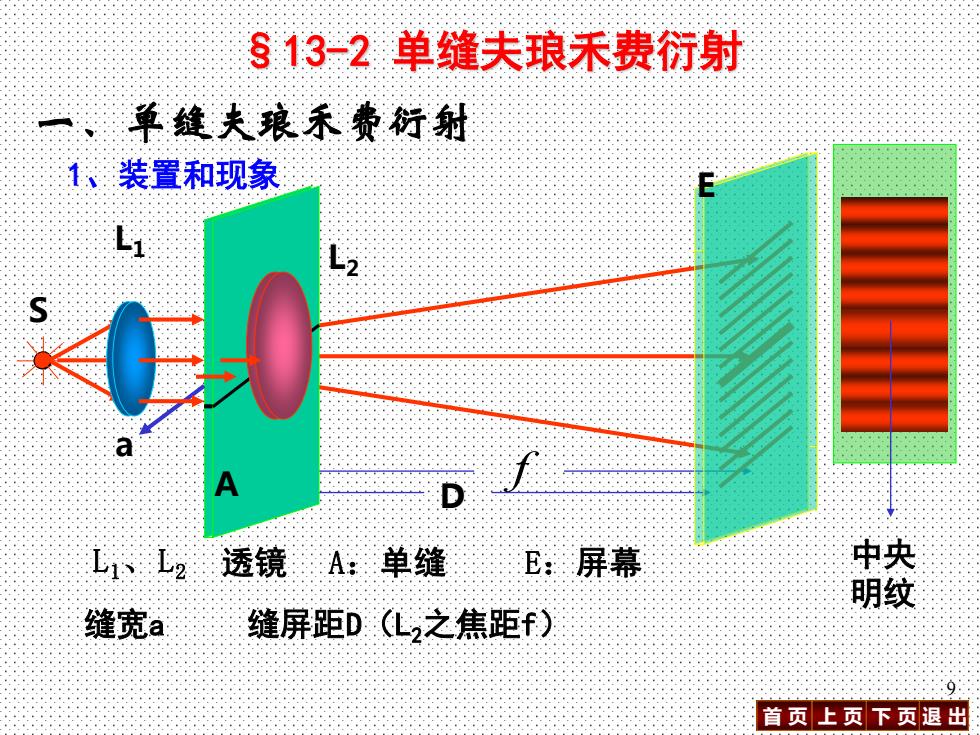
§13-2单缝夫琅禾费衍射 一、单缝夫琅禾费衍射 1、装置和现象 L 0 L1、L2透镜A:单缝E:屏幕 瑚胶 缝宽a 缝屏距D(L2之焦距f) 9 首页上页下页退出
首 页 上 页 下 页 退 出 9 §13-2 单缝夫琅禾费衍射 D f S 一、单缝夫琅禾费衍射 1、装置和现象 L1 A E L1、L2 透镜 A:单缝 E:屏幕 a 中央 明纹 L2 缝宽a 缝屏距D(L2之焦距f)

夫朗禾费单缝衍射图样是一组与狭缝平行的明暗相间的 条纹,其中中央条纹最亮最宽。 10 首页上页下页退出
首 页 上 页 下 页 退 出 10 夫朗禾费单缝衍射图样是一组与狭缝平行的明暗相间的 条纹,其中中央条纹最亮最宽