
Limit mesh approximation 口Limit mesh:push the control points to their limit positions. It inscribes the limit surface 口An interior mesh face F→a limit face F→a surface patch S We derive a bound on the distance between a patch S and its limit face F(or limit mesh)as max S(u,v)-F(u,v)<B(n)M (u.)e B(n)<C(n)means that the limit mesh approximates a CCSS better than the control mesh
Limit mesh approximation An interior mesh face → a limit face → a surface patch We derive a bound on the distance between a patch and its limit face (or limit mesh) as ◼ means that the limit mesh approximates a CCSS better than the control mesh F F S Limit mesh : push the control points to their limit positions. It inscribes the limit surface ( ) ( ) n C n S F ( , ) max ( , ) ( , ) ( ) u v u v u v n M S F−
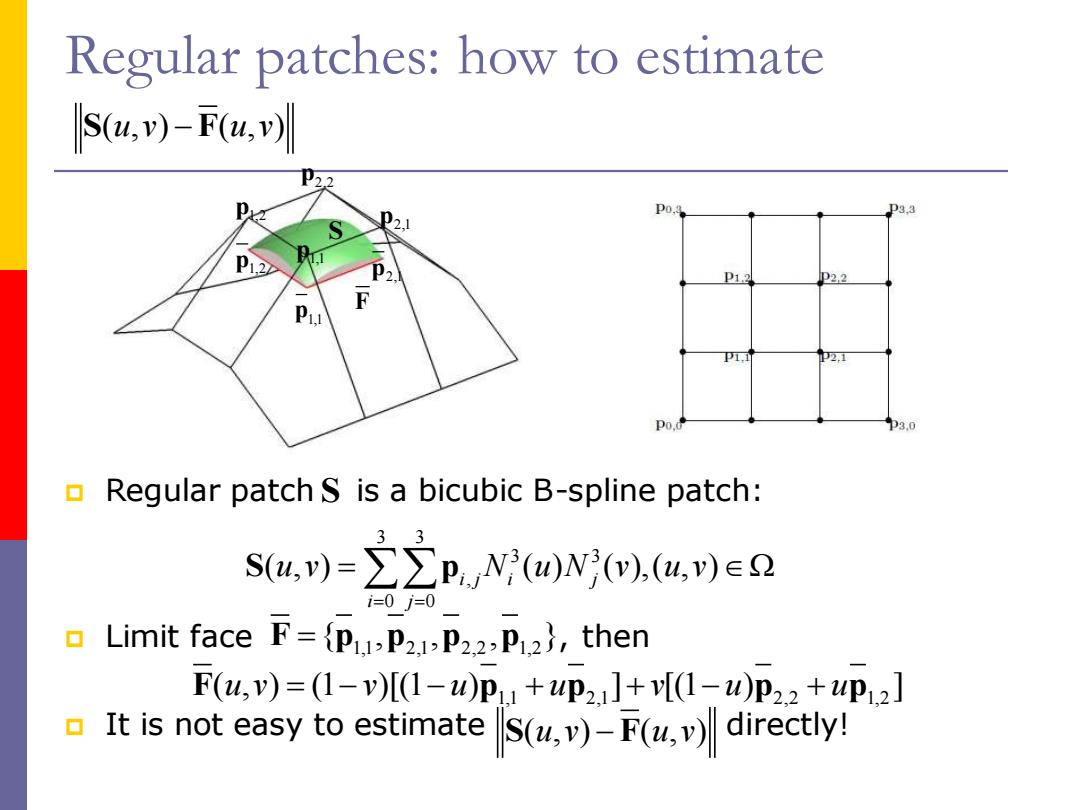
Regular patches:how to estimate S(4,y)-F(u,v) D. P2. P12 Regular patch S is a bicubic B-spline patch: Su,)=∑∑pN(0)w(,(u,)e2 1=0j-0 Limit face F={PuP2P22,P2),then F(,)=(1-v)[(1-)p+up2]+v[1-0)P22+up12] It is not easy to estimate S(u,v)-F(u,v)directly!
Regular patches: how to estimate Regular patch is a bicubic B-spline patch: Limit face , then It is not easy to estimate directly! S 3 3 3 3 , 0 0 ( , ) ( ) ( ), ( , ) i j i j i j u v N u N v u v = = S p = S F ( , ) ( , ) u v u v − 1,1 2,1 2,2 1,2 F p p p p ={ , , , } 1,1 2,1 2,2 1,2 F p p p p ( , ) (1 )[(1 ) ] [(1 ) ] u v v u u v u u = − − + + − + S F ( , ) ( , ) u v u v − S F p1,1 p1,2 p2,1 p2,2 p1,1 p2,1 p1,2