
例如对小自鼠从出生后第六天起,每隔三天称一次体 重,一直称到第18天,数据如表: 日龄(天)X6 912 15 18 体重(克)Y1217222529 试估计出生后第10天的体重?第17天的体重?所估计 体重的可靠程度是多少?
例如对小白鼠从出生后第六天起,每隔三天称一次体 例如对小白鼠从出生后第六天起,每隔三天称一次体 重,一直称到第 重,一直称到第 18天,数据如表: 天,数据如表: 日龄(天)X 6 9 12 15 18 X 6 9 12 15 18 体重(克)Y 12 17 22 25 29 Y 12 17 22 25 29 试估计出生后第 试估计出生后第10天的体重?第17天的体重?所估计 天的体重?所估计 体重的可靠程度是多少? 体重的可靠程度是多少?
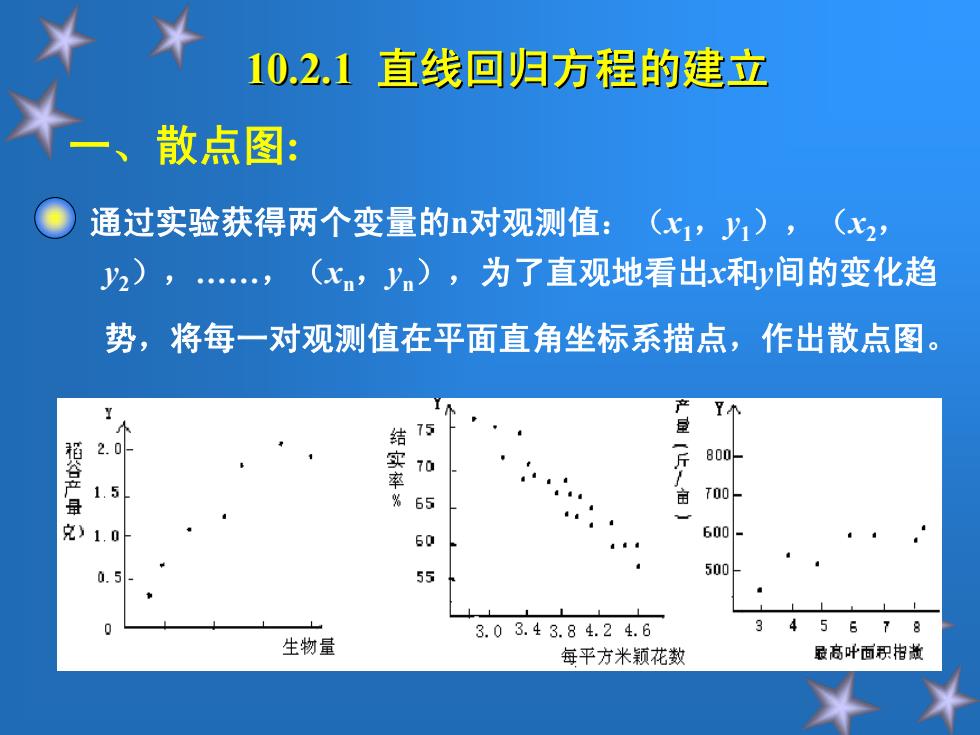
10.2.1直线回归方程的建立 散点图: 通过实验获得两个变量的n对观测值:( 1,y1),(2 (化,y),为了直观地看出x和y间的变化趋 势,将每一对观测值在平面直角坐标系描点,作出散点图。 产 75 2.0 稻谷产量 结实率% 斤 800 70 .5 65 T00 ) 1.0 a 600 0.5 55 500 3.03.43.84.24.6 4 5678 生物量 每平方米颖花数 最高叶面积相数
一、散点图: 通过实验获得两个变量的n对观测值:(x1,y1),(x2, y2),.,(xn,yn),为了直观地看出x和y间的变化趋 势,将每一对观测值在平面直角坐标系描点,作出散点图。 10.2.1 10.2.1 直线回归方程的建立 直线回归方程的建立

从散点图可以看出: ①两个变量间有关或无关;若有关两个变量间的关 系类型,是直线型还是曲线型; ②两个变量间直线关系的性质和相关程度; 散点图直观地、定性地表示了两个变量之间的关系。 为了探讨它们之间的规律性,还必须根据观测值将 其内在关系定量地表达出来
从散点图可以看出: 从散点图可以看出: ①两个变量间有关或无关 ①两个变量间有关或无关 ;若有关两个变量间的关 若有关两个变量间的关 系类型,是直线型还是曲线型; 系类型,是直线型还是曲线型; ②两个变量间直线关系的性质和相关程度; ②两个变量间直线关系的性质和相关程度; 散点图直观地、定性地表示了两个变量之间的关系。 表示了两个变量之间的关系。 为了探讨它们之间的规律性,还必须根据观测值将 为了探讨它们之间的规律性,还必须根据观测值将 其内在关系定量地表达出来

根据回归的定义: 1,X的每一个取值都有Y的一个正态分布与之对应。 2.为了描述X与Y间的数量关系,必须找出一个能代表Y 的值与x,对应,这个代表值只能是当X=x 时,Y的平均数4yx=x 3. Ly.x=x 称为Y的条件平均数 如何估计4yx= 是直线回归所要解决的问题
• 根据回归的定义: 1. X 的每一个取值都有 的每一个取值都有Y的一个正态分布与之对应。 的一个正态分布与之对应。 2. 为了描述X与Y间的数量关系,必须找出一个能代表 间的数量关系,必须找出一个能代表Y 的值与 对应,这个代表值只能是当 对应,这个代表值只能是当 时,Y的平均数 。 3. 3. 称为Y的条件平均数 i x i xX i .XY x i .XY x 如何估计 .XY xi 是直线回归所要解决的问题。 是直线回归所要解决的问题

二、直线回归的数学模型 1.借用y=a+bx, 2.得4yx=C+x 表示X的每一个取值都有一个Y的分布与之对 应,4yX=x Y~N(a+Bx,o2)
1. 借用 y=a+bx, 2. 得 , 表示 X 的每一个取值都有一个 Y 的分布与之对 应, x .XY ),(~ 2 xNY 二、直线回归的数学模型 二、直线回归的数学模型 XY xi