
The Mean Trick (for Variance Reduction) Variance and covariance: Var[X]=E[(X-E[X])2]=E[X2]-(EX])2 Cov(X,Y)=E (-E[X])(Y-E[Y]) ·Useful properties: Var[X a]Var[X] Var[ax]=a-Var[X] var[2冈2vami图+cmxx刘 诗判 For pairwise independent identically distributed X's: v2-立m灯-ow1
The Mean Trick (for Variance Reduction) • Variance and covariance: • Useful properties: Var[X] = 𝔼[(X − 𝔼[X]) 2 ] = 𝔼[X2 ] − (𝔼[X]) 2 Cov(X, Y) = 𝔼 [(X − 𝔼[X])(Y − 𝔼[Y])] Var[X + a] = Var[X] Var[aX] = a2 Var[X] Var [∑ i Xi ] = ∑ i Var[Xi ] + ∑ i≠j Cov(Xi , Xj ) • For pairwise independent identically distributed X ’s: i Var [ 1 k k ∑ i=1 Xi ] = 1 k2 k ∑ i=1 Var[Xi ] = 1 k Var[X1]

Input:a sequencex,...,U=[N] Output:an estimation of z= uniform independent hash functions ,...,[0,1] Min Sketch: for each1≤j≤k,lety=minh,(x: 1≤isn n2=方-1wne7= j=1 ·For every1≤j≤k: linearity of 以本 expectation 网=本 1 Var[Y≤ independence (z+1)2 Var[]≤ k(2+1)2
• uniform & independent hash functions h1,…, hk : U → [0,1] Min Sketch: for each , let ; return where ; 1 ≤ j ≤ k Yj = min 1≤i≤n hj (xi ) Z ̂ = 1 Y − 1 Y = 1 k k ∑ j=1 Yj 𝔼 [Yj] = 1 z + 1 Var[Yj ] ≤ 1 (z + 1)2 • For every 1 ≤ j ≤ k: 𝔼 [Y] = 1 z + 1 Var [Y] ≤ 1 k(z + 1)2 linearity of expectation independence Input: a sequence Output: an estimation of x1, x2,…, xn ∈ U = [N] z = {x1, x2, …, xn}
Input:a sequencex,..,U=[N] Output:an estimation of= {1,,x uniform independent hash functions ,...,U[0,1] Min Sketch: for each1≤j≤k,lety=minh,(x E[]= l≤isn z+1 k j=1 Var[冈≤ka+1可 。Goa:Pr E<(1-ekor2>1+e3 ≤6 assuming e≤1/2 4 Set k e26 -p> Pr 4 ≤6 (Chebyshev)
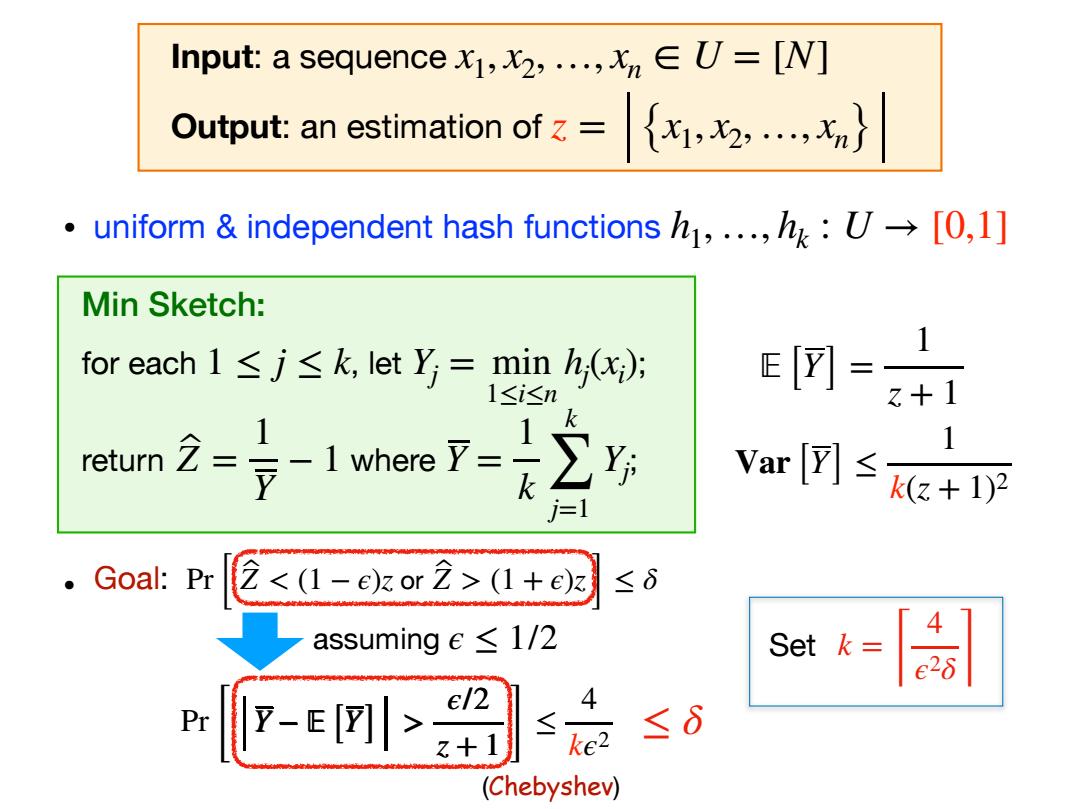
Y − 𝔼 [Y] > ϵ/2 z + 1 Pr [ Y − 𝔼 [Y] > ϵ/2 z + 1 ] ≤ 4 kϵ2 • Goal: Pr [ Z ̂ < (1 − ϵ)z or Z ̂ > (1 + ϵ)z ] ≤ δ assuming ϵ ≤ 1/2 (Chebyshev) k = ⌈ 4 ϵ2δ ⌉ Set ≤ δ • uniform & independent hash functions h1,…, hk : U → [0,1] Min Sketch: for each , let ; return where ; 1 ≤ j ≤ k Yj = min 1≤i≤n hj (xi ) Z ̂ = 1 Y − 1 Y = 1 k k ∑ j=1 Yj 𝔼 [Y] = 1 z + 1 Var [Y] ≤ 1 k(z + 1)2 Input: a sequence Output: an estimation of x1, x2,…, xn ∈ U = [N] z = {x1, x2, …, xn}
Input:a sequencex,..,=[N] Output:an estimation of z= ·uniform&independent hash functions h1,,hk:U→[0,l] Min Sketch:set k =[4/(e25)] for each1≤j≤k,lety=minh(x) 1≤i≤n wm=方-1wne-=2 1 Pr[1-ez≤2≤1+ek]≥1-6 .Space cost:) real numbers in [0,1] Storing k idealized hash functions
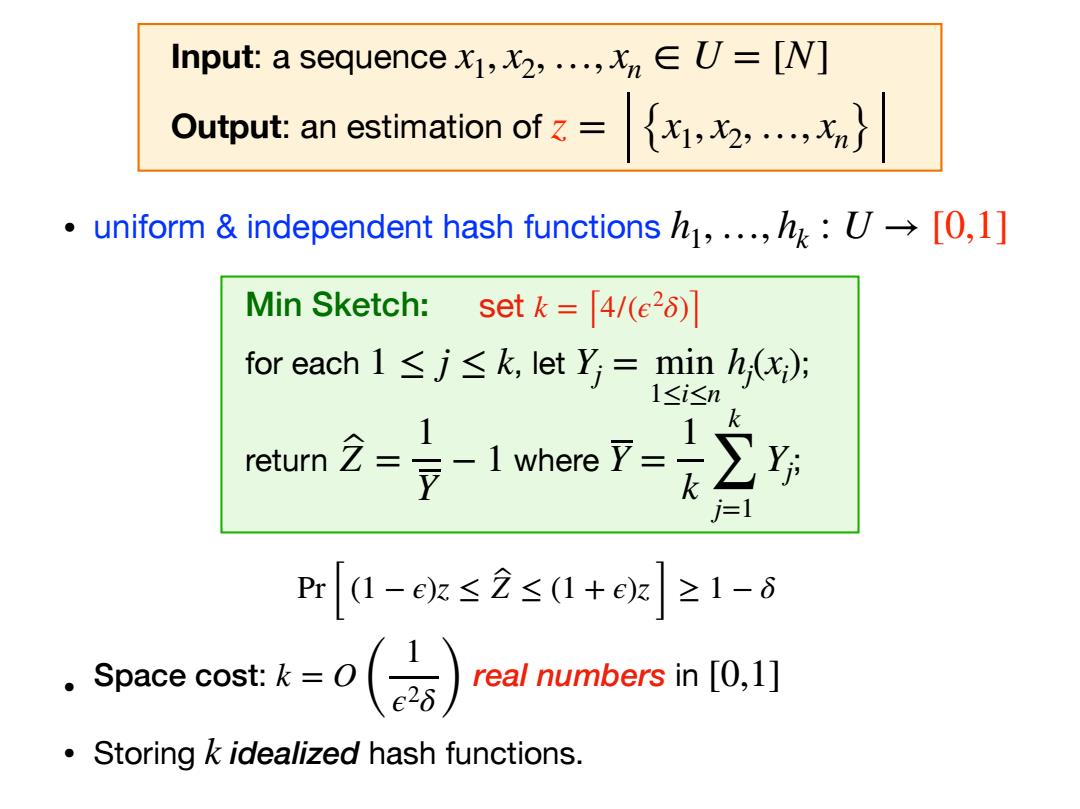
Min Sketch: for each , let ; return where ; 1 ≤ j ≤ k Yj = min 1≤i≤n hj (xi ) Z ̂ = 1 Y − 1 Y = 1 k k ∑ j=1 Yj • Space cost: real numbers in • Storing idealized hash functions. k = O ( 1 ϵ2δ) [0,1] k Pr [ (1 − ϵ)z ≤ Z ̂ ≤ (1 + ϵ)z ] ≥ 1 − δ set k = ⌈4/(ϵ2 δ)⌉ • uniform & independent hash functions h1,…, hk : U → [0,1] Input: a sequence Output: an estimation of x1, x2,…, xn ∈ U = [N] z = {x1, x2, …, xn}

Universal Hashing Universal Hash Family(Carter and Wegman 1979): A family of hash functions in -[m]is k-universal if for any distinct,...,U, Pr[h(c)=…=h()]≤ h∈t Moreover,is strongly k-universal(k-wise independent) if for any distinctx,..,Uand any y1,...,y[m], 八=小 1
Universal Hashing Universal Hash Family (Carter and Wegman 1979): A family of hash functions in is -universal if for any distinct , . Moreover, is strongly -universal ( -wise independent) if for any distinct and any , . ℋ U → [m] k x1, …, xk ∈ U Pr h∈ℋ [ h(x1) = ⋯ = h(xk)] ≤ 1 mk−1 ℋ k k x1, …, xk ∈ U y1, …, yk ∈ [m] Pr h∈ℋ [ k ⋀ i=1 h(xi ) = yi ] = 1 mk