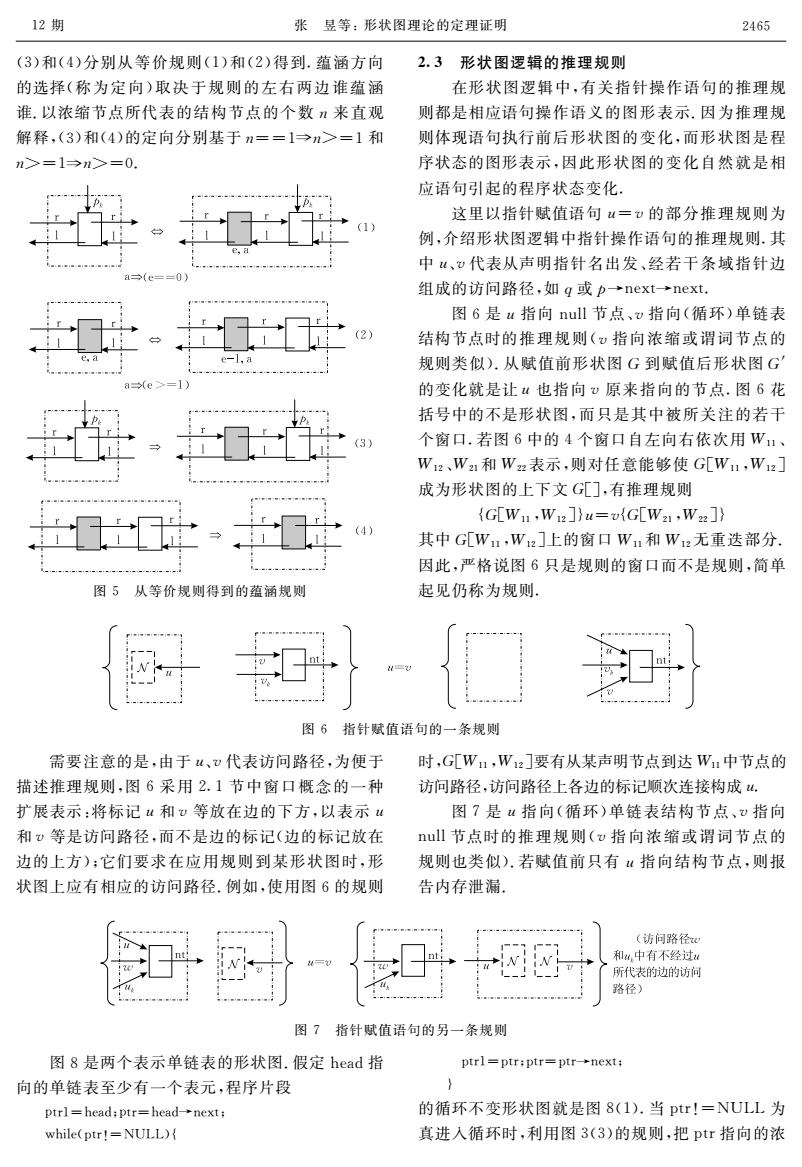
12期 张昱等:形状图理论的定理证明 2465 (3)和(4)分别从等价规则(1)和(2)得到.蕴涵方向 2.3形状图逻辑的推理规则 的选择(称为定向)取决于规则的左右两边谁蕴涵 在形状图逻辑中,有关指针操作语句的推理规 谁.以浓缩节点所代表的结构节点的个数n来直观 则都是相应语句操作语义的图形表示.因为推理规 解释,(3)和(4)的定向分别基于n==1→n>=1和 则体现语句执行前后形状图的变化,而形状图是程 n>=1→n>=0. 序状态的图形表示,因此形状图的变化自然就是相 应语句引起的程序状态变化. 这里以指针赋值语句u=?的部分推理规则为 1) 例,介绍形状图逻辑中指针操作语句的推理规则.其 中“、v代表从声明指针名出发、经若干条域指针边 组成的访问路径,如q或p→next->next. 图6是u指向null节点、v指向(循环)单链表 2) 结构节点时的推理规则(v指向浓缩或谓词节点的 规则类似).从赋值前形状图G到赋值后形状图G 的变化就是让也指向v原来指向的节点.图6花 括号中的不是形状图,而只是其中被所关注的若干 个窗口.若图6中的4个窗口自左向右依次用W1、 W2、W!和W2表示,则对任意能够使G[W11,W1z] 成为形状图的上下文G汇],有推理规则 {G[W1,W12]}u={G[W21,Wz2]} 其中G[W1,W2]上的窗口W1和W12无重迭部分。 因此,严格说图6只是规则的窗口而不是规则,简单 图5从等价规则得到的蕴规则 起见仍称为规则 图6指针赋值语句的一条规侧 需要注意的是,由于u、v代表访问路径,为便于 时,G[W1,W12]要有从某声明节点到达W,中节点的 描述推理规则,图6采用2.1节中窗口概念的一种 访问路径,访问路径上各边的标记顺次连接构成u. 扩展表示:将标记u和v等放在边的下方,以表示u 图7是“指向(循环)单链表结构节点、指向 和v等是访问路径,而不是边的标记(边的标记放在 null节点时的推理规则(v指向浓缩或谓词节点的 边的上方):它们要求在应用规则到某形状图时,形 规则也类似).若赋值前只有指向结构节点,则报 状图上应有相应的访问路径.例如,使用图6的规则 告内存泄漏, (访问路径 和4中有不经过u 所代表的边的访问 路径) 图7指针赋值语句的另一条规则 图8是两个表示单链表的形状图.假定head指 ptrl=ptr:ptr=ptr-next: 向的单链表至少有一个表元,程序片段 ptrl=head:ptr=head-next: 的循环不变形状图就是图8(1).当ptr!=NULL为 while(ptr!=NULL){ 真进入循环时,利用图3(3)的规则,把ptr指向的浓
(3)和(4)分别从等价规则(1)和(2)得到.蕴涵方向 的选择(称为定向)取决于规则的左右两边谁蕴涵 谁.以浓缩节点所代表的结构节点的个数狀来直观 解释,(3)和(4)的定向分别基于狀==1狀>=1和 狀>=1狀>=0. 图5从等价规则得到的蕴涵规则 23形状图逻辑的推理规则 在形状图逻辑中,有关指针操作语句的推理规 则都是相应语句操作语义的图形表示.因为推理规 则体现语句执行前后形状图的变化,而形状图是程 序状态的图形表示,因此形状图的变化自然就是相 应语句引起的程序状态变化. 这里以指针赋值语句狌=狏的部分推理规则为 例,介绍形状图逻辑中指针操作语句的推理规则.其 中狌、狏代表从声明指针名出发、经若干条域指针边 组成的访问路径,如狇或狆→next→next. 图6是狌指向null节点、狏指向(循环)单链表 结构节点时的推理规则(狏指向浓缩或谓词节点的 规则类似).从赋值前形状图犌到赋值后形状图犌′ 的变化就是让狌也指向狏原来指向的节点.图6花 括号中的不是形状图,而只是其中被所关注的若干 个窗口.若图6中的4个窗口自左向右依次用犠11、 犠12、犠21和犠22表示,则对任意能够使犌[犠11,犠12] 成为形状图的上下文犌[],有推理规则 {犌[犠11,犠12]}狌=狏{犌[犠21,犠22]} 其中犌[犠11,犠12]上的窗口犠11和犠12无重迭部分. 因此,严格说图6只是规则的窗口而不是规则,简单 起见仍称为规则. 图6指针赋值语句的一条规则 需要注意的是,由于狌、狏代表访问路径,为便于 描述推理规则,图6采用2.1节中窗口概念的一种 扩展表示:将标记狌和狏等放在边的下方,以表示狌 和狏等是访问路径,而不是边的标记(边的标记放在 边的上方);它们要求在应用规则到某形状图时,形 状图上应有相应的访问路径.例如,使用图6的规则 时,犌[犠11,犠12]要有从某声明节点到达犠11中节点的 访问路径,访问路径上各边的标记顺次连接构成狌. 图7是狌指向(循环)单链表结构节点、狏指向 null节点时的推理规则(狏指向浓缩或谓词节点的 规则也类似).若赋值前只有狌指向结构节点,则报 告内存泄漏. 图7指针赋值语句的另一条规则 图8是两个表示单链表的形状图.假定head指 向的单链表至少有一个表元,程序片段 ptr1=head;ptr=head→next; while(ptr!=NULL){ ptr1=ptr;ptr=ptr→next; } 的循环不变形状图就是图8(1).当ptr!=NULL为 真进入循环时,利用图3(3)的规则,把ptr指向的浓 12期 张昱等:形状图理论的定理证明 2465

2466 女 算 学 报 2016年 缩节点展开成两种情况,其一与ptr!=NULL矛 形状图等价规则限制为单向后得到的蕴涵规则 盾被略去,另一种情况就是图8(2)的形状图.把语 就是一条形状图重写规则.一组形状图重写规则构 句ptrl=ptr当作语句序列dummy=ptr;ptrl= 成一个形状图重写系统.不能用该系统的规则再进 NULL:ptrl=dummy:dummy=NULL,按图6和 行归约的形状图称为最简形状图.不存在无穷归约 图7的规则逐步修改图8(2),其中dummy是初值 序列的系统称为具有终止性的系统.可以参照项重 为NULL的虚拟局部指针变量.引入dummy主要 写系统继续定义系统的临界对(critical pair)、局部 是为了避免为某些特殊的指针赋值情况设计复杂的 合流性和合流性, 专用规则,见文献[10]的3.1节.对ptr=ptr--next 仿照Knuth-Bendix完备化过程),可以把文 也继续用类似的方法修改形状图,再把得到的形状 献[10]中2.3节的等价规则集变换成一个与之等价 图用类似图3(3)的规则,把ptr1原先指向的结构节 并且终止与合流的形状图重写系统R 点逆向折叠进左边的浓缩节点,得到图8(1). 下面先以一个简单的项重写系统为例来熟悉项 重写系统的一些概念,然后说明项重写和形状图重 写之间的主要异同.例如,代数等式 x十0=x,x十(一x)=0,(x十y)十之=x十(y十) nex 是属于包含0、加和一元减的自然数等式系统中的 等式,把它们从左到右定向,得到3条重写规则 x+0→x,x+(-x)→0,(x+y)+2→x+(y+之) 项x+(y+(一y)的子项y+(一y)与第2条规则 的左部匹配,因此x十(y+(一y)可用第2条规则 重写成x十0,再依据第1条规则重写为x.不难证 (2) 明这3条规则构成的重写系统是终止的. 图8形状图的两个例子 要证明合流性,需要考察临界对.第3条规则左 部的子项x十y和该规则左部(x'+y)+之'(加撇号 3形状图理论的判定方法 以便区别)合一,得到临界对 ((x'+y')+(+),(x'+(y+之'))+》 形状图的等价推理规则集由文献[10]中2.3节的 该临界对中的两个项都能归约到x'十(y'十(z'十z)) 形状图等价规则(不包括那些推导形状图析取G1VG2 可以类似地计算该重写系统的其它临界对并证明每 的规则,例如本文图3(3))和任何等价推理系统都 一临界对中的两个项都能归约到同一个项,所以该 有的自反、对称和传递规则组成.该规则集可用来证 系统具有局部合流性,再由终止性可得该系统具有 明形状图之间的等价性, 合流性。 若等价形状图的集合E是封闭于可证明的,即 在上述项重写系统中,规则的左部和右部都是 项,被重写的也是项.而形状图系统与项重写系统相 G1台G2蕴涵G台G2∈£,则把£叫做形状图的一 比,最大的区别是:规则的左部和右部都是窗口,被 个语法等价理论.类似地可以定义形状图相应的语 重写的是形状图.产生该区别的根源在于形状图是 义等价理论,即=G台G2蕴涵G1台G2∈C.由文献 二维的.基于同样的原因,合一和匹配的描述也有区 [10]中2.4节关于等价规则的性质定理,不难证明 别.但是两个系统的本质概念和方法是一致的, £G1台G2当且仅当£=G,台G2.类似地根据形状图 下面先给出节点相同和形状图相同的定义 的蕴涵规则,可以定义形状图的语法蕴涵理论和语义 定义1.节点1和2若满足下面两个条件,则 蕴涵理论及证明G1→G2当且仅当卡G,→G2: 称m1和n2相同: 本节介绍形状图的重写系统和这两种理论的判 (1)1和2是同类节点,并且若都是声明节点、 定方法。 结构节点或浓缩节点,则有同样的出边及其标记;若 3.1形状图的等价重写系统 都是谓词节点,则谓词名相同. 形状图的等价重写系统可比照代数项的重写系 (2)若1和2是同类浓缩节点或谓词节点,且 统[]来讨论.它用于形状分析和验证过程中对形状 分别带e1与a1和e2与a2,则必须满足(e1==e2A 图进行等价化简. a1)→a2并且(e1==e2∧a2)→a1.其中,无约束浓缩
缩节点展开成两种情况,其一与ptr!=NULL矛 盾被略去,另一种情况就是图8(2)的形状图.把语 句ptr1=ptr当作语句序列dummy=ptr;ptr1= NULL;ptr1=dummy;dummy=NULL,按图6和 图7的规则逐步修改图8(2),其中dummy是初值 为NULL的虚拟局部指针变量.引入dummy主要 是为了避免为某些特殊的指针赋值情况设计复杂的 专用规则,见文献[10]的3.1节.对ptr=ptr→next 也继续用类似的方法修改形状图,再把得到的形状 图用类似图3(3)的规则,把ptr1原先指向的结构节 点逆向折叠进左边的浓缩节点,得到图8(1). 图8形状图的两个例子 3形状图理论的判定方法 形状图的等价推理规则集由文献[10]中2.3节的 形状图等价规则(不包括那些推导形状图析取犌1∨犌2 的规则,例如本文图3(3))和任何等价推理系统都 有的自反、对称和传递规则组成.该规则集可用来证 明形状图之间的等价性. 若等价形状图的集合犈是封闭于可证明的,即 ! "犌1犌2蕴涵犌1犌2∈!,则把!叫做形状图的一 个语法等价理论.类似地可以定义形状图相应的语 义等价理论,即! #犌1犌2蕴涵犌1犌2∈!.由文献 [10]中2.4节关于等价规则的性质定理,不难证明 ! "犌1犌2当且仅当! #犌1犌2.类似地根据形状图 的蕴涵规则,可以定义形状图的语法蕴涵理论和语义 蕴涵理论及证明! "犌1犌2当且仅当! #犌1犌2. 本节介绍形状图的重写系统和这两种理论的判 定方法. 31形状图的等价重写系统 形状图的等价重写系统可比照代数项的重写系 统[12]来讨论.它用于形状分析和验证过程中对形状 图进行等价化简. 形状图等价规则限制为单向后得到的蕴涵规则 就是一条形状图重写规则.一组形状图重写规则构 成一个形状图重写系统.不能用该系统的规则再进 行归约的形状图称为最简形状图.不存在无穷归约 序列的系统称为具有终止性的系统.可以参照项重 写系统继续定义系统的临界对(criticalpair)、局部 合流性和合流性. 仿照KnuthBendix完备化过程[13],可以把文 献[10]中2.3节的等价规则集变换成一个与之等价 并且终止与合流的形状图重写系统$. 下面先以一个简单的项重写系统为例来熟悉项 重写系统的一些概念,然后说明项重写和形状图重 写之间的主要异同.例如,代数等式 狓+0=狓,狓+(-狓)=0,(狓+狔)+狕=狓+(狔+狕) 是属于包含0、加和一元减的自然数等式系统中的 等式,把它们从左到右定向,得到3条重写规则 狓+0→狓,狓+(-狓)→0,(狓+狔)+狕→狓+(狔+狕) 项狓+(狔+(-狔))的子项狔+(-狔)与第2条规则 的左部匹配,因此狓+(狔+(-狔))可用第2条规则 重写成狓+0,再依据第1条规则重写为狓.不难证 明这3条规则构成的重写系统是终止的. 要证明合流性,需要考察临界对.第3条规则左 部的子项狓+狔和该规则左部(狓′+狔′)+狕′(加撇号 以便区别)合一,得到临界对 〈(狓′+狔′)+(狕′+狕),(狓′+(狔′+狕′))+狕〉 该临界对中的两个项都能归约到狓′+(狔′+(狕′+狕)). 可以类似地计算该重写系统的其它临界对并证明每 一临界对中的两个项都能归约到同一个项,所以该 系统具有局部合流性.再由终止性可得该系统具有 合流性.在上述项重写系统中,规则的左部和右部都是 项,被重写的也是项.而形状图系统与项重写系统相 比,最大的区别是:规则的左部和右部都是窗口,被 重写的是形状图.产生该区别的根源在于形状图是 二维的.基于同样的原因,合一和匹配的描述也有区 别.但是两个系统的本质概念和方法是一致的. 下面先给出节点相同和形状图相同的定义. 定义1.节点狀1和狀2若满足下面两个条件,则 称狀1和狀2相同: (1)狀1和狀2是同类节点,并且若都是声明节点、 结构节点或浓缩节点,则有同样的出边及其标记;若 都是谓词节点,则谓词名相同. (2)若狀1和狀2是同类浓缩节点或谓词节点,且 分别带e1与a1和e2与a2,则必须满足(e1==e2∧ a1)a2并且(e1==e2∧a2)a1.其中,无约束浓缩 2466 计 算 机 学 报 2016年