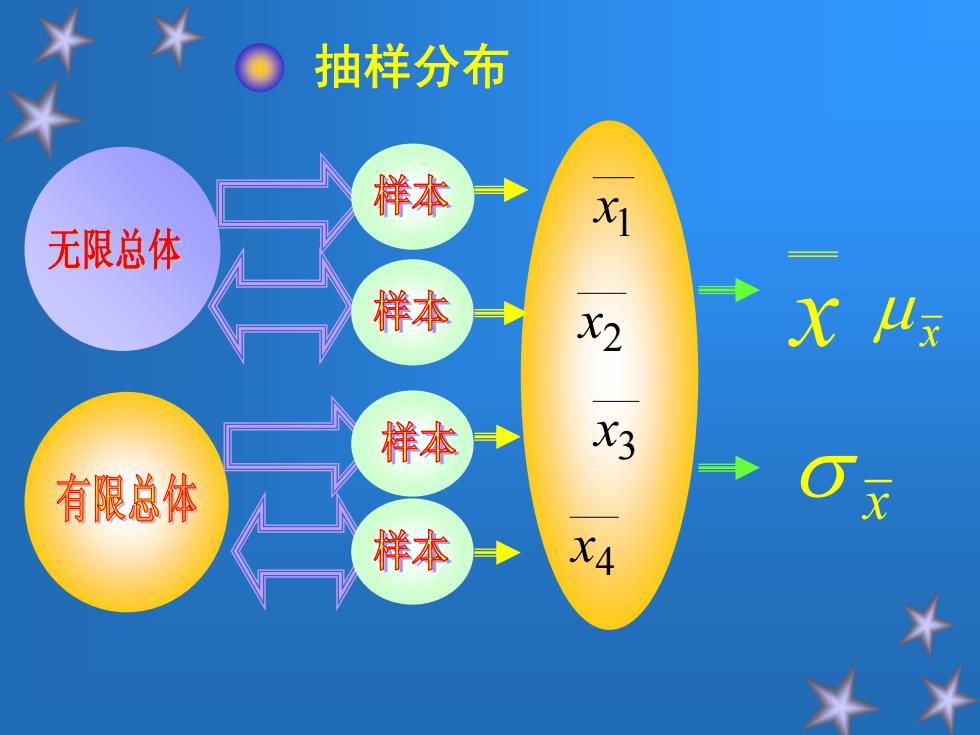
抽样分布 样本 无限总体 样本 X Mx 样本 有限总体 x 样本 XA
抽样分布 1 x 2 x 3 x 4 x x x x

一 般意义上说,抽样分布是指样本统计量的概率 分布。 ● 说的具体一些,某个样本统计量的抽样分布,从 理论上说就是在重复选取容量为n的样本时,由每 一个样本算出的该统计量数值的相对频数分布。 ● 由于现实中我们不可能将所有的样本都抽出来, 因此,统计量的抽样分布实际上是一种理论分布
一般意义上说,抽样分布是指样本统计量的概率 一般意义上说,抽样分布是指样本统计量的概率 分布。 说的具体一些,某个样本统计量的抽样分布,从 说的具体一些,某个样本统计量的抽样分布,从 理论上说就是在重复选取容量为 理论上说就是在重复选取容量为 n的样本时,由每 的样本时,由每 一个样本算出的该统计量数值的相对频数分布。 一个样本算出的该统计量数值的相对频数分布。 由于现实中我们不可能将所有的样本都抽出来, 由于现实中我们不可能将所有的样本都抽出来, 因此,统计量的抽样分布实际上是一种理论分布。 统计量的抽样分布实际上是一种理论分布

统计量与抽样分布 样本平均值X下= ΣX 统计量:即样本特征数。 如: 样本方差 S2=- xx-I 抽样分布:某一统计量所有可能的样本的取值形成 的分布。 质 0≤P(X) ≤I 性 平均值E(X) P (X) 数字特征 方差Ex-E(X)] 抽样分布的标准差就是推断的抽样误差
统计量与抽样分布 统计量与抽样分布 •统计量 :即样本特征数 。 样本平均值 样本方差 如 : n X X i 2 2)( 1 1 XX n S i •抽样分布:某一统计量所有可能的样本的取值形成 某一统计量所有可能的样本的取值形成 的分布。 性 质 数字特征 0 ≤ P ( X i ) 1 ∑ P ( X i )=1 平均值 E ( X ) 方差E[x-E(x)] 2 抽样分布的标准差就是推断的 抽样分布的标准差就是推断的抽样误差

4.1.2 样本平均数的抽样分布 设有一个任意总体(,σ2),将此总体称为原总 体。现从这个总体中随机抽取含量为的样本,样 本平均数记为x 从原总体中可抽出Nn个含量为n的样本(有限总体 放回式抽样)。这些样本的平均数不尽相同,与原 总体平均数相比表现出不同程度的差异。这种差 异是由随机抽样造成的,称为抽样误差
设有一个任意总体 (μ,σ2),将此总体称为原总 体。现从这个总体中随机抽取含量为n的样本,样 本平均数记为 。 从原总体中可抽出Nn个含量为n的样本(有限总体 放回式抽样)。这些样本的平均数不尽相同,与原 总体平均数μ相比表现出不同程度的差异。这种差 异是由随机抽样造成的,称为抽样误差。 x 4.1.2 样本平均数的抽样分布
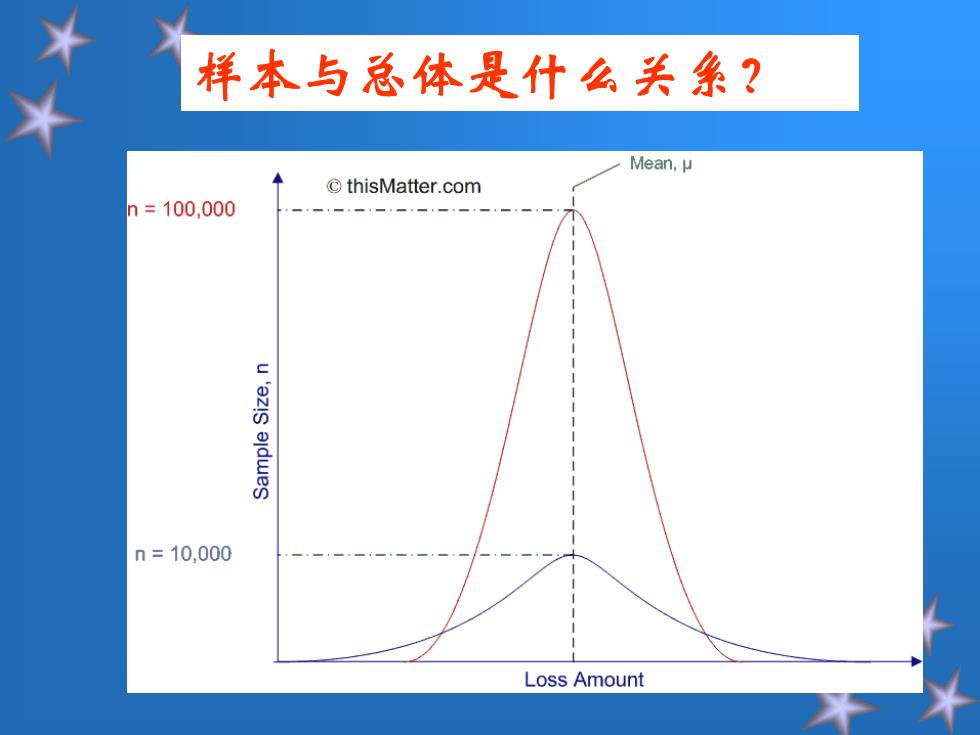
样本与总体是什么关系? Mean,μ ©thisMatter.com h=100,000 n=10,000 Loss Amount
样本与总体是什么关系?