
11 凸轮机构工作可靠、布局方便,特别是它能使从动杆实 现任意的运动规律,因而在裹包机中应用广泛。下面结合具 体应用,着重讨论选择从动系统的运动形式设计问题,而 确定参数这个问题不作为重点。 (一)从动系统的形式 选择从动系统,要求构件数目少、传动效率高、结构简 单。为此,应尽量采用由凸轮直接驱动执行构件的方案。但 这不是经常能实现的。对设计裹包机来说,有时还必须通过 中间传动件,如执行构件远离凸轮轴、摆动执行构件的角位 移过大、或者为减小凸轮几何尺寸以及便于布局等可考虑 如下四种中间传动形式。 上一页 主页 下一页
11 凸轮机构工作可靠、布局方便,特别是它能使从动杆实 现任意的运动规律,因而在裹包机中应用广泛。下面结合具 体应用,着重讨论选择从动系统的运动形式设计问题,而 确定参数这个问题不作为重点。 (一)从动系统的形式 选择从动系统,要求构件数目少、传动效率高、结构简 单。为此,应尽量采用由凸轮直接驱动执行构件的方案。但 这不是经常能实现的。对设计裹包机来说,有时还必须通过 中间传动件,如执行构件远离凸轮轴、摆动执行构件的角位 移过大、或者为减小凸轮几何尺寸以及便于布局等可考虑 如下四种中间传动形式。 上一页 主页 下一页
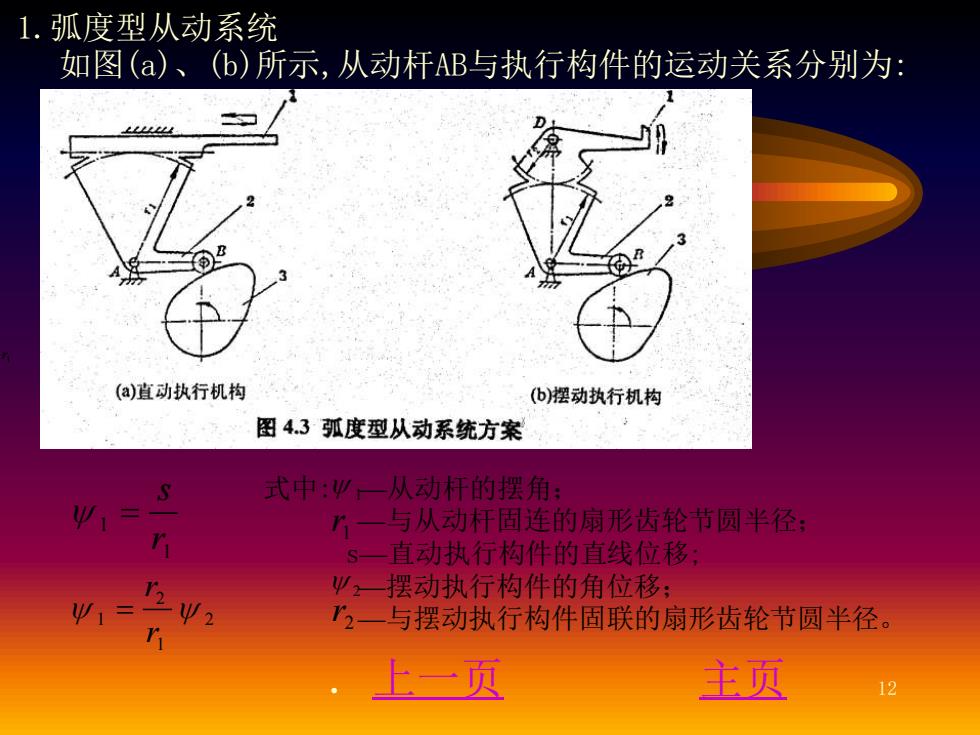
. 上一页 主页 12 1.弧度型从动系统 如图(a)、(b)所示,从动杆AB与执行构件的运动关系分别为: 1 1 = s r 1 2 1 = 2 r r 式中: —从动杆的摆角; —与从动杆固连的扇形齿轮节圆半径; s—直动执行构件的直线位移; —摆动执行构件的角位移; —与摆动执行构件固联的扇形齿轮节圆半径。 1 r1 2 r2 r1
. 上一页 主页 12 1.弧度型从动系统 如图(a)、(b)所示,从动杆AB与执行构件的运动关系分别为: 1 1 = s r 1 2 1 = 2 r r 式中: —从动杆的摆角; —与从动杆固连的扇形齿轮节圆半径; s—直动执行构件的直线位移; —摆动执行构件的角位移; —与摆动执行构件固联的扇形齿轮节圆半径。 1 r1 2 r2 r1
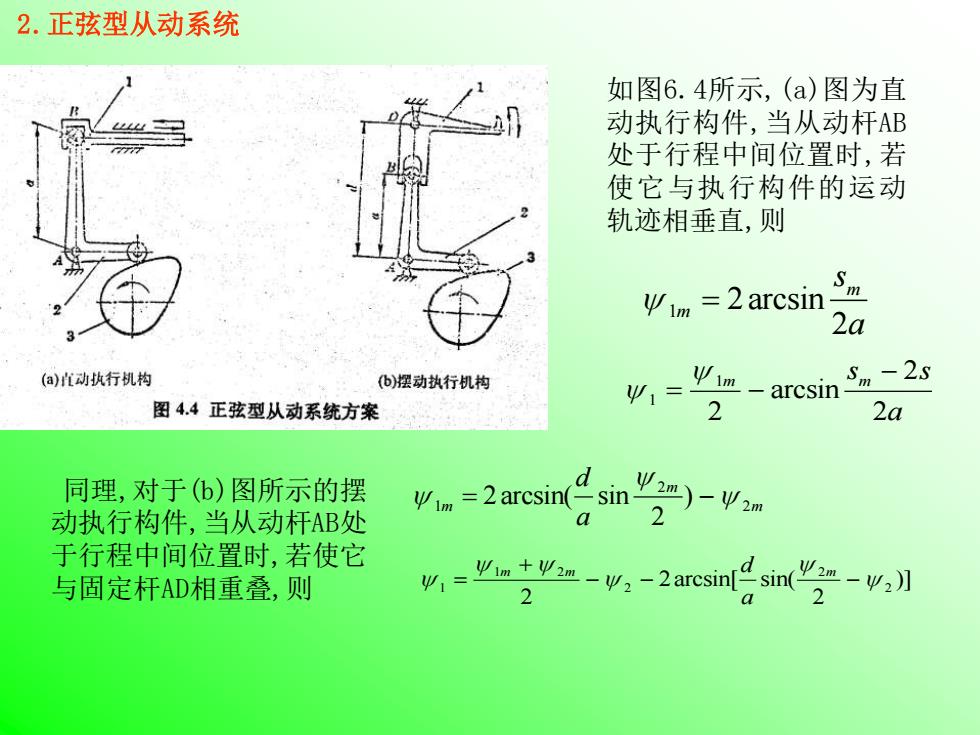
2.正弦型从动系统 1 2 2 m m s a = arcsin 1 1 2 2 2 = − m s m − s a arcsin 1 2 2 2 2 m m m d a = arcsin( sin ) − 1 1 2 2 2 2 2 2 2 = + − − − m m d m a arcsin[ sin( )] 如图6.4所示,(a)图为直 动执行构件,当从动杆AB 处于行程中间位置时,若 使它与执行构件的运动 轨迹相垂直,则 同理,对于(b)图所示的摆 动执行构件,当从动杆AB处 于行程中间位置时,若使它 与固定杆AD相重叠,则
2.正弦型从动系统 1 2 2 m m s a = arcsin 1 1 2 2 2 = − m s m − s a arcsin 1 2 2 2 2 m m m d a = arcsin( sin ) − 1 1 2 2 2 2 2 2 2 = + − − − m m d m a arcsin[ sin( )] 如图6.4所示,(a)图为直 动执行构件,当从动杆AB 处于行程中间位置时,若 使它与执行构件的运动 轨迹相垂直,则 同理,对于(b)图所示的摆 动执行构件,当从动杆AB处 于行程中间位置时,若使它 与固定杆AD相重叠,则
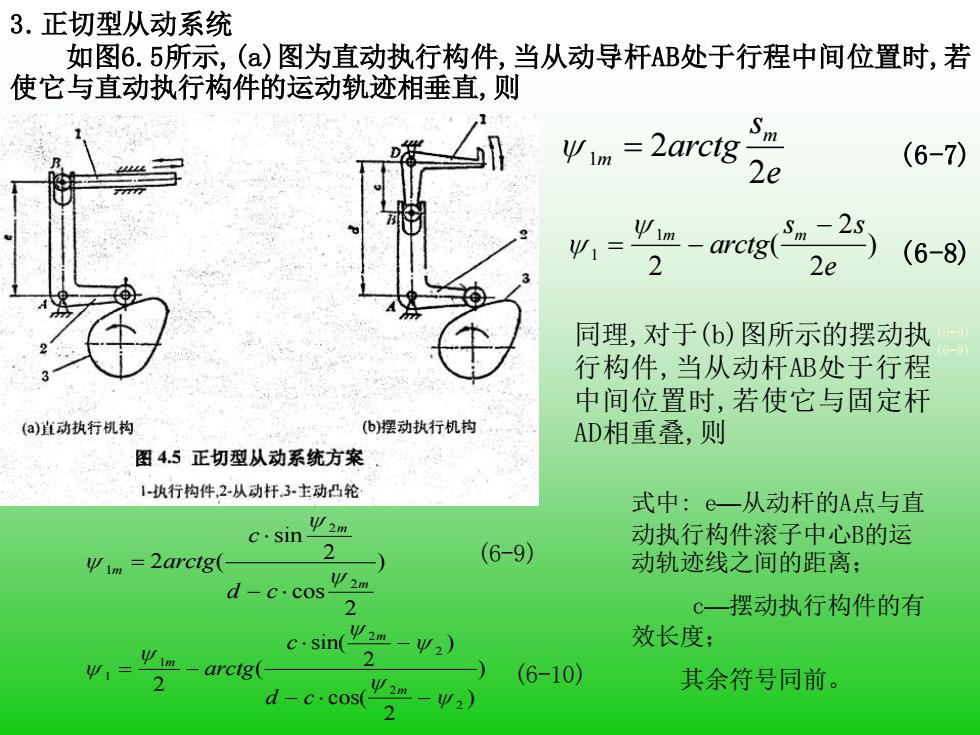
3.正切型从动系统 如图6.5所示,(a)图为直动执行构件,当从动导杆AB处于行程中间位置时,若 使它与直动执行构件的运动轨迹相垂直,则 (6-7) (6-8) 1 2 2 m m arctg s e = 1 1 2 2 2 = − m m − arctg s s e ( ) 同理,对于(b)图所示的摆动执 行构件,当从动杆AB处于行程 中间位置时,若使它与固定杆 AD相重叠,则 (6-9) 1 2 2 2 2 2 m m m arctg c d c = − ( sin cos ) 1 1 2 2 2 2 2 2 2 = − − − − m m m arctg c d c ( sin( ) cos( ) ) (6-9) (6-9) (6-10) 式中: e—从动杆的A点与直 动执行构件滚子中心B的运 动轨迹线之间的距离; c—摆动执行构件的有 效长度; 其余符号同前
3.正切型从动系统 如图6.5所示,(a)图为直动执行构件,当从动导杆AB处于行程中间位置时,若 使它与直动执行构件的运动轨迹相垂直,则 (6-7) (6-8) 1 2 2 m m arctg s e = 1 1 2 2 2 = − m m − arctg s s e ( ) 同理,对于(b)图所示的摆动执 行构件,当从动杆AB处于行程 中间位置时,若使它与固定杆 AD相重叠,则 (6-9) 1 2 2 2 2 2 m m m arctg c d c = − ( sin cos ) 1 1 2 2 2 2 2 2 2 = − − − − m m m arctg c d c ( sin( ) cos( ) ) (6-9) (6-9) (6-10) 式中: e—从动杆的A点与直 动执行构件滚子中心B的运 动轨迹线之间的距离; c—摆动执行构件的有 效长度; 其余符号同前
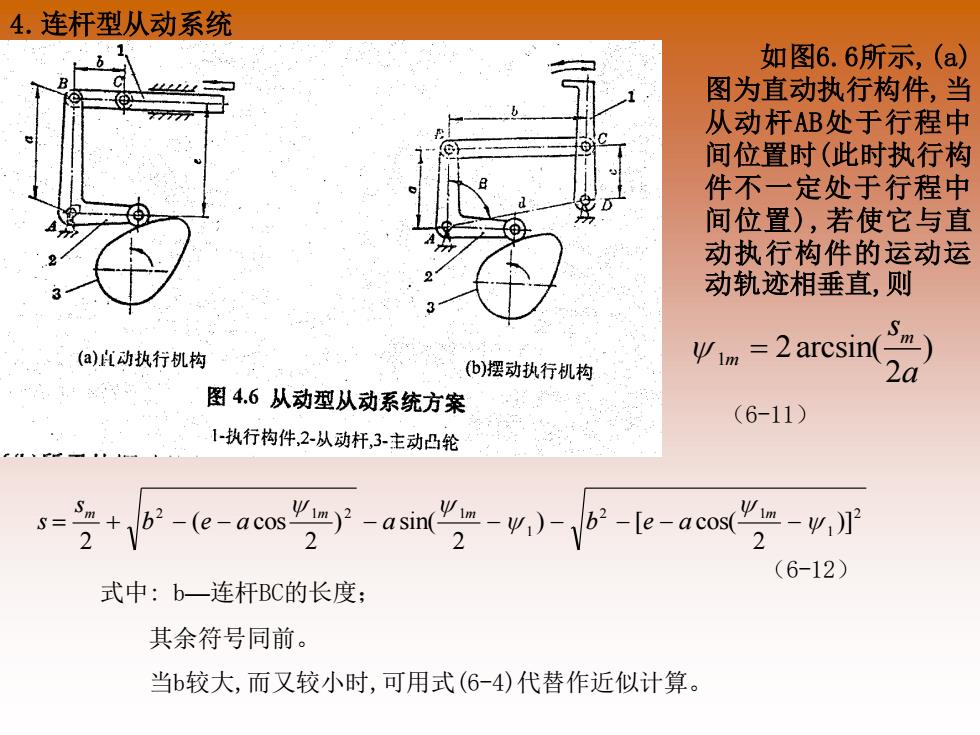
如图6.6所示,(a) 图为直动执行构件,当 从动杆AB处于行程中 间位置时(此时执行构 件不一定处于行程中 间位置),若使它与直 动执行构件的运动运 动轨迹相垂直,则 1 2 2 m m s a = arcsin( ) s s b e a a b e a m m m m = + − − − − − − − − 2 2 2 2 2 1 2 1 1 2 1 1 2 ( cos ) sin( ) [ cos( )] 4.连杆型从动系统 (6-11) 式中: b—连杆BC的长度; 其余符号同前。 当b较大,而又较小时,可用式(6-4)代替作近似计算。 (6-12)
如图6.6所示,(a) 图为直动执行构件,当 从动杆AB处于行程中 间位置时(此时执行构 件不一定处于行程中 间位置),若使它与直 动执行构件的运动运 动轨迹相垂直,则 1 2 2 m m s a = arcsin( ) s s b e a a b e a m m m m = + − − − − − − − − 2 2 2 2 2 1 2 1 1 2 1 1 2 ( cos ) sin( ) [ cos( )] 4.连杆型从动系统 (6-11) 式中: b—连杆BC的长度; 其余符号同前。 当b较大,而又较小时,可用式(6-4)代替作近似计算。 (6-12)